Applying Multiplication Properties

Overview
Lesson Overview
Students apply the multiplication property of equality to solve equations.
Key Concepts
In the previous lesson, students solved equations of the form x + p = q using the addition property of equality. In this lesson, they will solve equations of the form px = q using the multiplication property of equality. They will multiply or divide both sides of an equation by the same number to obtain an equivalent equation.
Since multiplication by a is equivalent to division by , students will see that they may also divide both sides of the equation by the same number to get an equivalent equation. Students will also apply this property to solving a particular kind of equation, a proportion.
Goals and Learning Objectives
- Use the multiplication property of equality to keep an equation balanced.
- Use the multiplication property of equality to solve equations of the form px = q for cases in which p, q, and x are all non-negative rational numbers.
- Use the multiplication property of equality to solve proportions.
Keep Balanced
Lesson Guide
Have students work with a partner to answer the two questions.
ELL: With this problem, demonstrate and verbally explain the problem step by step. Rephrase instructions to provide multiple opportunities for understanding. Give students the chance to restate their understanding.
Opening
Keep Balanced
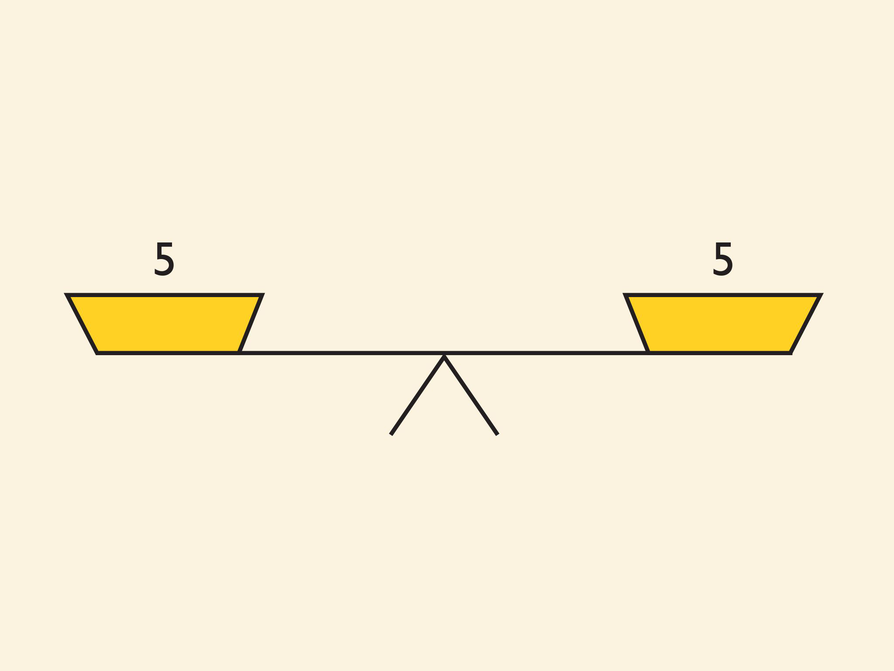
Look at the balance scale pictured here.
- What number can you multiply the number on each side of the scale by but still keep the scale balanced?
- Based on your new scale, what number can you divide both sides by to keep the scale balanced?
Solve for x
Lesson Guide
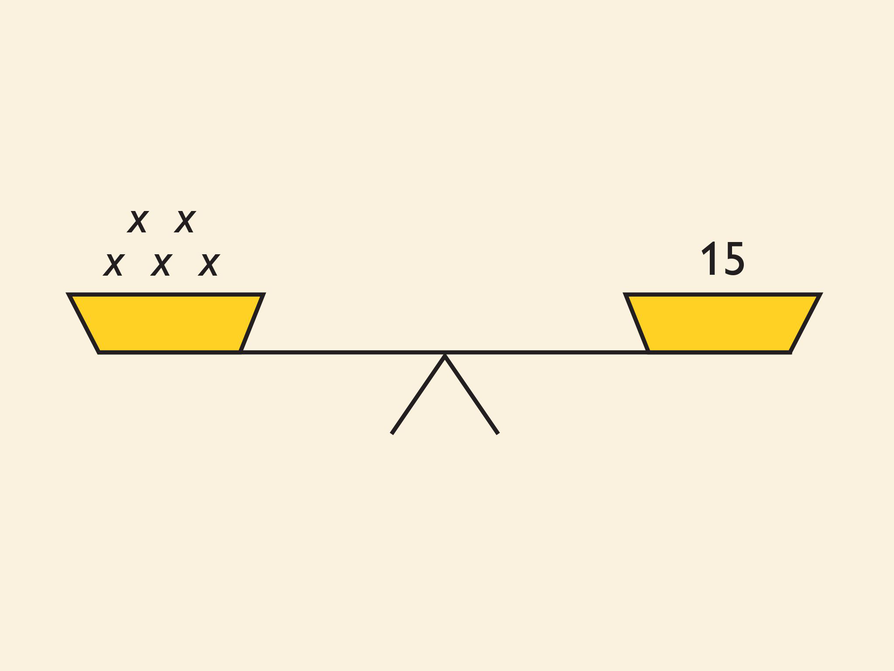
Have students work in pairs on writing and solving the equation 5x = 15.
Mathematics
The whole-group discussion that follows should result in students' understanding that the scale will remain balanced if both sides of the equation are multiplied by the same number (any number) or divided by the same number (any number). This is known as the multiplication property of equality .
If each side of the scale is divided by 5, then x remains on the left and 3 remains on the right, and the scale is still balanced.
So, 5x = 15 is equivalent to x = 3, and the solution to both equations is 3.
Opening
Solve for x
Look at the balance scale.
- Write an equation that represents the balance scale.
- Can you multiply or divide both sides of the equation by some number in order to find the value of x that makes the equation true?
- What is the solution?
- Substitute your solution for x in your equation to check your answer.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use the multiplication property of equality to solve equations.
Opening
Use the multiplication property of equality to solve equations.
Solve the Equations
Lesson Guide
Have students work in pairs on all problems and the presentation in Task 5. Make sure a variety of problems are chosen for the student presentations.
SWD: Consider the prerequisite skills for this task/skill. Students with disabilities may need direct instruction on and guided practice with simplifying fractions and decimals to complete this task.
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Listen for students who verbalize that as soon as x is by itself on one side and a number on the other side, they have the solution to the equation.
Mathematical Practice 7: Look for and make use of structure.
Look for students who understand how multiplication and division undo one another; students may talk about undoing "multiply by 5" by "divide by 5."
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Identify students who apply what they learned from solving one equation to solving the next.
Interventions
Student does not see how these equations are different from the equations in the previous lesson.
- What did you do to get just one x on the left?
- Why can't you subtract four x-variables from the right?
- How else can you go from four x-variables to one x? Think about the problem from the Opening.
For 4x = 24, student does not understand how to physically show dividing both sides.
- Think about dividing both sides by 4.
- How many x-variables will be on the left?
- What number will be on the right?
Student does not know how to find the solution using the multiplication property of equality.
- What does the multiplication property of equality mean?
- How did you use the addition property of equality? Can you apply that method to the multiplication property of equality?
- What is the opposite of multiplying?
Student is not sure he or she found the correct solution.
- Substitute your solution for x. Do you get a true equation?
ELL: When presenting the guiding questions in Interventions, be sure that ELLs can follow what you are saying. Provide written questions, and use a pace that is appropriate for non-English speakers. Discuss newly introduced vocabulary (e.g., multiplication property of equality) at a slower pace to ensure understanding and recollection of meaning.
Answers
- 4x = 24
=
x = 6
or
4x = 24
4x • = 24 •
x = 6
Check:
4 • 6 = 24
24 = 24
- x = 7
x • 2 = 7 • 2
x = 14
Check:
• 14 = 7
7 = 7
- 1.5x = 12
=
x = 8
Check:
1.5 • 8 = 12
12 = 12
Work Time
Solve the Equations
Multiplication property of equality: If you multiply both sides of an algebraic equation by the same number, except zero, or divide both sides of an algebraic equation by the same number, except zero, the equations will have the same solution.
Use the multiplication property of equality to solve each equation. Check your solution by substituting the solution into the original equation.
- 4x = 24
- x = 7
- 1.5x = 12
Hint:
What number can you multiply or divide by to get x by itself on one side of the equation?
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who use the multiplication property of equality to solve the equations. Watch for students who fail to perform the same operation on both sides of the equation.
Challenge Problem
Answers
- First subtract 8 from both sides.
3x + 8 – 8 = 15 – 8
3x = 7
Then divide both sides by 3.
3x ÷ 3 = 7 ÷ 3
x = 2.33
Work Time
Prepare a Presentation
Select one of the problems from Task 4.
- Explain how you used the multiplication property of equality to solve the equation.
- Explain how you checked your answer.
Challenge Problem
- How could you use both the addition and multiplication properties of equality to solve the equation 3x + 8 = 15?
Make Connections
Lesson Guide
As students give their presentations and discuss their solution processes, be sure the following points are covered:
- You have the solution to the equation when x is on one side and a number is on the other side. It does not matter whether the x is on the right or the left side.
- If x has been multiplied by a number, you can “undo” that by using the inverse operation. Multiplication and division are inverse operations.
- Even though the original equation and the new equation look different, they are equivalent. That means that they have the same solution.
- Dividing by a number and multiplying by its reciprocal give the same result. So, one student may solve 4x = 24 by dividing both sides by 4 and another may multiply both sides by ; both get the same result.
- Whenever you multiply or divide both sides of an equation by the same number, the new equation will be equivalent to the original equation. This is known as the multiplication property of equality.
The Challenge Problem requires that students use both the addition and the multiplication properties of equality. Allow students who attempted the problem to share their solutions. If no one attempted it, share this alternative solution:
Alternative Solution
| 3x + 8 = 15 | |
|---|---|
= | Multiplication property of equality |
+ = | |
x + − = − | Addition property of equality |
x = , or 2.33 |
Discuss with students which method they prefer: beginning with the addition property or beginning with the multiplication property.
SWD: Participating in a whole-class discussion can be intimidating for students with language-based learning vulnerabilities and/or learning challenges. Supports for students during this portion of the lesson include:
- Prompt students to discuss their ideas, the questions posed, and what has taken place during the lesson with a partner or small group before sharing out in the whole-class setting.
- Conference with individual students prior to the discussion to ascertain what they might be able to successfully contribute to the discussion. Encourage students to rehearse their contribution or to write notes as a reference for when they speak. This will support students with expressive language difficulties and/or students who are anxious or reluctant to participate in class discussions.
Teacher Demonstration
Explain to students that they will now learn how to record the steps in the equation solution. Write 5x = 35 on the board.
- What should you do to both sides of the equation to keep it balanced? (Answer: Divide both sides by 5 or multiply both sides by .)
- Show students how to record the division.
5x = 35
=
x = 7 - Show students how to record the multiplication.
5x = 35
• 5x = • 35
x = 7
- Have students substitute 7 into the original equation to show that it is the correct solution.
5x = 35
5 ⋅ 7 = 35
35 = 35
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ methods for solving equations using the multiplication property of equality.
Hint:
As your classmates present, ask questions such as:
- How did you know whether to divide or multiply to solve the equation?
- Why do you need to do the same thing on both sides of an equation?
- What could you do if you checked your solution and found that your solution was incorrect?
Apply the Property
Lesson Guide
Pair up students to solve the equations. Have students who are struggling with fraction and decimal operations work with students who have mastered these skills. Remind students to think about inverse operations when solving the equations and to record their steps.
When students have completed the problems, have volunteers present their solutions. Try to find both a student who used multiplication and a student who used division for each equation. When discussing , ask students: What special name can you give this equation?
Discuss how this equation is a proportion and how the multiplication property of equality can help students solve proportions. Invite volunteers to share other ways they have learned to solve the proportion .
SWD: An alternative to having students describe the entire process would be to have them write justifications for each step next to their equations. Make sure they reference the addition property of equality and the multiplication property of equality.
Answers
- 5x = 65
=
x = 13
or
5x = 65
5x • = 65 •
x = 13
Check:
5 • 13 = 65
65 = 65
- x = 7
x • = 7 •
x = or x = 32
Check:
• = 7
= 7
7 = 7
- 7.2 = 4x
=
x = 1.8
or
7.2 = 4x
• = 4x •
x = or x = 1
Check:
7.2 = 4 • 1.8
7.2 = 7.2
or
7.2 = 4 •
7 = 7
- =
• 4 = • 4
x = 2
Check:
=
=
Work Time
Apply the Property
Solve the equations using the multiplication property of equality. Show each step of your work, and check your solutions.
- 5 = 65
- x = 7
- 7.2 = 4x
- =
The Multiplication Property of Equality
A Possible Summary
Multiplying or dividing both sides of an equation by the same number will result in an equivalent equation. This is called the multiplication property of equality. For example, 12 = 12. If you multiply both sides by 2, you get another true equation, 24 = 24. If you begin with 12 = 12 and divide both sides by 2, you get the true equation 6 = 6.
To solve 5x = 65, you divide both sides by 5 (or multiply both sides by ), so 5x • 5 = 65 • 5, or x = 13.
To solve 12x = 9, you multiply both sides by 2 (or divide both sides by ), so 12x ⋅ 2 = 9 ⋅ 2, or
x = 18.
To solve = 39, you multiply both sides by 6, so ⋅ 6 = 39 ⋅ 6, or x = 234.
Formative Assessment
Summary of the Math: The Multiplication Property of Equality
Write a summary about the multiplication property of equality and give an example.
Hint:
Check your summary:
- Do you define the multiplication property of equality and provide an example of how it works? (Use a simple equation such as 12=12.)
- Do you explain how to use the multiplication property of equality to solve an equation such as 5x=19?
- Do you explain how to use the multiplication property of equality to solve an equation such as 12x=9?
- Do you explain how to use the multiplication property of equality to solve a proportion such as x6 = 63 ?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to learn what students still don't understand about using the multiplication property of equality to solve equations.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I still don’t understand about using the multiplication property of equality to solve equations is …