Comparing Surface Area & Volume

Overview
Lesson Overview
Students make two different rectangular prisms by folding two 8 in. by 11 in. sheets of paper in different ways. Then students use reasoning to compare the total areas of the faces of the two prisms (i.e., their surface areas). Students also predict how the amounts of space inside the prisms (i.e., their volumes) compare. They will check their predictions in Lesson 6.
Key Concepts
Students compare the total area of the faces (i.e., surface area) of one rectangular prism to the total area of the faces of another prism. Students make predictions about which prism has the greater amount of space inside (i.e., the greater volume). Students do not compute actual surface areas or volumes. This exploration helps pave the way for a more formal study of volume in Lesson 6 and a more formal study of surface area in Lesson 7.
Goals and Learning Objectives
- Explore how the surface areas and volumes of two different prisms made from the same-sized sheet of paper compare.
Divide a Paper Into Fourths
Lesson Guide
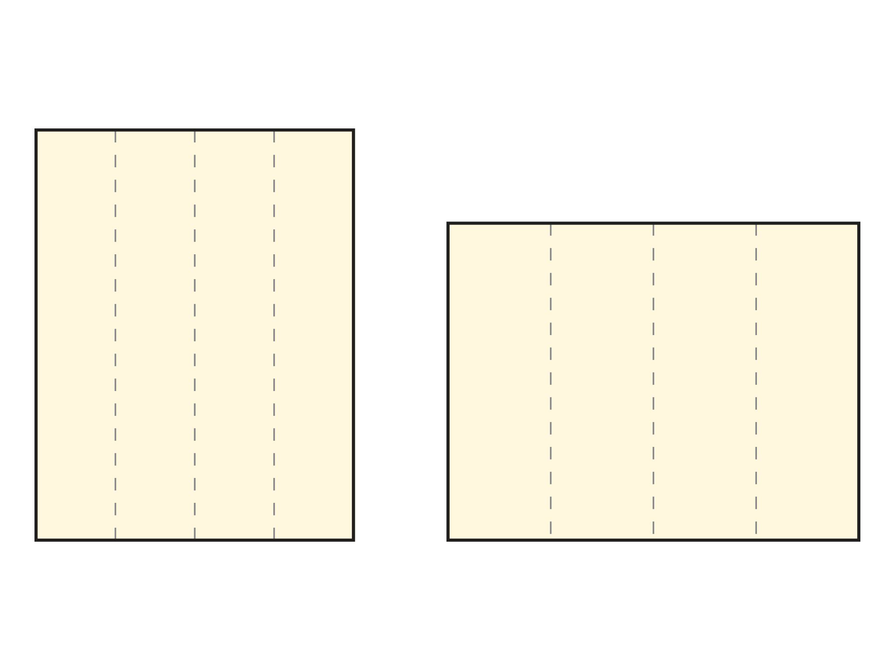
Have students work in pairs to create the two prisms. Each pair of students will need two sheets of 8 by 11 in. paper and some tape. Students can divide the sheets into fourths by folding them in half and then in half again.
Opening
Divide a Paper Into Fourths
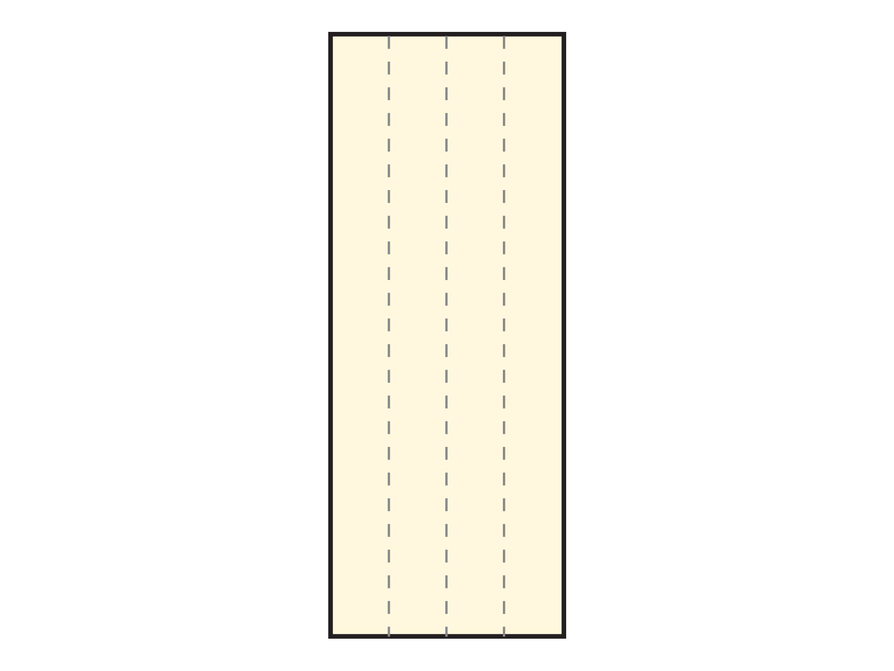
Start with two 8 by 11 in. sheets of paper.
- Using a ruler, divide each sheet into fourths as shown in the diagram.
- Draw lines to mark the divisions.
Make Paper Prisms
Lesson Guide
Check to see if students are assembling their prisms correctly. Partners should discuss how the prisms compare.
SWD: Students with motor difficulties may need support with the physical task of making the two prisms. Make sure that those students are partnered with another student who can assist them in completing this task.
Opening
Make Paper Prisms
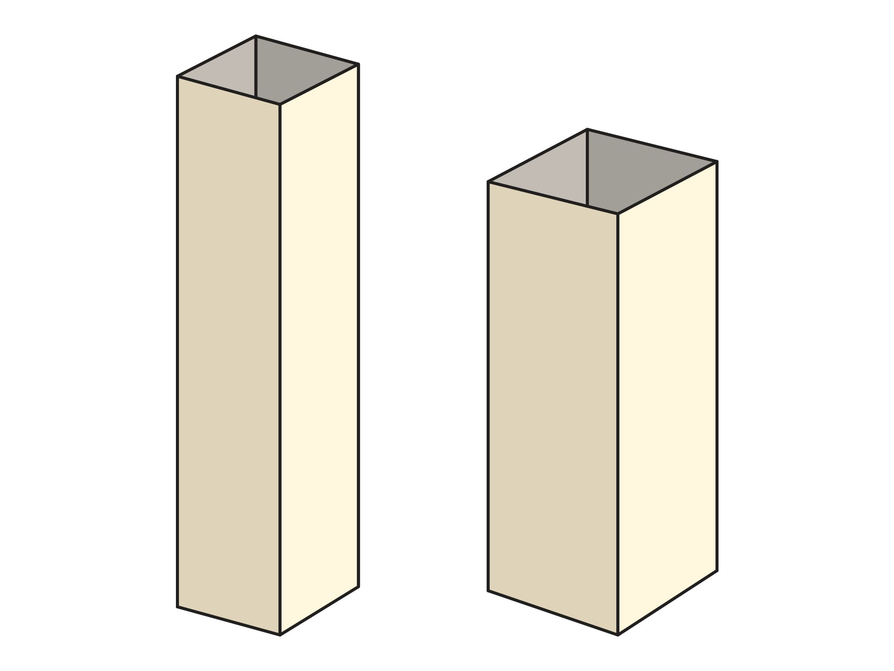
- Fold each sheet of paper along the division lines to form two rectangular prisms that are open at the top and the bottom.
- Discuss with your partner how the two prisms compare.
Math Mission
Lesson Guide
Discuss the Math Mission. Be sure students understand what the “surface area and volume” of a prism refers to.
ELL: This problem is a good opportunity for students to develop and use their academic and mathematical vocabulary around surface area and volume. Encourage students to share their thinking with a partner. Make sure all students know the definitions for surface area and volume. Consider posting these definitions on the word wall or on anchor charts as a reference during this unit.
Opening
Explore the surface area and volume of prisms.
Surface Area of Four Sides
Lesson Guide
Have partners work on the problems.
SWD: It will be difficult for some students to understand how differently-shaped objects can have the same lateral surface area. Help students make connections between the lateral area and using the same-sized sheet of paper to construct.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students should be clear about what is meant by the surface area of all (six faces) or part (e.g., four faces) of a rectangular prism. Likewise, they should be clear about what is meant by the volume of a rectangular prism. Knowing the meaning of these two terms will allow students to make sense of the math problems presented in this lesson.
Interventions
Student has difficulty comparing the total surface area of the four sides of each prism.
- Focus just on the four sides of the two prisms. Ignore the top and bottom for now.
- Remember that the two prisms are made from same-sized sheets of paper.
- How does the total surface area of the sides of the taller prism compare to the total surface area of the sides of the shorter prism?
Answers
- The total surface area of the four sides is the same for both prisms because both are made from the same-sized sheets of paper.
Work Time
Surface Area of Four Sides
Think about the four faces (sides) of the two paper prisms.
- Is the total surface area of these four faces the same or different for the two prisms?
- If it is different, which prism has the greater surface area?
Hint:
- What did you start with to form each prism?
- What is the area of each piece of paper? Have these areas changed?
Surface Area of Six Sides
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students should be clear about what is meant by the surface area of all (six faces) or part (e.g., four faces) of a rectangular prism. Likewise, they should be clear about what is meant by the volume of a rectangular prism. Knowing the meaning of these two terms will allow students to make sense of the math problems presented in this lesson.
Interventions
Student has difficulty comparing the total surface area of the four sides of each prism.
- Focus just on the four sides of the two prisms. Ignore the top and bottom for now.
- Remember that the two prisms are made from same-sized sheets of paper.
- How does the total surface area of the sides of the taller prism compare to the total surface area of the sides of the shorter prism?
Student has difficulty comparing the total surface area of all six faces of each prism.
- Just by looking, can you tell which prism has a top and bottom with the greater surface area?
Answers
- Yes, the total surface area of the six faces is different for the two prisms.
- The top and bottom faces of the shorter prism are larger than those of the taller prism. The combined surface area of the other four faces are the same for both prisms, so the total surface area of the six faces must be greater for the shorter prism.
Work Time
Surface Area of Six Sides
Suppose that you added a top and bottom to each prism.
- Is the total surface area of the six faces the same or different for the two prisms?
- If it is different, which prism has the greater area?
Hint:
- What type of figure (shape) forms the top of the prism? What type of figure forms the bottom of the prism?
- How can you find the area of these figures?
Volume
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Perseverance may be called for because the solutions to the problems may not seem immediately obvious. For example, some students, distracted by the different shapes of the four-sided, partial rectangular prisms, may not immediately realize that they must have the same surface areas, as they are formed from paper of the same area. It is not so easy or obvious without numerical calculation to determine which rectangular prism has the greater volume.
Interventions
Student has difficulty reasoning about the amount of space inside the two prisms.
- Just by looking, does one prism appear to have more room inside than the other prism?
- If you could fill the prisms with water, which prism do you think would hold more?
- It is okay if you can't tell at this point which prism has more space inside.
Possible Answers
- Predictions will vary.
Work Time
Volume
- Predict which prism has the greater volume (that is, which prism has more “space inside”). Explain your thinking.
Hint:
- If you put one prism in the other prism, how can that help you predict the volume?
- Do you know the height of the prism or the area of the base?
- How can you check your prediction?
Prepare a Presentation
Prepare for Ways of Thinking
Select examples of the following student work to share during Ways of Thinking:
- Correct and incorrect ways of reasoning about how the total surface area of the four sides of one prism compares to the total surface area of the four sides of the other prism
- Correct and incorrect ways of reasoning about how the total surface area of all six faces of one prism compares to the total surface area of all six faces of the other prism
- Interesting ways of reasoning about which prism has more space inside (i.e., the greater volume)
Challenge Problem
Answers
- The difference in surface areas of the half-sheet prisms would be greater. The surface areas of the top and bottom faces of the shorter half-sheet prism and the shorter whole-sheet prism would be the same, but the surface areas of the top and bottom faces of the taller half-sheet prism would be smaller than the surface areas of the top and bottom faces of the taller whole-sheet prism.
Work Time
Prepare a Presentation
- Explain what you learned about surface area and volume of rectangular prisms. Use your work to support your explanations.
Challenge Problem
Suppose that you made two other prisms, but this time you started with a half-sheet of paper like the one in the diagram. (The half-sheet measures 4 by 11 inches.) Assume that these prisms have tops and bottoms.
- Compare the surface area of the prisms made with half-sheets to those made with whole sheets.
- How does the total surface area of each of these prisms compare to the whole-sheet prisms?
- Which set of prisms (the half-sheets or whole-sheets) has a greater difference in total surface area between the two types (short and tall) of prisms? Explain.
Make Connections
Mathematics
Have students share the reasoning they used to compare the combined surface areas of the four faces of the two prisms. Then have them share how they compared the combined surface areas for all six faces of the two prisms.
Ask some students to share their predictions and reasoning about how the amount of space inside the prisms compare. Tell students they will check their predictions in Lesson 6.
Invite students who solved the Challenge Problem to share their answers and reasoning. Encourage these students to present their arguments as clearly and precisely as possible. Invite other students to ask questions and critique the reasoning of the presenters.
ELL: List all student responses, potential difficulties, and possible conclusions in these problems. As students are working through the problems, they can refer to the list of difficulties and discuss ways of resolving them. Encourage ELLs to use their prisms to aid them in their explanations.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ thinking concerning the surface areas and volumes of the different prisms.
Hint:
As your classmates present, ask questions such as:
- How did you determine the side lengths for each prism?
- How did you determine the total surface area?
- Explain your thinking about how adding a top and bottom to a prism affects its area.
- How is your explanation about how to predict the volume of a prism similar to the last explanation we heard? How is it different?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students wonder about rectangular prisms. If any reflections look interesting enough to pursue later, record them in a class notebook.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about rectangular prisms is …