- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Identifying Nets For Cubes

Overview
Lesson Overview
Students explore nets—2-D patterns that can be folded to form 3-D figures. They start by examining several patterns and determining which nets form a cube. Then, they sketch nets for rectangular prisms. They also find the surface area of the rectangular prisms.
ELL: Remind students of the units used to measure area and volume. Use this opportunity to reinforce why square units are used for area (2-D) and cubed units are used for volume (3-D).
Mathematics
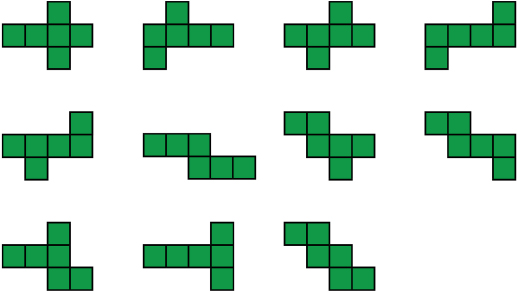
A net is a 2-D pattern that can be folded to form a 3-D figure. In this lesson, the focus is on nets for rectangular prisms. There are many possible nets for any given prism. For example, there are 11 different nets for a cube, as shown below.
The surface area of a prism is the area of its net.
Goals and Learning Objectives
- Identify nets for cubes.
- Sketch the net of a rectangular prism.
- Find the surface area of a rectangular prism.
Introduction to Nets
Lesson Guide
Have students watch the video and describe the process of turning a 3-D cube into a 2-D figure.
Tell students that a 2-D pattern that folds up to create a 3-D figure is called a net.
SWD: Go over the mathematical language used throughout the module. Make sure students use that language when discussing the problems.
- surface area
- net
- rectangular prisms
Opening
Introduction to Nets
Watch the video. Then, discuss the following concepts.
- The 2-D version of a cube is called a net.
- The surface area of a prism is the area of its net.
- You can find the surface area of a 3-D figure by adding together the areas of each surface.
- The surface area of a cube with side lengths of 1 unit is 6 square units.
VIDEO: Cube
Math Mission
Lesson Guide
Discuss the Math Mission. Explain that students will be creating nets for rectangular prisms to determine the surface areas of the prisms.
Opening
Create and analyze 2-D nets of 3-D figures to determine the surface areas of the figures.
Explore Nets
Lesson Guide
Tell students that they are going to look at different arrangements of squares and decide which arrangements are nets of cubes and which are not. Then they will sketch nets to determine the surface area of rectangular prisms.
Have students work solo to start and then move into partner work after a few minutes.
Students who are having trouble identifying the nets of cubes may wish to copy the nets onto grid paper, cut them out, and fold them.
SWD: Provide physical manipulatives to support students' understanding between the net and a prism. Provide graph paper with large squares and tape to assist students in physically building the prisms. Some students may need to build each cube from the given nets to make a conclusion.
Mathematical Practices
Mathematical Practices 5: Use appropriate tools strategically.
To identify which nets form cubes, some students may want to copy the patterns onto grid paper, cut them out, and fold them.
If cubes are available, some students may choose to use them to build the prisms. If they build each prism using a net drawn on a sheet of paper, they will be able to easily turn it to look at the faces.
Interventions
Student has difficulty identifying which patterns are nets for cubes.
- Try to visualize folding the pattern.
- Will any of the squares overlap?
- If the squares overlap, will the net form a cube? How do you know?
- Copy the pattern onto grid paper. Then cut it out and fold it.
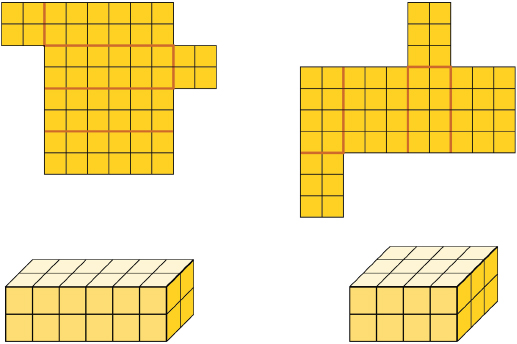
Answers
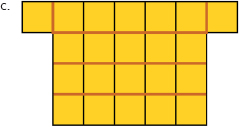
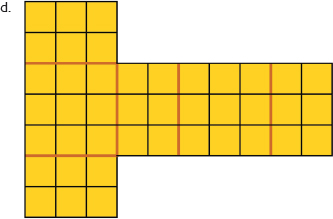
- They are all nets of cubes except for net d and net e.
- Explanations will vary.
Work Time
Explore Nets
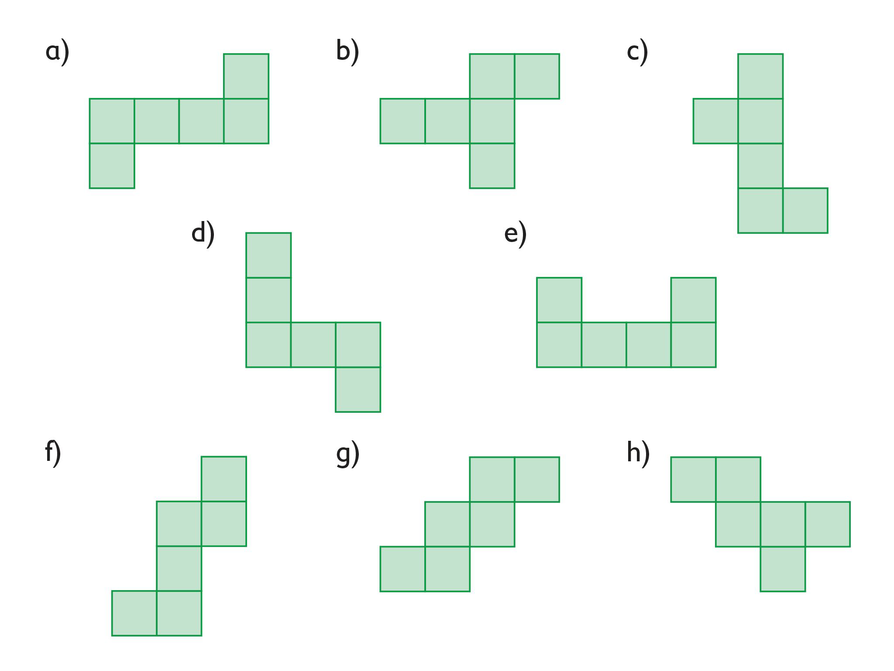
- Which of the nets in the diagram are nets of cubes?
- Explain your thinking.
Make Nets
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
After sketching the nets for the rectangular prisms, students may want to check their nets by cutting them out and folding them.
Interventions
Student has difficulty sketching the nets.
- Try sketching the bottom of the prism first.
- Now, start with one side of your bottom rectangle. What does the face of the prism that is attached to it look like? Sketch that next.
- When you have sketched all the sides, think about where the top should go. Is there more than one possibility?
- How can you check your net to make sure it works?
Student sketches an incorrect net.
- How many faces should your net have?
- How many pairs of identical faces should your net have?
- Did you try cutting out your net and folding it?
Possible Answers
Work Time
Make Nets
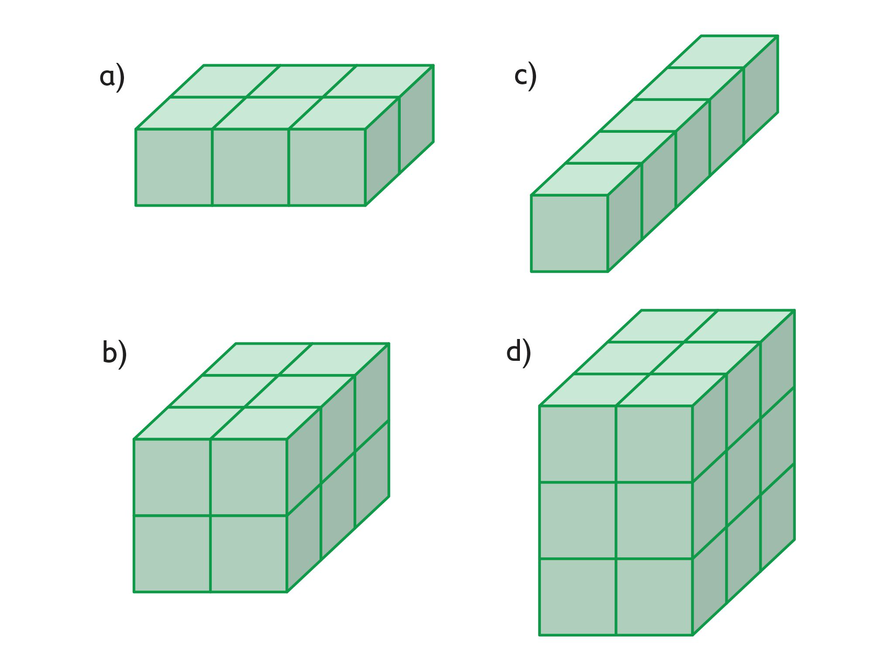
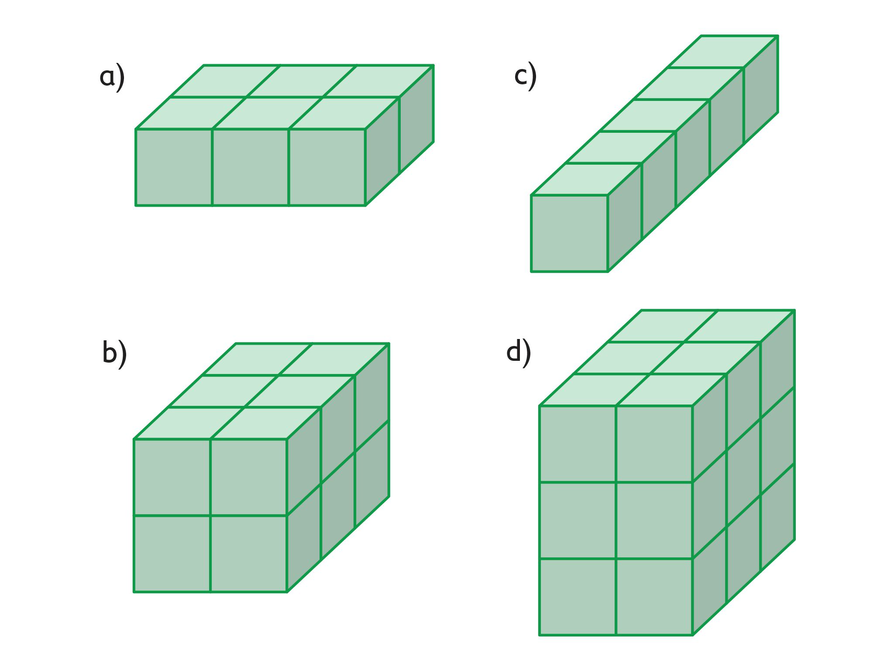
- Draw a net for each rectangular prism.
Hint:
There are many possible nets. Try sketching the bottom face of the prism in the center of a grid. Look at the prism and determine which surfaces share a common side with this bottom face. Then draw these surfaces, connecting them to the bottom face at the shared side. Where would you draw the top of the prism?
Explore Nets and Surface Area
Interventions
Student cannot find the surface area of a rectangular prism.
- How many square units are in the net? How does that relate to the surface area of a rectangular prism?
Answers
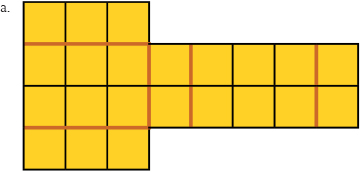
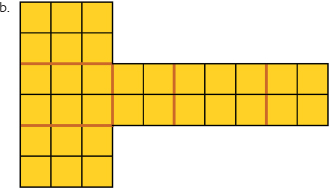
a. The surface area is 22 square units.
b. The surface area is 32 square units.
c. The surface area is 22 square units.
d. The surface area is 42 square units.
Work Time
Explore Nets and Surface Area
- Find the surface area of each rectangular prism. Use the nets you drew.
Prepare a Presentation
Preparing for Ways of Thinking
Listen for the different ways students are reasoning about which nets form cubes and which do not. Identify students with different ways of thinking to share in the discussion later.
As students sketch nets for the rectangular prisms, select two or three different nets for each prism to be presented during Ways of Thinking. Also, look for students who are reasoning about the nets in interesting (correct and incorrect) ways. Have these students explain their strategies during Ways of Thinking.
Challenge Problem
Answers
- Nets of a rectangular prism made up of 24 cubes will not always look the same. Examples will vary. Possible examples:
Work Time
Prepare a Presentation
- Show one of the prism nets you drew and explain why it represents the prism. (You might want to print your drawing, cut it out, and then assemble it to prove that your net represents the prism.)
- Explain how you determined the surface area of the prism.
Challenge Problem
- Several different rectangular prisms are each made up of 24 cubes. Will their nets all look the same? Provide examples to support your answer.
Make Connections
Lesson Guide
Ask students to share the strategies they used to decide whether a figure is a net for a cube.
Then have students give their presentations. Be sure to have students who used different nets for the same rectangular prism present. In the discussion, bring out the fact that although nets for the same rectangular prism can look different, the nets will always have the same number of square units, so the surface area will always be the same.
SWD: While all students should be working on speaking and listening skills, some students with disabilities may be reluctant to speak in front of peers.
Offer students alternate means of demonstrating an understanding of the skills and concepts. For example:
- Allow an alternate means of making the presentation such as a video or audio recording.
- Present to a partner or smaller group rather than the whole class.
- Assign different presentation-related roles to group members (materials management, note-taker, director, etc.) who are less comfortable.
- Provide additional opportunities to rehearse what will be presented. Have students create cue cards to refer to throughout the presentation in order to lessen anxiety and reliance on memory.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
During the discussion, if there is any disagreement about whether a figure is a net of a cube or a prism, put students in groups to check. Then have students share their work.
Performance Task
Ways of Thinking: Make Connections
- Take notes about your classmates’ explanations of their net drawings and how they calculated surface area.
Hint:
As your classmates present, ask questions such as:
- Explain your strategy for creating a net.
- Do you think it’s easier to determine the surface area from the net or from the three-dimensional figure?
- How could you check whether you found the correct surface area?
- How do you know that your net accurately represents the prism?
Surface Area and Nets of Rectangular Prisms
Lesson Guide
Have pairs quietly discuss how to use a net to determine the surface area of a rectangular prism.
As student pairs work together, listen for students who may still have misconceptions so you can address them in the class discussion.
Mathematics
After a few minutes, discuss the summary as a class. Review the following points:
- A 2-D pattern that can be folded to form a 3-D figure is a net for that 3-D figure.
- Any rectangular prism can have many different nets.
- One strategy for sketching a net is to sketch the bottom first and then to sketch the side that is attached to each edge.
- The surface area of a prism is the area of its net.
Formative Assessment
Summary of the Math: Surface Area and Nets of Rectangular Prisms
Read and Discuss
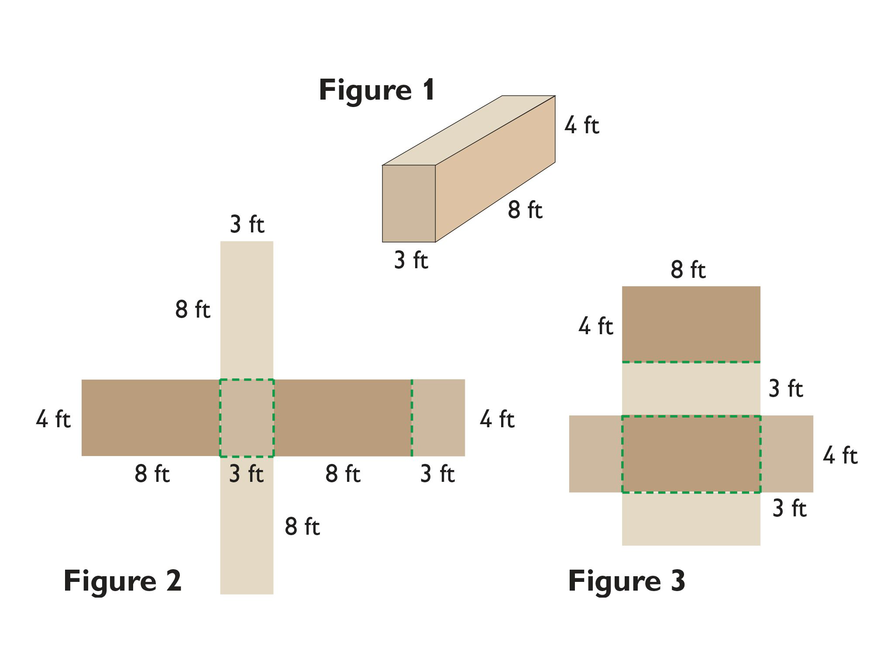
- A rectangular prism is a prism in which all faces are rectangles. There are many ways to “cut” along the edges of the prism in order to lay it flat (and thus make a net of the prism). Figures 2 and 3 show two different ways to make a net of the rectangular prism in Figure 1.
- The surface area is the total area of the six rectangles that form the six faces of the prism. Regardless of which net you use, you will find that the surface area is 176 ft2.
Hint:
Can you:
- Explain what a net is?
- Give at least one strategy for sketching the net of a rectangular prism?
- Define surface area?
- Describe how to use the net of a three-dimensional object to find its surface area?
- Explain why the surface area that you calculate from two different nets of the same three-dimensional object will be the same?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to learn how students can use the net of a 3-D figure to determine its surface area.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I can find the surface area of three-dimensional figures using nets by …