Using A Grid To Calculate The Area Of An Irregular Figure

Overview
Lesson Overview
Students estimate the area of Lake Chad by overlaying a grid on the map of the lake.
Key Concept
The area of an irregular figure can be found by overlaying a grid on the figure. By estimating the number of grid squares the figure covers and multiplying by the area of each square, you can find the approximate area of the figure. The accuracy of the estimate depends on the size of the grid squares. Using a smaller grid leads to a more accurate estimate because more whole grid squares are completely filled. However, using a smaller grid also requires more counting and more combining of partially-filled squares and is, therefore, more time-consuming. Using a larger grid gives a quicker, but rougher, estimate of the area.
Goals and Learning Objectives
- Use a grid to find the area of an irregular figure.
Materials
- Map of Lake Chad handout (one for each pair of students)
- Rulers, optional (one for each pair of students)
Lake Chad
Lesson Guide
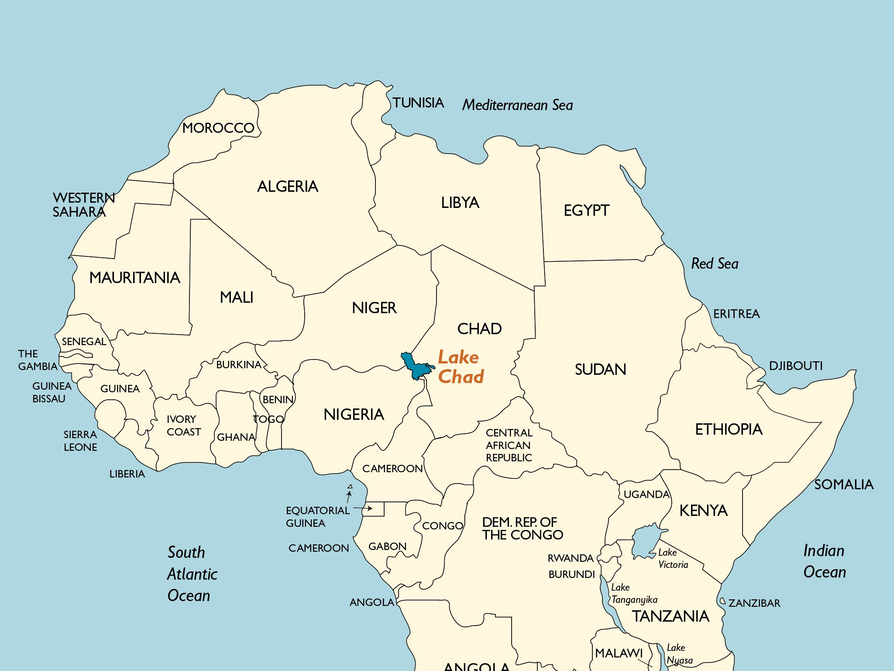
Have students look at the photo of Lake Chad from space and where Lake Chad is on the map of Africa. Have partners discuss how they would find the area of the surface of the lake.
SWD: Students with disabilities may not as readily connect new information to previously learned skills and concepts. Activate background knowledge about area to promote connections between this and the new topic being investigated here.
Opening
Lake Chad
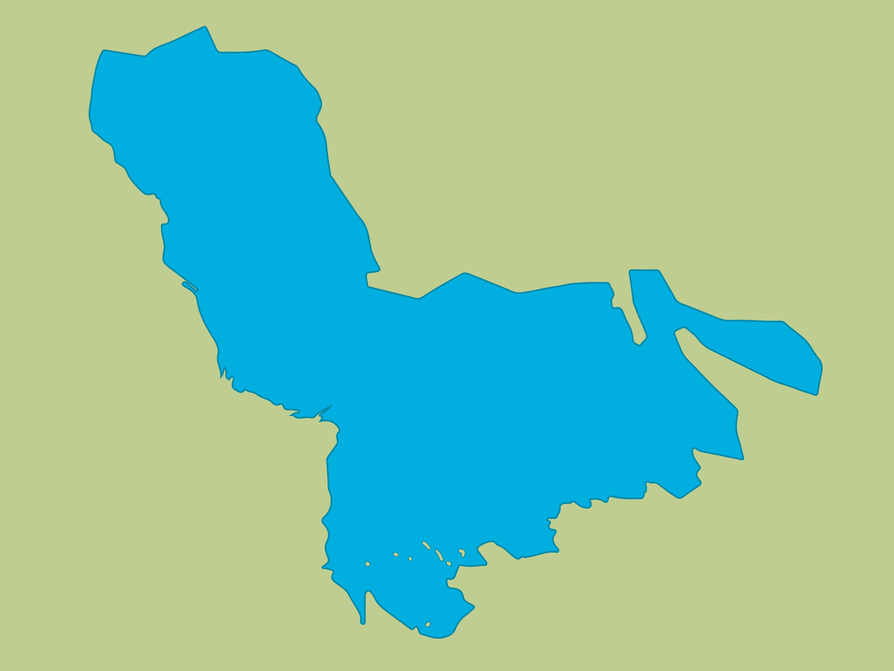
- Use the map to locate where Lake Chad is in Africa.
- This picture of Lake Chad in Africa was taken by the Apollo 7 astronauts from space in 1968. The area of Lake Chad has decreased significantly since this photograph was taken.
- Discuss why the changes in the area of Lake Chad might be interesting to scientists, and how they might determine the surface area of the lake.
An Irregular Figure
Lesson Guide
Have partners continue to discuss strategies for finding the area of the surface of the lake. Answers will vary, but should include at least one idea of how they will find the surface area. Estimation, measuring the dimensions, and trying to break it into smaller figures are all possibilities. Remind students of what they already know about finding area if needed.
ELL: Be aware that students will probably be unfamiliar with Lake Chad. It is important to provide relevant examples in order for students to understand and connect with the mathematics. Discuss why there would be a need to find the area of Lake Chad.
Opening
An Irregular Figure
This map shows the shape of Lake Chad when it is full. The shape of Lake Chad would be called an irregular figure.
- What strategy can you use to find the area of the surface of the lake?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will estimate the area of Lake Chad using a grid.
SWD: Using approximation and estimation can be challenging for some students. Review and reinforce this skill with students prior to having them start the tasks in which they will be expected to approximate or estimate.
Opening
Estimate the area of an irregular figure using a grid.
Estimate the Surface Area of Lake Chad
Lesson Guide
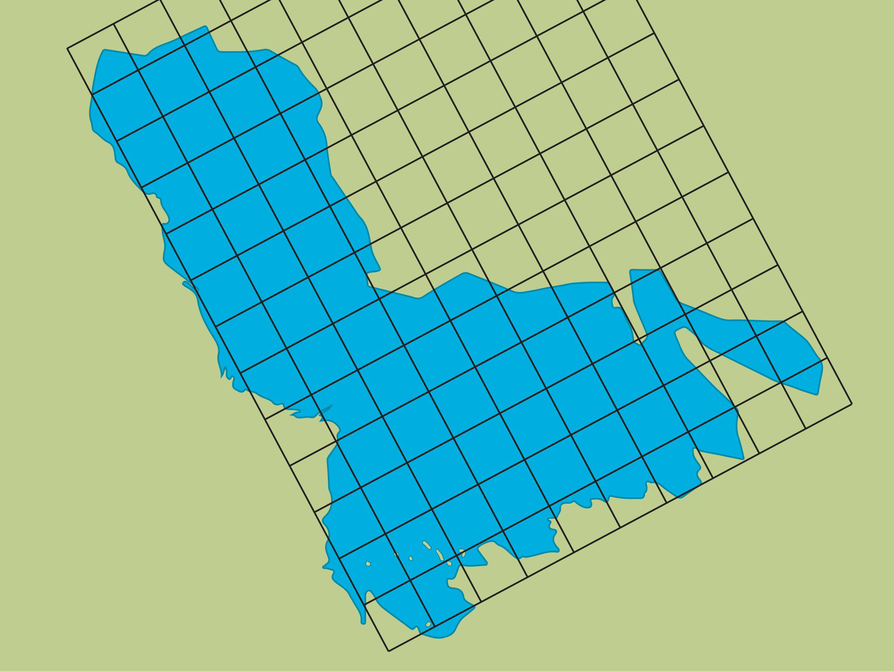
Have students look at the map with the grid. Explain that each grid square represents a 10 by 10 mile square. Have students work solo to start. After a few minutes, have students work with a partner to complete the problem and to prepare the presentation.
Use the following questions to help students who have trouble getting started:
- What area does one square on this grid represent? (Answer: 100 mi2)
- What are the approximate dimensions of the lake?
[common error] Students may think the area of a grid square is 10 mi2, rather than 100 mi2. Point out that the side length of each square is 10 mi. Ask students to find the area of a square.
Students who complete the Challenge Problem will need rulers and extra copies of the map.
ELL: Developing and deepening student understanding of terms is essential. Building vocabulary and concepts in the context of real-world problems and experiences ensures that students will “own” the new words and concepts they encounter.
SWD: Circulate during Work Time and help students to identify ideas from their notes or work that are appropriate to contribute during the upcoming Ways of Thinking discussion.
Mathematical Practices
Mathematical Practice 7: Look for and make use of structure.
Identify students who are making use of structure. For example, a student may sketch rectangles or triangles that approximate part of the lake's shape and find the areas of these figures using formulas, rather than by counting individual grid squares.
Interventions
Student has difficulty getting started.
- Find a grid square that is completely blue. What is the area of the part of the lake in that square?
- How can you find the total number of grid squares that are completely blue?
- How should you count the grid squares that are partially blue?
Student works unsystematically.
- How can you mark the squares to keep track of the ones you have counted?
- If you combine partially blue squares to get one completely blue square, how can you indicate this on the grid?
After counting the grid squares, student does not know how to find the area.
- What are the dimensions of each grid square?
- What is the area of each grid square?
- If you know the number of grid squares the lake covers and the area of each square, how can you find the total surface area of the lake?
Possible Answers
- Slanting the grid covers more of the lake with whole grid squares.
- Estimates will vary.
Possible answer: By counting and combining squares, I estimate that the lake fills about 65 grid squares. Each grid square is 10 mi by 10 mi, so its area is 100 mi2. The area of the surface of the lake is about 65 ⋅ 100 = 6,500, or 6,500 mi2.
Work Time
Estimate the Surface Area of Lake Chad
One method geographers use to find the area of an irregularly shaped lake is to use a grid.
The scale of the grid shown on this image of Lake Chad is each small square represents a 10 mile by 10 mile area.
- Why do you think the grid is slanted?
- Make an estimate of the area of the lake using the grid.
Hint:
- What is the area of one square?
- If a square completely overlaps the lake, what do you know?
- If a square only partially overlaps the lake, what can you do?
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who are using different strategies to estimate the area of the lake to present in Ways of Thinking.
Have students who solve the Challenge Problem share their different-sized grids in Ways of Thinking.
ELL: Allow ELLs to write up parts of their answers. It can be hard for ELLs to explain the whole phrase, but they can either draw what they mean or show a diagram or a picture. This applies to all of the answers.
Challenge Problem
Possible Answers
- Using a smaller grid covers more of the lake with whole squares, which will give a more accurate estimate of the area of the surface of the lake. However, a smaller grid also requires more counting and combining to find the total surface area. A larger grid allows for a quicker, but rougher, estimate of the area of the surface of the lake.
Work Time
Prepare a Presentation
- Explain how you found the area of Lake Chad.
- Support your explanation mathematically.
Challenge Problem
Suppose the grid were a different size—either smaller or larger.
- What would be the advantages and disadvantages of using a smaller versus a larger grid size?
Make Connections
Lesson Guide
Discuss the slanted grid and have students talk about how the slant of the grid makes it easier to calculate the area.
Have students share their different solutions for finding the surface area of Lake Chad.
For the Challenge Problem, talk about the advantages and disadvantages of different grid sizes. Elicit that a larger grid size makes it easier to count squares, but a smaller grid size gives a more accurate estimate.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Have students show their strategies for estimating the surface area of the lake. Students should describe how they kept track of the squares they counted and how they counted partially blue squares. Students who found shortcuts to avoid having to count each individual square should share their methods.
Mathematical Practice 6: Attend to precision.
Have students who worked on the Challenge Problem share their work. Encourage students to communicate their reasoning as precisely as possible.
Performance Task
Ways of Thinking: Make Connections
- Take notes about other classmates’ methods for finding the area of Lake Chad.
- How close is your estimate to that of the rest of the class?
- If your estimate is larger or smaller, can you explain why? What did you do differently?
Hint:
As your classmates present, ask questions such as:
- How did you calculate the area?
- What strategy did you use to calculate the area in a square that did not completely cover the lake?
- Why would you use this method to determine the area, as opposed to dividing the figure into composite figures as in the last lesson?
- Why do you think the problem used the term surface area rather than justarea ?
Compare Methods of Finding Area
A Possible Summary
If the figure is irregular, you can put a grid on top of it and use the grid to estimate the area of the figure. The larger the squares on the grid, the easier the squares are to count. The smaller the squares on the grid, the more accurate the area measurement will be.
An advantage of the grid method is that it is good for finding the area of irregular figures. A disadvantage of this method is that it is just an estimate and it is time-consuming to use.
If the figure is not irregular, you can decompose the figure into basic figures and then find the sum of their areas to find the total area of the original figure.
An advantage of the decomposition method is that you can use formulas to find the areas. A disadvantage of this method is that it is accurate for only composite figures, not irregular figures.
Formative Assessment
Summary of the Math: Compare Methods of Finding Area
- Write a summary that describes and compares the method for finding area using a grid versus the method for finding area by decomposing a figure into smaller figures.
- Discuss when you would use each method and the advantages and disadvantages of each method.
Hint:
Check your summary.
- Do you explain how to use the grid method to find area?
- Do you explain how to use the decomposition method to find area?
- Do you discuss when to use each method?
- Do you discuss the advantages and disadvantages of each method?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students learned about finding areas.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something new I learned today about finding areas is …