Transforming The Net of A Cube Into The Net of A Pyramid

Overview
Lesson Overview
Students use scissors to transform a net for a unit cube into a net for a square pyramid. They then investigate how changing a figure from a cube to a square pyramid affects the number of faces, edges, and vertices and how it changes the surface area and volume.
Key Concepts
A square pyramid is a 3-D figure with a square base and four triangular faces.
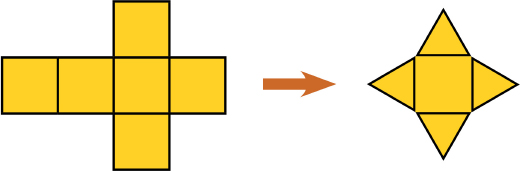
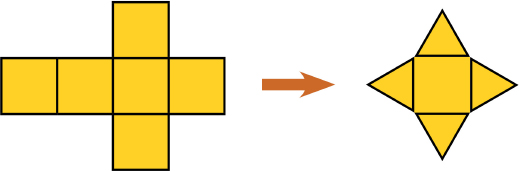
In this lesson, the net for a cube is transformed into a net for a square pyramid. This requires cutting off one square completely and changing four others into isosceles triangles.
It is easy to see that the surface area of the pyramid is less than the surface area of the cube, because part of the cube's surface is cut off to create the pyramid. Specifically, the surface area of the pyramid is 3 square units, and the surface area of the cube is 6 square units. Students will be able to see visually that the volume of the pyramid is less than that of the cube.
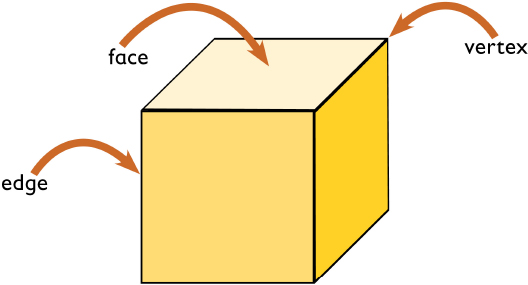
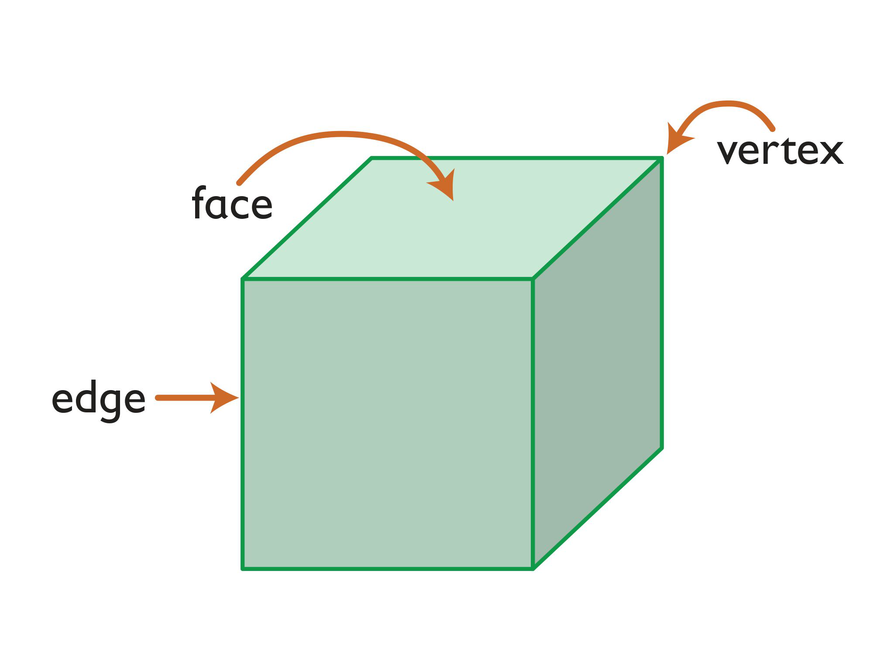
Students consider the number of faces, vertices, and edges of the two figures. A face is a flat side of a figure. An edge is a segment where 2 faces meet. A vertex is the point where three or more faces meet. A cube has 6 faces, 8 vertices, and 12 edges. A square pyramid has 5 faces, 5 vertices, and 8 edges.
Goals and Learning Objectives
- Change the net of a cube into the net of a pyramid.
- Find the surface area of the pyramid.
Introduction to Nets of Pyramids
Lesson Guide
Have students look at the images of the pyramid and the net for the cube. Explain that the pyramid was made by cutting away parts of the cube net and then folding it. Have students discuss with their partners about how they could change the net for the cube into a net for the pyramid.
ELL: Explain new terms to students before the terms are used in problems. Remember, ELLs are learning new concepts (math) and a new language at the same time. Discuss and define the following terms:
- square pyramid
- isosceles triangle
- edge
- face
- vertex
Opening
Introduction to Nets of Pyramids
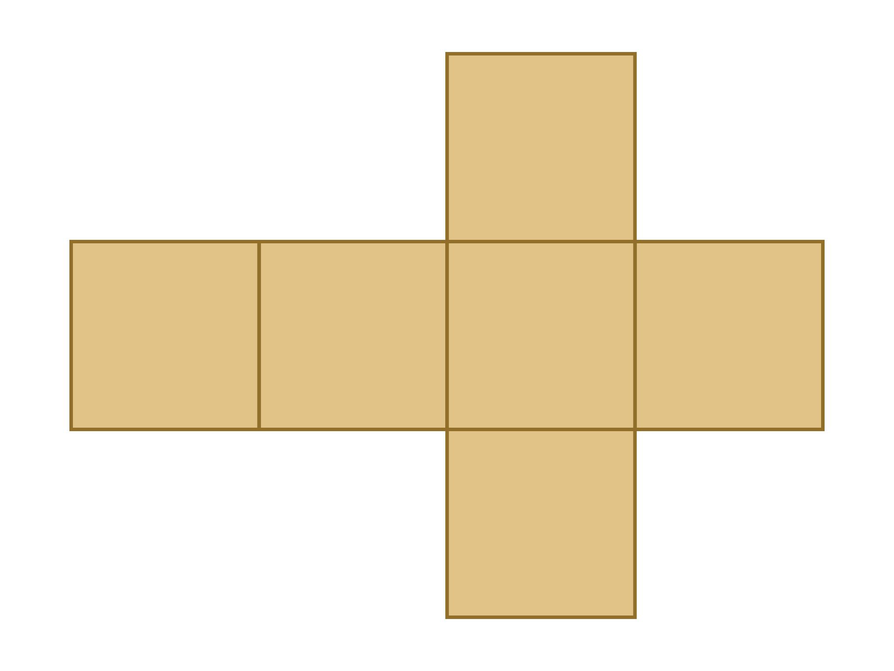
The pyramid shown in the first image was made using the net of a cube (shown in the second image). Before the net was folded to form the pyramid, some paper was cut off. No paper was added.
- How could the net of the cube have been cut to turn it into a net of the pyramid?
This pyramid was made…
...by modififying this net using scissors.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will investigate how changing a figure from a cube to a square pyramid affects the number of faces, edges, and vertices and how it changes the surface area and volume.
Opening
Investigate the surface area and volume of a pyramid.
Build a Pyramid
Lesson Guide
Provide students with inch grid paper and scissors to make their nets. Have students work solo when creating their net of a pyramid and then move into partner work.
SWD: Prior to the Ways of Thinking discussion, circulate and check in with students. Preview the questions that will be discussed with students who may need additional time to process the information.
Also, provide students with several of the key questions in written form (digitally). This will allow students who become anxious when put on the spot to prepare answers for questions that they can successfully share in the class discussion.
Interventions
Student has difficulty transforming the net for a cube into a net for a pyramid.
- What figure is the base of the cube? What figure is the base of the pyramid?
- Besides the base, how many faces does the pyramid have? How does this compare to the cube?
- What types of triangles make up the faces of the pyramid?
- How can you cut a square face to form an isosceles triangle?
Answers
Work Time
Build a Pyramid
Start with the net of a cube.
- Use scissors to transform it into the net of a pyramid.
Faces, Vertices, and Edges
Lesson Guide
Point out the vocabulary and make sure students understand the words edge, vertex, and face.
Ask students who are having trouble:
- What changed as the figure went from being a cube to a pyramid?
- Are the bases of the cube and the pyramid the same or different?
Answers
- There are 6 faces, 8 vertices, and 12 edges in the original cube, and there are 5 faces, 5 vertices, and 8 edges in the pyramid.
Work Time
Faces, Vertices, and Edges
- Compare the numbers of faces, vertices, and edges of a cube with the numbers of faces, vertices, and edges of the pyramid you made.
Hint:
- A face is a flat side of a solid figure.
- An edge is a line segment where two faces meet.
- A vertex (plural vertices) is a point where three or more faces meet.
Surface Area
Lesson Guide
Remind students that they learned to calculate the surface area of the cube in the previous lesson.
Ask students who are having trouble:
- Which looks like it has more space inside—the cube or the pyramid? Why do you think that?
- What did you do to the net of the cube to get the net of the pyramid? How does that affect the surface area of the pyramid compared with the surface area of the cube?
Interventions
Student has difficulty comparing the surface area and volume of the cube to the surface area and volume of the pyramid.
- How does the area of the net relate to the surface area of the 3-D figure it folds into?
- When you made the pyramid, you cut away part of the cube net. What does this tell you about how the surface areas of the cube and pyramid compare?
- How does the space inside the pyramid compare to the space inside the cube?
Student has difficulty finding the surface area of the pyramid.
- What figures form the net for the pyramid?
- How do you find the area of the square?
- How do you find the area of each triangle?
- The area of the square is 1 square unit.
- How much of each square did you cut away?
- What is the area of the triangle that is left?
Answers
- As the figure changes from a cube to a pyramid, both the surface area and volume decrease.
- The surface area of the cube is 6 square units. The surface area of the pyramid is 3 square units.
Work Time
Surface Area
- How do you think your paper cutting will affect the surface area and volume of the resulting figure (the pyramid) as compared to the original figure (the cube)?
- Find the surface area of the cube and the pyramid. (Each edge of the cube has a length of 1 unit.)
Prepare a Presentation
Preparing for Ways of Thinking
Look for examples of both correct and incorrect nets, and listen for different ways that students are reasoning about making the nets. Look for students who are finding the surface area of the prism by using area formulas and those who are using reasoning. (For example, the area of the square base is 1 square unit. You cut away half of a square face to make a triangular face, so the area of each triangular face is square unit.) Highlight these solutions in Ways of Thinking.
Challenge Problem
Answers
- The height of each triangle forming the pyramid is the same as the height of each side of the cube, but the pyramid is shorter than the cube because the four triangles are tilted inward to meet at the top vertex.
Work Time
Prepare a Presentation
- Explain your strategy for comparing the volume of a pyramid to the volume of the cube. Support your explanation with the pyramid you made.
- Explain your strategy for determining the surface area of a pyramid. Support your explanation with the pyramid you made.
Challenge Problem
- Is the pyramid taller or shorter than the cube? Explain.
Make Connections
Mathematics
Have students share the counts they got for the faces, edges, and vertices of the cube and the pyramid.
Have students give their presentations. Discuss how the paper cutting affected the surface area and volume as the cube was transformed into a square pyramid. Elicit that since parts of the net were cut off to make the pyramid, the surface area of the pyramid must be less than the surface area of the cube.
Students should also recognize that the pyramid will have less volume than the cube. Have them explain why.
Discuss different methods students used to find the surface areas of the cube and the square pyramid.
Have the students who did the Challenge Problem explain their thinking.
SWD: Provide these students with a template to organize the information in their presentations. This will help you to ensure that they include all the required information. The template should include space for recording all information for comparing cubes and square pyramids. Provide space for students to record observations about faces, edges, vertices, surface area, and volume.
ELL: Be cognizant that ELLs may encounter difficulties when they have to express themselves using the English language. If you hear them say the right things but using the wrong grammar structure, show signs of agreement and softly rephrase using the correct grammar. Use the student's words as much as possible.
Mathematical Practices
Mathematical Practice 7: Look for and make use of structure.
Ask students to discuss how they looked for and made use of structure to transform the net of the cube into a net of a square pyramid. For example, students may have noticed that the pyramid had one fewer face than the cube and reasoned that they would have to cut off one square from the net. They may have looked at the fact that each side of a square base of the pyramid is connected to an isosceles triangle face to determine how the figures in their net should be organized.
Performance Task
Ways of Thinking: Make Connections
- Take notes about your classmates’ strategies for comparing the volume and surface area of a pyramid to the cube it was made from.
Hint:
As your classmates present, ask questions such as:
- What strategy did you use to compare the volume of the cube to the volume of the pyramid?
- How did you find the surface area of the cube?
- How did you find the surface area of the pyramid?
More About Pyramids
A Possible Summary
You can cut the net of a cube to make a net for a square pyramid.
There are 6 faces, 8 vertices, and 12 edges in a cube, and there are 5 faces, 5 vertices, and 8 edges in a square pyramid.
The volume and surface area of the square pyramid will be less than the volume and surface area of the cube, because you cut away area to make the net of the square pyramid.
To find the surface area of the cube, you can find the surface area of one face and then multiply by 6:
1 unit × 1 unit = 1 square unit
1 square unit × 6 = 6 square units
To find the surface area of the square pyramid, you can find the surface area of the square face and then add the surface areas of the 4 triangular faces:
1 unit × 1 unit = 1 square unit
(1 unit × 1 unit) = square unit
square unit × 4 square units = 2 square units
1 square unit + 2 square units = 3 square units
Formative Assessment
Summary of the Math: More About Pyramids
- Write a summary about what you discovered about the volume and surface area of a prism and a pyramid.
Hint:
Check your summary:
- Do you explain how you compared the volume of the pyramid to the volume of the cube it was made from?
- Do you explain how you found the surface area of the cube?
- Do you explain how you found the surface area of the pyramid?
Packing a Truck
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also, note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
Interventions
Student has difficulty getting started.
- What do you know?
- What do you need to find out?
- What is one packing plan that you can try?
- Can you sketch a picture of a packing plan?
Student has not found a way to test different packing plans systematically.
- Can you find a way to organize the different packing plans you would like to try?
- Can you organize your work in a table?
Student has not found the best packing plan.
- Is there another packing plan you can propose?
Student produces a correct solution but does not give an explanation of why it is correct.
- Why is your method the best plan for packing the product for shipping?
Student presents work poorly.
- Would someone unfamiliar with your type of solution easily understand your work?
- Have you given enough explanation in your work and is it clear?
Student makes a calculation error.
- Check to see if you have made any errors in your calculations.
Student produces a correct solution and an explanation of why it is correct.
- If the company allowed it, could you fit any boxes into the empty space in the truck? If so, how many? Explain.
- Could you use a different method for finding the solution? If so, what would it be? Which method do you prefer? Why?
ELL: Provide ELLs and other students a sample or model for the concepts, strategies, and applications that will be addressed in the quiz, and the format you want them to follow. Be prepared to address and explicitly reteach or review vocabulary, concepts, strategies, and applications.
Possible Answers
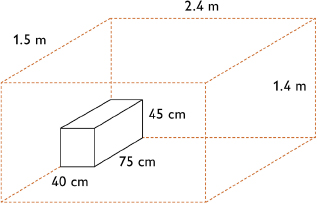
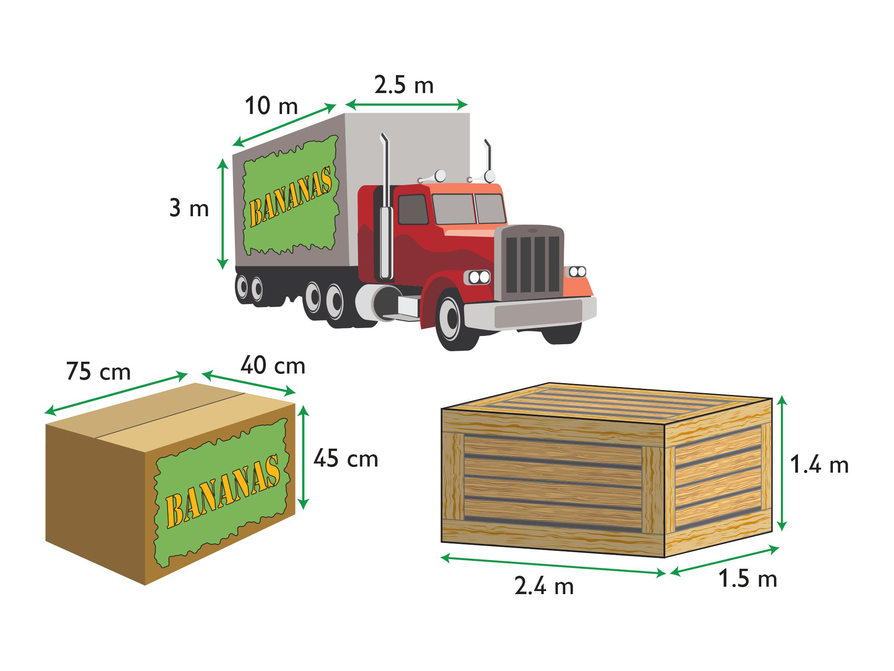
- Pack the boxes in the crate so that the 75 cm sides of the boxes are parallel to the 1.5 m side of the crate, and the 40 cm sides of the boxes are parallel to the 2.4 m side of the crate. This makes a 2 box by 6 box by 3 box prism, for a total of 2 ⋅ 6 ⋅ 3, or 36 boxes. The boxes will fit perfectly along the 2.4 m and 1.5 m sides of the crate, and there will be only a 5 cm gap along the other side.
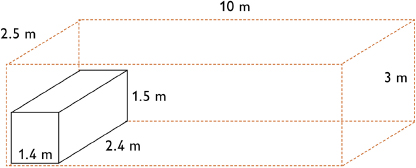
- Pack the crates in the truck so that the 1.5 m sides are parallel to the 3 m side of the truck, and the 2.4 m sides of the crates are parallel to the 2.5 m side of the truck. This makes a 2 crate by 1 crate by 7 crate prism, for a total of 2 ⋅ 1 ⋅ 7, or 14 crates. In all, there will be 14 ⋅ 36, or 504 boxes of bananas in the truck.
- The crates inside the truck form a 2.4 m by 3 m by 9.8 m prism, which has a volume of 70.56 m3. The truck bed is a 2.5 m by 3 m by 10 m prism, which has a volume of 75 m3. Only 4.44 m3 of the truck will be empty.
- Explanations will vary. Possible answer: This is the best plan because it minimizes the amount of unused space. Other ways of packing the crates (as listed below) will leave bigger gaps, and you will not be able to ship the maximum amount of product in each crate or truck:
- Put the 2.4 m sides of the crates parallel to the 2.5 m side of the truck and the 1.5 m sides of the crates parallel to the 10 m side of the truck. This would fit a 2 crate by 1 crate by 6 crate prism, for a total of only 12 crates.
- Put the 1.4 m sides of the crates parallel to the 2.5 m side of the truck. Only 1 crate would fit in this direction, leaving a 1.1 m by 10 m by 3 m gap, which is 33 m3.
- Put the 1.5 m sides of the crates parallel to the 2.5 m side of the truck. Only 1 crate will fit in this direction, leaving a 1 m by 10 m by 3 m gap, which is 30 m3, plus a 0.2 m by 1.5 m by 10 m gap on the top, which is 3 m3, for a total of 33 m3.
Formative Assessment
Packing a Truck
Complete this Self Check by yourself.
You are working for a trucking company that transports bananas. You are trying to transport the greatest number of bananas in each truckload. The bananas fill boxes, which are packed into crates. The crates are then packed into a truck.
- How can you pack each crate in order to fit the greatest number of boxes of bananas?
- How can you pack the truck in order to fit the greatest number of crates?
- Based on your packing plan, how much space in the truck will not be filled?
- Why is your packing plan the best possible plan?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students know about the difference between surface area and volume.
ELL: To assess their understanding of surface area and volume, ask students to write the definitions of the two terms in their own words. Assess both mathematical understanding and language. Make sure students compare the two definitions to explain their differences. Provide students with wait time and allow students access to their notes as a writing support.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some of the differences between surface area and volume are …