- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Cube Builder
Cube Builder
Volume Formula For Rectangular Prisms

Overview
Lesson Overview
Students build prisms with fractional side lengths by using unit-fraction cubes (i.e., cubes with side lengths that are unit fractions, such as unit or unit). Students verify that the volume formula for rectangular prisms, V = lwh or V = bh, applies to prisms with side lengths that are not whole numbers.
Key Concepts
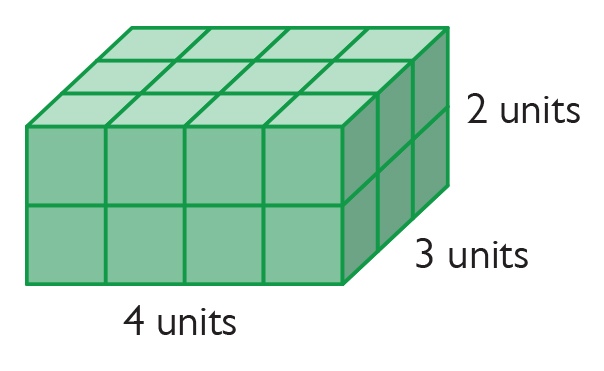
In fifth grade, students found volumes of prisms with whole-number dimensions by finding the number of unit cubes that fit inside the prisms. They found that the total number of unit cubes required is the number of unit cubes in one layer (which is the same as the area of the base) times the number of layers (which is the same as the height). This idea was generalized as V = lwh, where l, w, and h are the length, width, and height of the prism, or as V = Bh, where B is the area of the base of the prism and h is the height.
Unit cubes in each layer = 3 × 4
Number of layers = 5
Total number of unit cubes = 3 × 4 × 5 = 60
Volume = 60 cubic units
In this lesson, students extend this idea to prisms with fractional side lengths. They build prisms using unit-fraction cubes. The volume is the number of unit-fraction cubes in the prism times the volume of each unit-fraction cube. Students show that this result is the same as the volume found by using the formula.
For example, you can build a -unit by -unit by -unit prism using -unit cubes. This requires 4 × 3 × 2, or 24, -unit cubes. Each -unit cube has a volume of cubic unit, so the total volume is cubic units. This is the same volume obtained by using the formula V = lwh:.
-unit cubes in each layer = 3 × 4
Number of layers = 2
Total number of -unit cubes = 3 × 4 × 2 = 24
Volume = 24 × = cubic units
Goals and Learning Objectives
- Verify that the volume formula for rectangular prisms, V = lwh or V = Bh, applies to prisms with side lengths that are not whole numbers.
Volume of Cubes
Lesson Guide
Have students work in pairs to answer the questions, and then ask volunteers to share their answers and their reasoning.
Mathematics
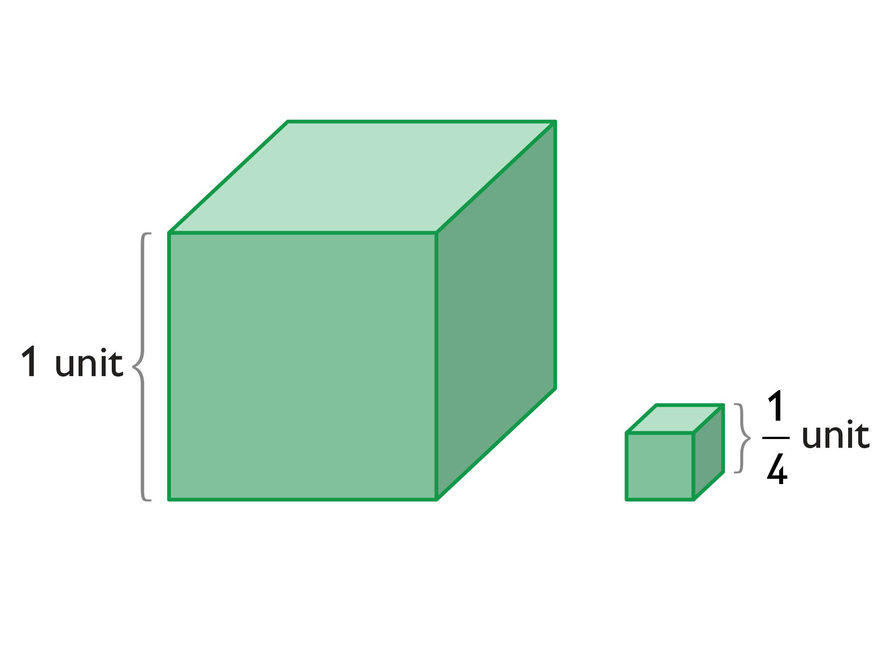
Sixty-four smaller cubes fit inside the unit cube. To see this, students can visualize four 4-by-4 layers of small cubes fitting inside the unit cube. This is a total of 4 · 4 · 4, or 64 cubes.
Because the unit cube has a volume of 1 cubic unit, each -unit cube has a volume of cubic unit.
[common error] Students may think that 4 of the small cubes fit inside the unit cube because the small cube is a -unit cube. Explain that the unit refers to the edge length of the cube, not its volume.
Opening
Volume of Cubes
The cube at the left of the diagram has edge lengths of 1 unit. The cube at the right has edge lengths of unit.
Volume is the amount of space inside a 3-D figure.
- How many -unit cubes fit inside the 1-unit cube?
- What is the volume of the -unit cube?
Math Mission
Lesson Guide
Discuss the Math Mission. Explain to students that they will be investigating whether the volume formula V = lwh works even if the dimensions of the prism are not whole numbers.
Opening
Build rectangular prisms with fractional edge lengths and find the volume of the prisms.
Find the Volume of Prisms
Lesson Guide
Introduce the Cube Builder interactive to students and make sure they know how to use it to make prisms with the unit-fraction cubes. Give students time to explore the Cube Builder interactive before they begin the problems.
Have students start the problems solo and then move into partner work after a few minutes.
For the first two problems, be sure students understand that they should first find the volume by reasoning (i.e., they should find the number of unit-fraction cubes in the prism and the volume of each unit-fraction cube). Then, they should apply the volume formula to see if they get the same result.
If students struggle to figure out how many -unit cubes to use in the first problem, suggest that they write all the dimensions as fractions with a denominator of 4. The dimensions are unit by unit by unit, so the prism should be 3 cubes by 5 cubes by 2 cubes.
[common error] Some students may get the wrong answers when they use the formula because they do not remember how to multiply with fractions and mixed numbers. Remind students to write all the factors in fraction form and then simply multiply numerators and then multiply denominators.
ELL: When listening to students' responses, give students advance notice they will be presenting their work on a specific problem during the Ways of Thinking section. This will give them ample time to prepare a thoughtful response.
SWD: Struggling students may still need explicit instruction for multiplying fractions. Provide small group instruction to make sure all students can multiply fractions accurately to find the volume of a rectangular prism.
Interventions
Student has difficulty building the 1-unit by -unit by -unit prism.
- Each cube has an edge length of unit. So, to know how many cubes to use, you need to figure out how many -units are in each dimension.
- Try writing the mixed numbers as fractions.
- How many fourths are in ? How many fourths are in ? How many fourths are in ?
Answers
- There are 30 -unit cubes in the prism.
- V = 30 · =
The volume of the prism is cubic unit, or cubic unit.
The volume is (or ) cubic unit, which is the same. Yes, the volume formula works for this prism.
Work Time
Find the Volume of Prisms
When a rectangular prism has whole-number edge dimensions, you can find its volume using the formula V = l ⋅ w ⋅ h, where l, w, and h represent the length, width, and height of the prism. Investigate whether this formula works even if the dimensions are not whole numbers.
Use the -unit cubes to build a prism with a length of 1 units, a width of units, and a height of unit.
- How many -unit cubes fit inside the prism?
- What is the volume of the prism?
- Does the volume formula
V = l ⋅ w ⋅ h (or V = lwh) work for this prism?
INTERACTIVE: Cube Builder
Hint:
How many 14 -unit cubes fit inside a 1-unit cube?
The Formula
Lesson Guide
In this problem, students must recognize that the volume of a -unit cube is cubic unit. Remind them of how they found the volume of a -unit cube in the Opening and suggest that they use similar reasoning for the -unit cube.
Interventions
Student gives the wrong volume for the prism made of -unit cubes.
- Try using the Cube Builder interactive to build a unit cube from the -unit cubes.
- How many cubes do you need?
- If the unit cube has a volume of 1 cubic unit, what is the volume of each of the -unit cubes?
Answers
- There are 40, -unit cubes in the prism.
The volume of each -unit cube is cubic unit.
The volume of the prism is cubic units.
The volume is cubic units, which is the same. Yes, the volume formula works for this prism.
Work Time
The Formula
Use the -unit cubes to build a prism with a length of 1 units, a width of 1 units, and a height of unit.
- How many -unit cubes fit inside the prism?
- What is the volume of each -unit cube?
- What is the volume of the prism?
- Does the volume formula V = lwh work for this prism?
INTERACTIVE: Cube Builder
Hint:
How many -unit cubes fit inside a 1-unit cube?
Applying the Formula
Lesson Guide
[common error] Some students may get the wrong answers when they use the formula because they do not remember how to multiply with fractions and mixed numbers. Remind students to write all the factors in fraction form and then simply multiply numerators and then multiply denominators.
SWD:
Struggling students may still need explicit instruction for multiplying fractions. Provide small group instruction to make sure all students can multiply fractions accurately to find the volume of a rectangular prism.
Answers
The volume is cubic unit.
Work Time
Applying the Formula
- Use the volume formula to find the volume of a prism with a length of unit, a width of unit, and a height of unit.
Using the Formula
Lesson Guide
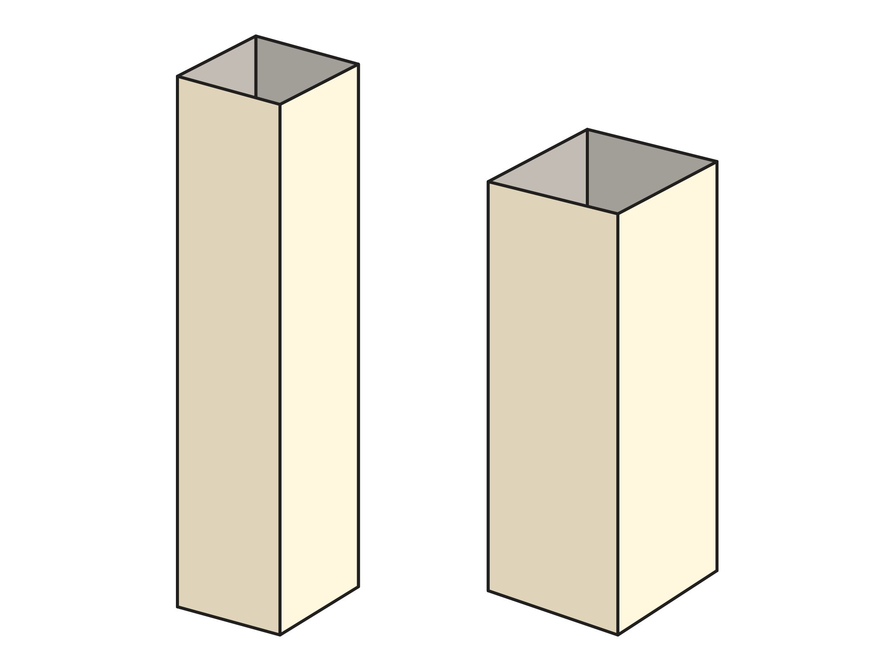
Remind students to look at the dimensions of the paper prisms they made in the previous lesson—they will need those dimensions for this problem.
[common error] Some students may get the wrong answers when they use the formula because they do not remember how to multiply with fractions and mixed numbers. Remind students to write all the factors in fraction form and then simply multiply numerators and then multiply denominators.
Interventions
Student can't calculate the dimensions of the prisms.
- Remember the dimensions of the paper you used to make the prisms, use those dimensions to help you find the dimensions of the prisms.
- When you fold the paper to make the prism, each side of the prism is one forth of the paper.
Answers
- Shorter prism:
The volume of the shorter prism is .
Taller prism:
The volume of the taller prism is . - Answers will vary. The shorter prism has the greater volume.
Work Time
Using the Formula
- Calculate the volume of each of the two prisms you made in Lesson 1.
- Was your prediction about which prism has the greater volume correct?
Hint:
Use the formula to find the volume of the prisms.
Prepare a Presentation
Prepare For Ways of Thinking
Look for students who are reasoning correctly and incorrectly about building the prisms and computing the volumes. Select these students to share their work during Ways of Thinking.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
In the Challenge Problem, students need to determine how to use only what they see in the video to estimate the volume of the cube and then to compare the volume of the cube with the volume of the man's body. Look for students who approach this problem in interesting or unique ways. These students can share their methods in Ways of Thinking.
Interventions
Student has trouble starting the Challenge Problem.
- To find the volume of a cube, what information do you need to know?
- How can you estimate the length of each edge of the cube?
- How does the man's height compare to the edge length of the cube?
- What would you estimate is the average height of a man?
Challenge Problem
Answers
- Answers will vary. Possible answer: I estimate the man is about 5 ft 8 in. tall. By comparing the edge length of the cube to the man's height, the edge length appears to be about 5 ft, so the volume is 5 · 5 · 5 = 125, or about 125 ft3.
- Answers will vary. Possible answer: If I estimate that the man is a rectangular prism with dimensions 5 ft high by 1 ft wide by ft thick, then his volume is , or about 5 ft3. Therefore, his body would take up , or about 5% of the cube.
Work Time
Prepare a Presentation
- Explain how you found the volume of one of the cubes from the lesson.
- Explain how you found the volume of one of the rectangular prisms from the lesson.
- Support your explanations with diagrams.
Challenge Problem
This video shows an act in which a man does acrobatics inside of a cube.
- Estimate the volume of the cube.
- Estimate the percentage of the volume of the cube that is taken up by the man’s body.
VIDEO: Aerial Cube Act
Make Connections
Lesson Guide
Have students share their presentations. Work together as a class to correct any errors and misconceptions.
Have students who did the Challenge Problem share their work.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
Ask students to explain, step by step, how they found their solutions. Encourage students to use clear, precise language.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Other students should critique the presenters' reasoning and make suggestions for how the solutions might be improved.
Mathematical Practice 4: Model with mathematics.
In the Challenge Problem, some students may have used one or more rectangular prisms to model the man and approximate his volume. Ask these students to describe how they reasoned about creating their models.
Performance Task
Ways of Thinking: Make Connections
- Take notes about your classmates’ methods for finding the volume of a cube and a rectangular prism.
Hint:
As your classmates present, ask questions such as:
- What problems did you encounter in finding the volume?
- What knowledge of multiplying fractions did you use?
- Did you make an estimate of the volume first? How did you make your estimate?
- How did the Cube Builder help you?
- How do you know your answer is correct?
Volume of Rectangular Prisms
A Possible Summary
You can build a prism with fractional side lengths using unit-fraction cubes. To find the volume of the prism, multiply the number of unit-fraction cubes times the volume of each cube. This gives you the same answer as you would get by using the volume formula V = lwh.
ELL: Give students plenty of wait time as some of them are learning and processing new mathematical information in a second language. Make a chart of the key points that students make during their presentations on volume of rectangular prisms.
Formative Assessment
Summary of the Math: Volume of Rectangular Prisms
- Write a summary about how to build and find the volume of rectangular prisms.
Hint:
Check your summary.
- Do you explain how to build a prism with cubes and find the volume of the prism?
- Do you provide a formula for finding the volume of any rectangular prism?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to see what students like about using the volume formula.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I like using a formula to find volume because …