- Author:
- Chris Adcock
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Cube Builder
Gallery Problems Exercise (Groups)

Overview
Gallery Overview
Students who are caught up can spend this time working on gallery problems while you work with other students in study groups. Students have a choice of problems, and they can work on however many problems time permits.
Gallery Descriptions
Finding the Missing Base
Students will find the length of one of the bases of a trapezoid given the length of the other base, the height, and the area.
Utah Units
Students will estimate the area of Utah and then estimate the area of the United States in “Utah” units.
Growing Rectangles
Students know how to find the lengths of the sides of polygons on the coordinate plane. They will use this knowledge to find the area of each rectangle in a series of growing rectangles.
The Volumes of Solids
Students will find the volume of solids that are built out of cubes. They will also build their own solid out of cubes and have their partner find its volume.
From 3-D to 2-D and Back
Students will investigate the net of a milk carton.
Geometry of Gardening
Students will use their knowledge of perimeter and area to design a garden on grid paper.
Net of a Number Cube
Students will draw a net of a number cube.
Dividing Parallelograms
Students will prove or disprove Emma's statement about dividing parallelograms into four triangles, all with the same area.
Area of Triangles
Students will find the areas of two different triangles on the coordinate plane.
Placing a Rug
Students will place a square rug exactly in the middle of a floor and find the number of square feet not covered by the rug.
Finding the Missing Base
Answers
- The other base has a length of 3.5
- Sketches may vary. Possible sketch:
Work Time
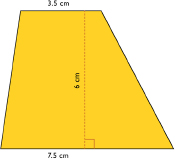
Find the Missing Base
A trapezoid’s height is 67.533.
Use this information and the formula for the area of a trapezoid to calculate the length of the other base. Show your work.
Sketch the trapezoid and label the base lengths and the height.
Utah Units
Answers
- Using the scale, the larger rectangle in the composite area is about 275 mi by about 325 mi. The smaller rectangle is about 75 mi by 100 mi. The area is (275 × 325) – (75 × 100) = 89,375 − 7,500 = 81,875, or about 82,000 mi2.
- The area of the continental United States is about 40 Utahs.
- 40 Utahs x 81,875 mi2 per Utah = 3,275,000
The area of the continental United States is about 3,275,000 square miles.
(Actual areas are approximately 84,900 mi2 for Utah and 3,120,000 mi2 for the continental United States.)
Work Time
Utah Units
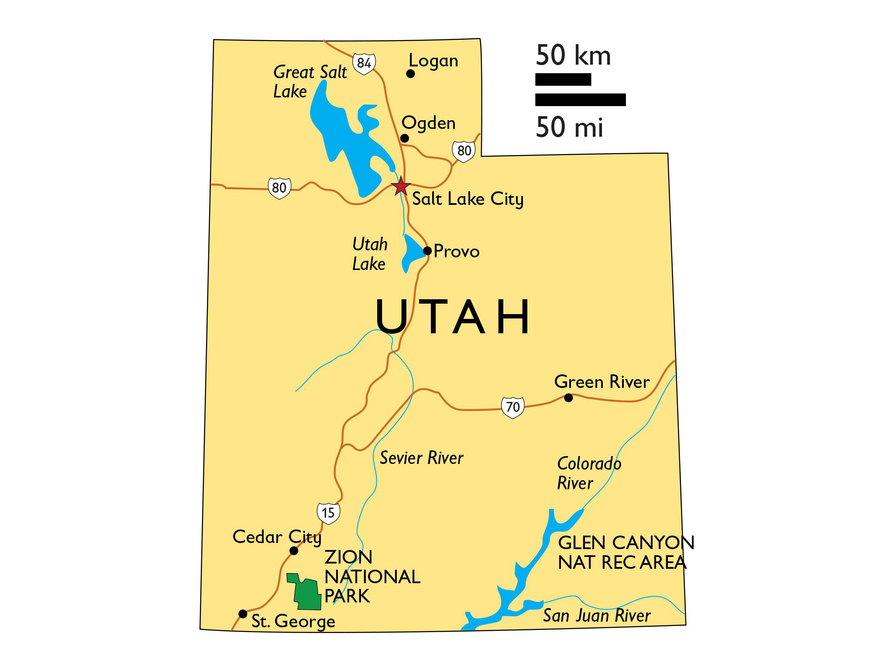
The state of Utah has a rather geometrical shape, as shown in the image.
The shape is close to a rectangle, with a small rectangle cut out of the upper right corner.
- Use the scale to estimate the total area of Utah in square miles.
- Use the area of Utah as a unit of measure to estimate the area of the continental United States. That is, estimate the area of the continental United States in “Utahs.”
- Use your answers to problems 1 and 2 to estimate the area of the continental United States in square miles.
Growing Rectangles
Answers
- The area of rectangle B is 1.5 square units.
The area of rectangle C is 6 square units.
The area of rectangle D is 24 square units.
The area of rectangle E is 96 square units.
- The coordinates of point b are (–1, –1). The coordinates of point c are (1, 0.5). The coordinates of point d are (5, 3.5). The coordinates of point e are (13, 9.5).
- The distance between points and is 15 units.
- The distance from point b to the x-axis is 1 unit.
The distance from point c to the x-axis is 0.5 unit.
The distance from point d to the x-axis is 3.5 units.
The distance from point e to the x-axis is 9.5 units.
- The coordinates of point f are (29, 21.5). The coordinates of point g are (61, 45.5).
- The area of rectangle F is 384 square units. The area of rectangle G is 1,536 square units.
Work Time
Growing Rectangles
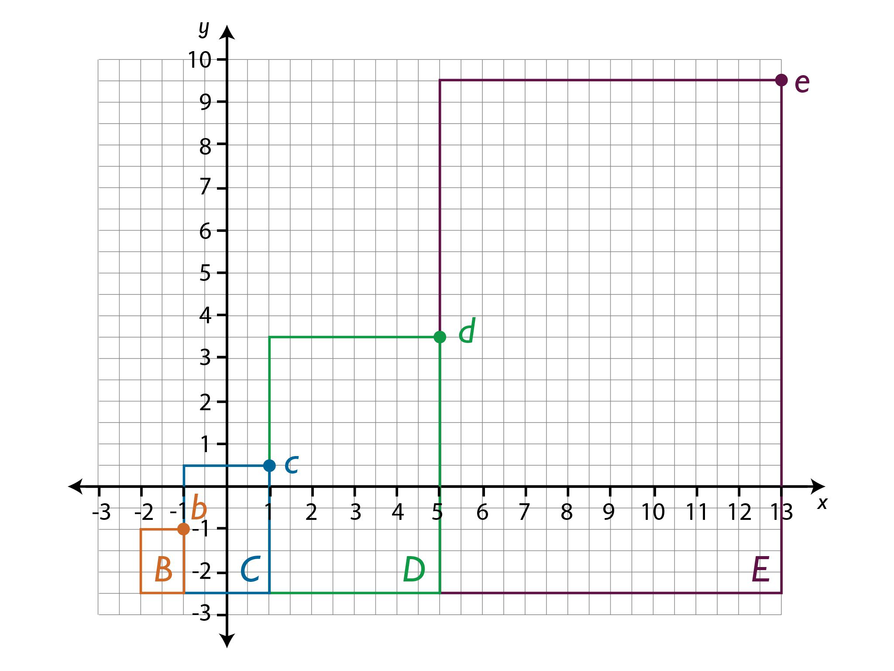
Look at this series of growing rectangles on the right.
Calculate the areas of rectangles B, C, D, and E.
Find the coordinates of the points b, c, d, and e .
What is the distance between points and ?
What is the distance from each of the points b, c, d, and e to the x-axis?
If you continue the series and draw rectangles F and G, what are the coordinates of corresponding points f and g?
What are the areas of rectangles F and G?
The Volume of Solids
Answers
The volume is 96 cubic units.
Possible strategy: Divide the figure into two 8-by-2-by-2 prisms and two 4-by-2-by-2 prisms. The volume then is 2(8 ⋅ 2 ⋅ 2) + 2(4 ⋅ 2 ⋅ 2) = 96, or 96 cubic units.
- The volume is 208 cubic units.
Possible strategy: Divide the figure into an 8-by-5-by-3 prism and two 3-by-2-by-3 prisms. The volume then is (8 ⋅ 5 ⋅ 3) + 2(3 ⋅ 2 ⋅ 3) = 156, or 156 cubic units.
- The volume is 216 cubic units.
Possible strategy: Divide the figure into two 2-by-8-by-4 prisms, one 4-by-4-by-4 cube, and “stair steps” with a 3-by-4 layer, a 2-by-4 layer, and a 1-by-4 layer. The volume then is 2(2 ⋅ 8 ⋅ 4) + (4 ⋅ 4 ⋅ 4) + (3 ⋅ 4) + (2 ⋅ 4) + (1 ⋅ 4) = 216, or 216 cubic units.
- The volume is 56 cubic units.
Possible strategy: The bottom layer is 6 by 6, the middle is 4 by 4, and the top is 2 by 2. The volume then is (6 ⋅ 6) + (4 ⋅ 4) + (2 ⋅ 2) = 56, or 56 cubic units.
- The volume is 204 cubic units.
Possible strategy: Find the number of cubes in each layer and add. The volume then is (8 ⋅ 8) + (7 ⋅ 7) + (6 ⋅ 6) + (5 ⋅ 5) + (4 ⋅ 4) + (3 ⋅ 3) + (2 ⋅ 2) + 1 = 204, or 204 cubic units.
The total surface area is 272 square units.
Possible strategy: Consider one view at a time and count the exposed cube faces:
Front: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Left view: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Right view: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Back view: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Top view: (8 + 7) + (7 + 6) + (6 + 5) + (5 + 4) + (4 + 3) + (3 + 2) + (2 + 1) + 1 = 64
Bottom view: 8 ⋅ 8 = 64
Total surface area = (4 ⋅ 36) + (2 ⋅ 64) = 272
The total surface area is 272 square units.
Answers will vary. Check students' work.
Work Time
The Volume of Solids
- The following solids are all built out of cubes. Find the volume of each solid, and describe your solution strategy.
- Find the total surface area of the last building.
- Make your own building using the Cube Builder, and ask a classmate to find the volume of your building.
INTERCTIVE: Building Viewer
INTERACTIVE: Cube Builder
From 3-D to 2-D and Back
Answers
1 dm3 = 1,000 cm3
7 ⋅ 7 ⋅ h = 1,000
49h = 1,000
h ≈ 20.4The height of the milk carton would have to be about 20.4 cm.
Possible answer: When the net is folded, the triangles at the top form the slanted part of the carton that sticks up. The triangles at the bottom form the flat bottom of the carton.
Drawings will vary.
Possible answer: The vertex angles of the triangles would not be right angles, so the triangles would not fit together as the triangles in problem 3.
Check students' work. One possible carton would have the same base as the liter carton, but with only half the height. The net would be similar to the net for the liter carton, but the length of each of the rectangles would be half what it is in that net.
Work Time
From 3-D to 2-D and Back
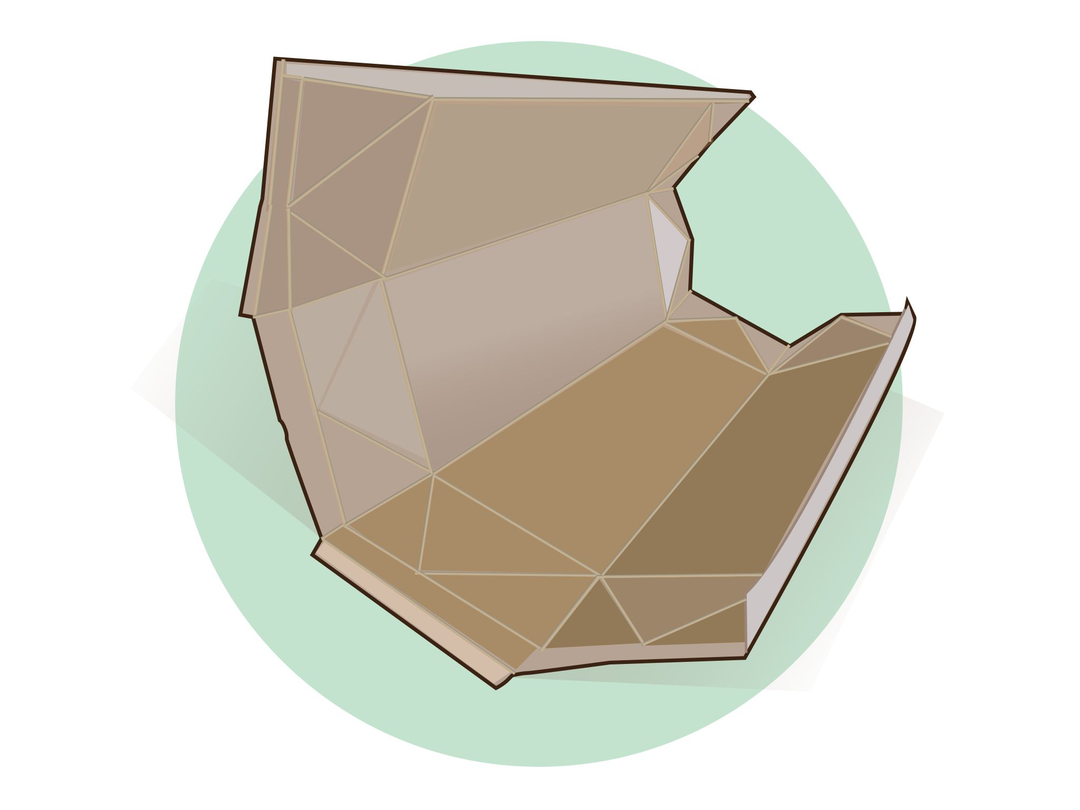
While traveling in the Netherlands, Denzel bought a liter of milk. This image shows what the carton looked like.
This type of carton is constructed to allow a combination of pushing and pulling to make a convenient pour spout.

Denzel cut and unfolded the carton as shown.
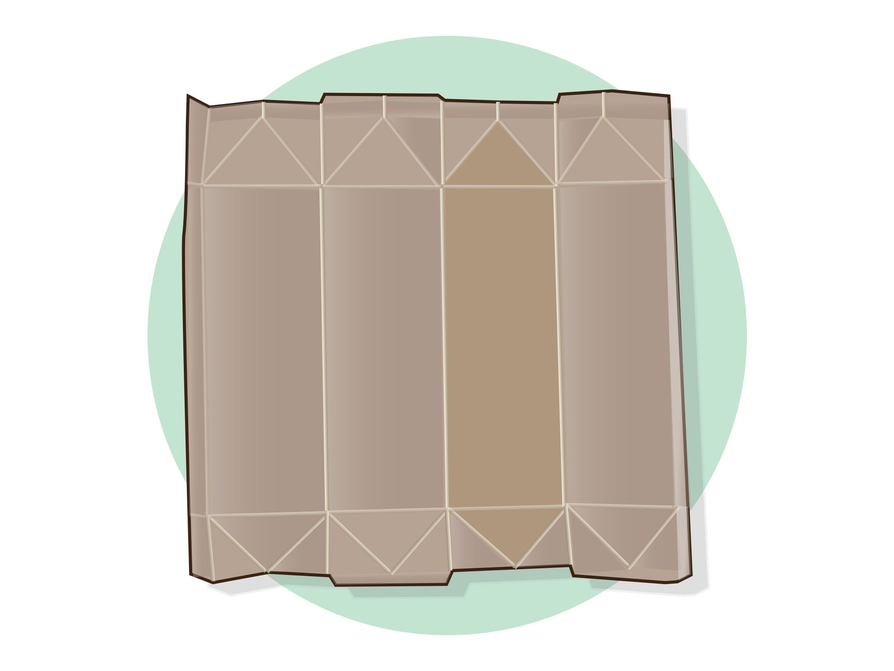
He flattened the carton to get the net shown below.
- The base of the carton is a square with side lengths of 7 centimeters. How high must the carton be to have a volume of 1 liter? (1 liter = 1 cubic decimeter)
- The net for the carton is almost a perfect square with dimensions 29 centimeters by 29 centimeters. The triangles at the top and bottom of the net are what make it possible to transform the square into a milk carton just by folding. Explain why the heights of the triangles that form the top of the carton are taller than the heights of the triangles that form the bottom of the carton.
- The four isosceles triangles at the bottom of the net each have a base length of 7 centimeters and a height of 3.5 centimeters. Draw four isosceles triangles with these dimensions. Cut out the triangles and show that they form a square.
- Explain why four isosceles triangles each with a base length of 7 centimeters and a height of 4 centimeters do not form a square.
- Draw a precise net of a half-liter carton, and build it.
The Geometry of Gardening
Answers
- The garden is a rectangle.
- The coordinates of the fourth corner are .
The area of house's base is 2,500 m2.
The volume of sand needed is 1,250 m3.- Each side of the fence will be 90 m long, so the total length of the fence will be 360 m.
- Area of garden—fenced area = Area of the grass
The area of the grass is 51,900 m2. - Answers will vary. In the example above, the pool has vertices at .
Work Time
Geometry of Gardening
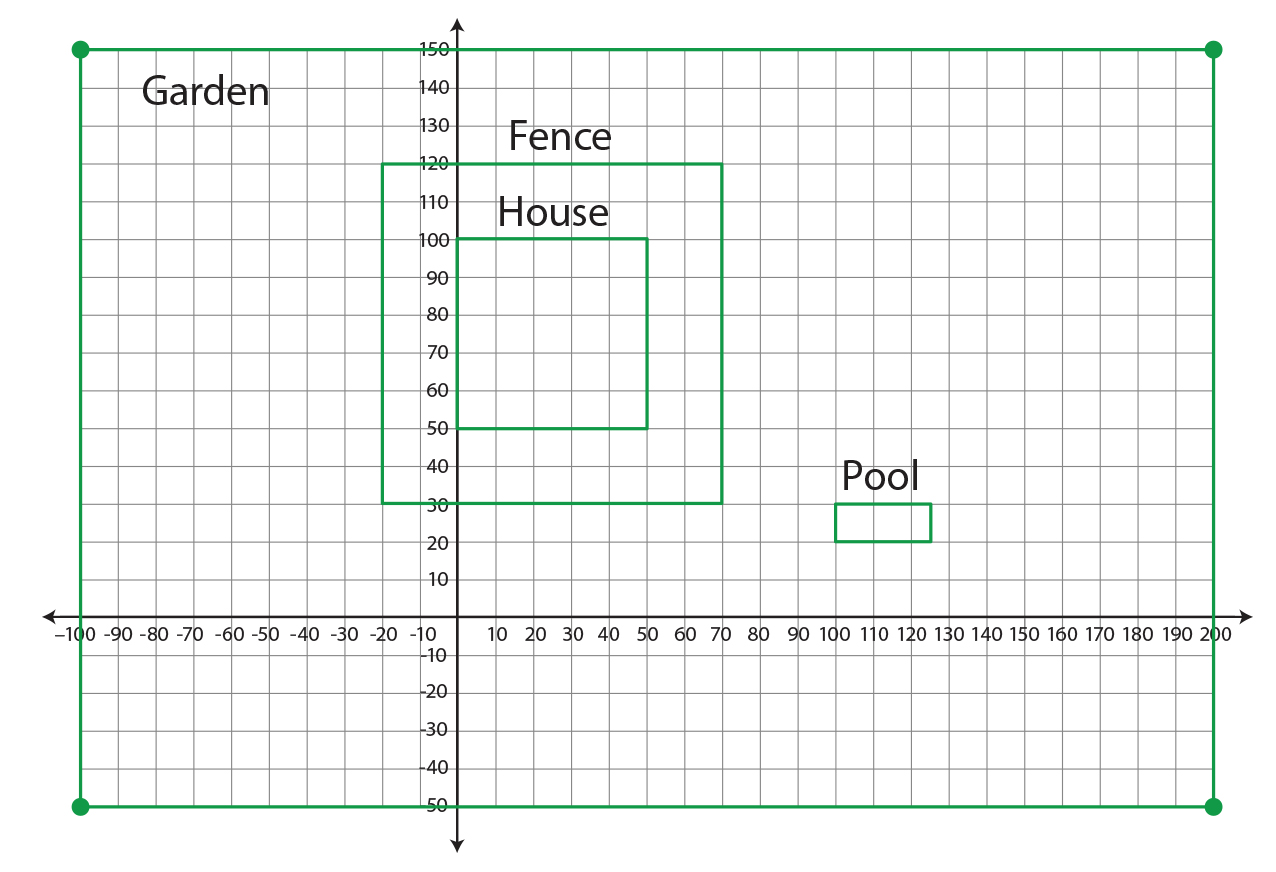
Many gardens have geometrical designs, which often include squares and rectangles, as shown in the image. Gardeners often use grid paper to sketch their designs. Sketch a garden on grid paper. The length of each square on the grid represents 10 meters.
- The coordinates of the corners of the garden are . Plot these points, connecting them in order. What figure is the garden?
- A house with a square base will be built inside the garden area. Three corners of the house have coordinates . What are the coordinates of the fourth corner? What is the area of the house’s base?
- Sand will be used to cover the ground under the house. The layer of sand will be 0.5 meter high. What volume of sand is needed?
- A fence will be built around the house 20 meters away from the house. How long is the fence?
- Outside the fence, grass will be planted. How many square meters is the grassy area?
- Inside the grassy area, a rectangular swimming pool measuring 10 meters by 25 meters will be built. Draw the swimming pool in the grassy area any place you like. What are the coordinates of the corners of this swimming pool?
Net of a Number Cube
Answer
Work Time
Net of a Number Cube
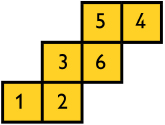
A number cube is a cube with the numbers 1 through 6 labeled on its faces. The numbers on opposite faces add up to 7.
- Draw a net of a number cube.
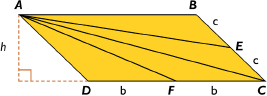
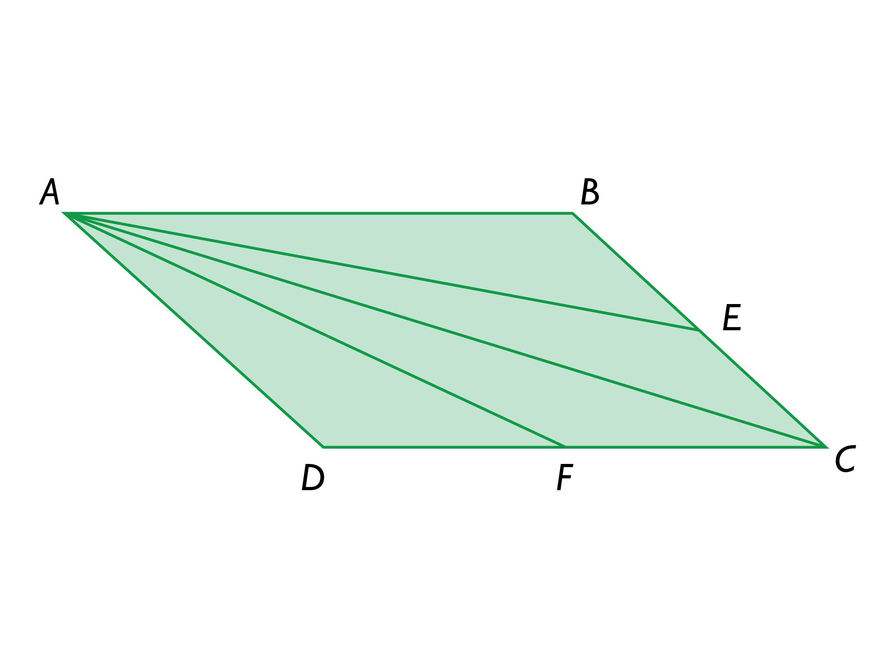
Dividing Parallelograms
Answers
Emma is correct.
The areas of the four triangles must be equal. This must be true for all parallelograms.
Since F is the midpoint of , then . Call those lengths b.
Since E is the midpoint of , then . Call those lengths c.
Since both have a base of length b and height h:
By the same argument, since and both have a base of length c and the same height, their areas must be equal to each other. (Point out that the height is not equal to h unless the parallelogram is a rhombus.)
Since we know that the diagonal of a parallelogram divides the parallelogram into two equal parts, then:
Work Time
Dividing Parallelograms
Emma says that she can divide any parallelogram into four triangles with equal areas using this method:
On parallelogram ABCD, I draw diagonal AC.
Next, I mark the midpoint of line segment BC, which is point E. I draw line segment AE.
Finally, I mark the midpoint of line segment CD, which is point F. I draw line segment AF.
For any parallelogram, these steps result in four triangles with equal areas.
Is Emma right?
State your decision and justify it mathematically—that is, if you think Emma’s method works for any parallelogram, show why it does.
If you think it does not, show why not.
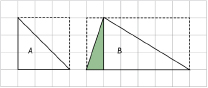
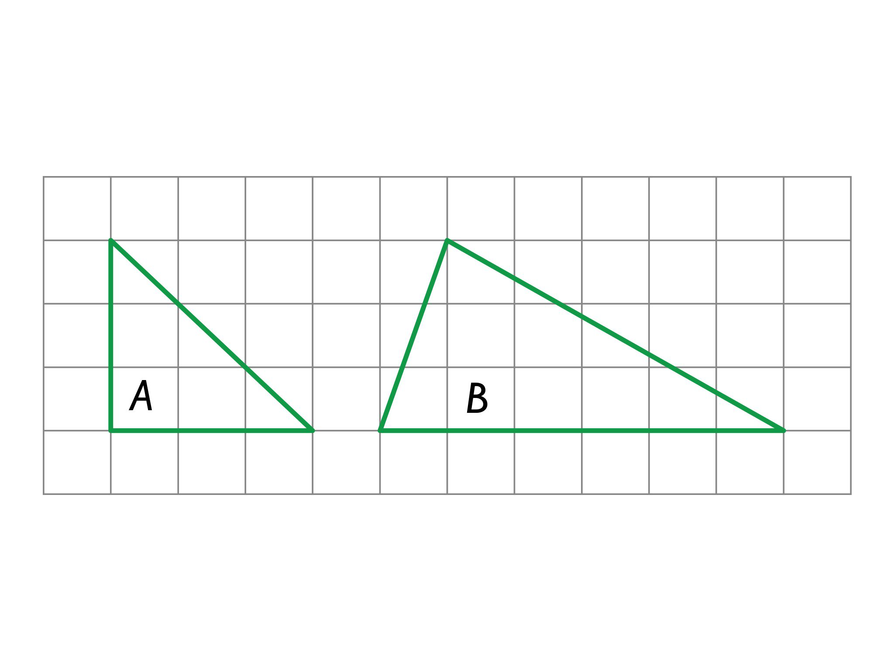
Area of Triangles
Answers
- A is half of a square, so it has a height of 3 units and a base of 3 units.
The area of A is square units.
B can be decomposed into two right triangles.
The shaded part of B is half of a rectangle, so it has a base of 1 unit and a height of 3 units.
The unshaded part of B is half of a rectangle, so it has a base of 5 units and a height of 3 units.
The area of B is 9 square units.
Work Time
Area of Triangles
Find the area of triangle A. Describe step by step the method you used to find its area.
Find the area of triangle B. Describe step by step the method you used to find its area.
Placing a Rug
Answers
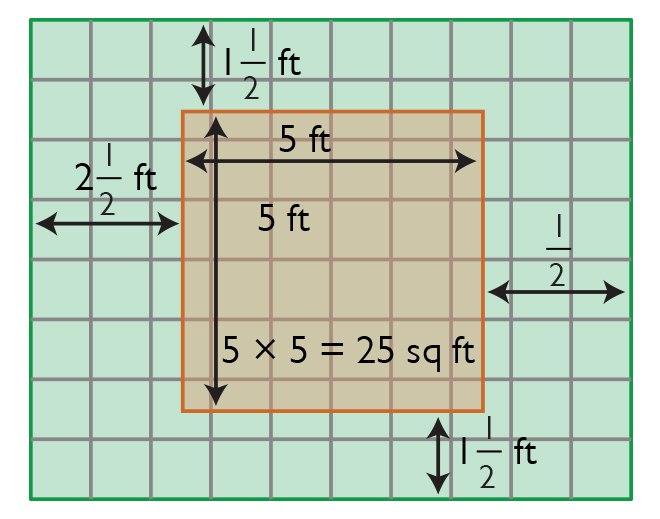
- The rug has an area of 25 ft2. Since it is a square rug, each side has a length of 5 ft (5 × 5 = 25). Since the length of the room is 10 ft, there will be ft of uncovered floor on each end of the room. Since the width of the room is 8 ft, there will be ft on the other ends of the room.
Work Time
Placing a Rug
The image on the right shows a floor plan of Mrs. Thompson’s living room. She wants to put a square rug with an area of 25 square feet exactly in the middle of the floor.
- Shade the floor plan to show where the rug will go.
- Find the number of square feet that will not be covered by the rug.