Basic & Composite Figures

Overview
Lesson Overview
Students use what they know about finding the areas of basic figures to find areas of composite figures.
Key Concepts
A composite figure is a figure that can be divided into two or more basic figures.
The area of a composite figure can be found by dividing it into basic figures whose areas can be calculated easily.
For some figures, the area can also be found by surrounding the figure with a basic figure, creating other basic figures “between” the original figure and the surrounding figure. The area of the original figure can then be found by subtracting the basic figure.
Goals and Learning Objectives
- Find the area of composite figures by decomposing and composing them into more basic figures.
Area of a Figure
Lesson Guide
Explain that this figure is part of a park that is covered with grass.
Partners should discuss strategies for finding the area of this figure.
ELL: When monitoring students, pay special attention to ELLs to ascertain that they are on task and clear about what needs to be done. Some students may not recognize strategies for finding areas for composite figures. Provide direct instruction for struggling students.
Mathematics
Ask:
- How can you break the figure into rectangles or triangles so you can find its area?
- Can you think of another strategy for finding the area?
Opening
Area of a Figure
This figure represents the part of a park that is covered with grass. Discuss the following questions.
- How is the figure composed of other figures?
- How can the figure be decomposed into other figures?
- How can you find the area of this figure?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will compose and decompose figures to find their areas. Review the definitions of compose and decompose if these terms are not familiar to students.
Opening
Compose and decompose figures to find their areas.
A Rectangular Figure
Lesson Guide
Have students compose and decompose figures to find their areas.
Have students work solo on these problems for a few minutes and then have them complete the problems with a partner. Ask partners to prepare the presentation together.
As students work, ask questions such as the following:
- What is your strategy for finding the area of the figure?
- Can you break apart the figure in another way to find the area?
SWD: Have students list the key shapes they see in the composite figure. Encourage students to highlight the triangles, parallelograms, rectangles, and trapezoids they identify. This will assist them in finding the total area.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
Students may want to use a ruler and pencil to divide the figures. Some students may wish to use scissors to cut the figure into parts. Students who cut the figure apart may need to measure to find the lengths. Be sure they understand that 1 cm on the rectangle is equal to 1 m in the park. Students should measure the lengths they need to the nearest half-centimeter to find the area of each part.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who approach finding the areas of the composite figures in different ways. Look for students who decompose the same figure in different ways or for those who take an entirely different approach. Identify students who struggle but stick with the problem until they find a solution.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What figures do you already know how to find the areas of?
- Can you break this figure into those familiar figures?
Student does not break the figure down into the most basic figures.
- Look at the figures you divided the composite figure into. Are they all figures you can find the area of?
- Can you find the area of this figure? If not, can you break it into familiar figures?
Student has an incorrect solution.
- How can you check your work?
- Did you include the area of each part exactly once when you found the total area?
- What if you break apart the figure in a different way? Do you get the same area?
Student has a unique or interesting solution method.
- Why did you approach the problem in the way you did?
- Explain your strategy for solving the problem.
SWD: During Partner Work, monitor student discussions and provide guiding questions from the Interventions to help students see the mathematics and find their own way to a solution. If a student is struggling with a particular concept, hold an individual conference. If many students are struggling with a concept, pull a small group to discuss the concept.
Answers
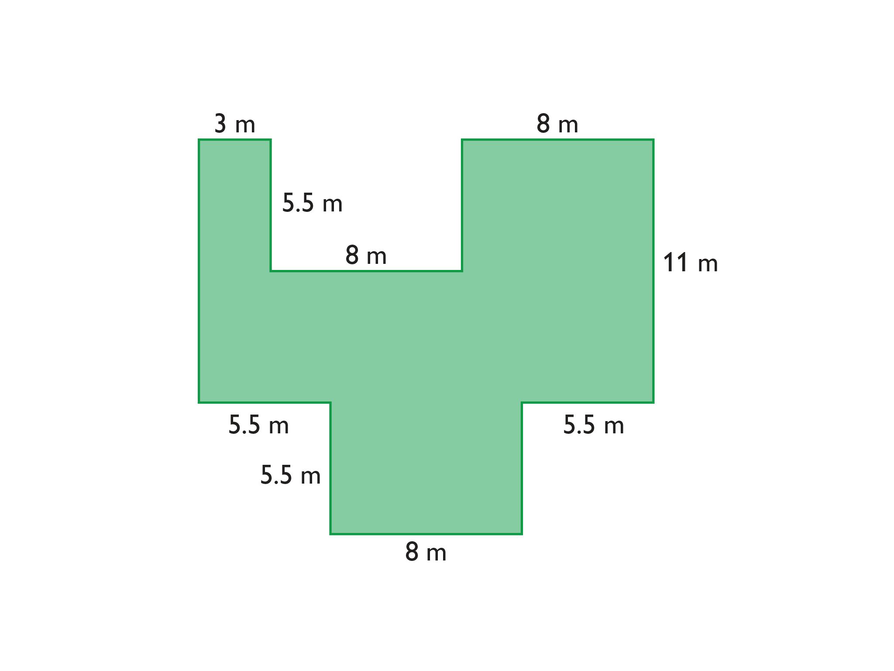
- The area of the figure is 209 m2.
Work Time
A Rectangular Figure
This figure is an example of a composite figure. A composite figure is a figure that can be broken into two or more basic figures. It is composed of basic figures and can be decomposed into basic figures.
- Find the area of this composite figure.
Hint:
- Can you decompose the composite figure into basic figures that you already know how to find the area of?
- Or, can you draw a familiar figure around the composite figure and use subtraction to find the area of the composite figure?
A Mixed Figure
Lesson Guide
Have students compose and decompose figures to find their areas.
Have students work solo on these problems for a few minutes and then have them complete the problems with a partner. Ask partners to prepare the presentation together.
As students work, ask questions such as the following:
- What is your strategy for finding the area of the figure?
- Can you break apart the figure in another way to find the area?
SWD: Have students list the key shapes they see in the composite figure. Encourage students to highlight the triangles, parallelograms, rectangles, and trapezoids they identify. This will assist them in finding the total area.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
Students may want to use a ruler and pencil to divide the figures. Some students may wish to use scissors to cut the figure into parts. Students who cut the figure apart may need to measure to find the lengths. Be sure they understand that 1 cm on the rectangle is equal to 1 m in the park. Students should measure the lengths they need to the nearest half-centimeter to find the area of each part.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who approach finding the areas of the composite figures in different ways. Look for students who decompose the same figure in different ways or for those who take an entirely different approach. Identify students who struggle, but stick with the problem until they find a solution.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What figures do you already know how to find the areas of?
- Can you break this figure into those familiar figures?
Student does not break the figure down into the most basic figures.
- Look at the figures you divided the composite figure into. Are they all figures you can find the area of?
- Can you find the area of this figure? If not, can you break it into familiar figures?
Student has an incorrect solution.
- How can you check your work?
- Did you include the area of each part exactly once when you found the total area?
- What if you break apart the figure in a different way? Do you get the same area?
Student has a unique or interesting solution method.
- Why did you approach the problem in the way you did?
- Explain your strategy for solving the problem.
Answers
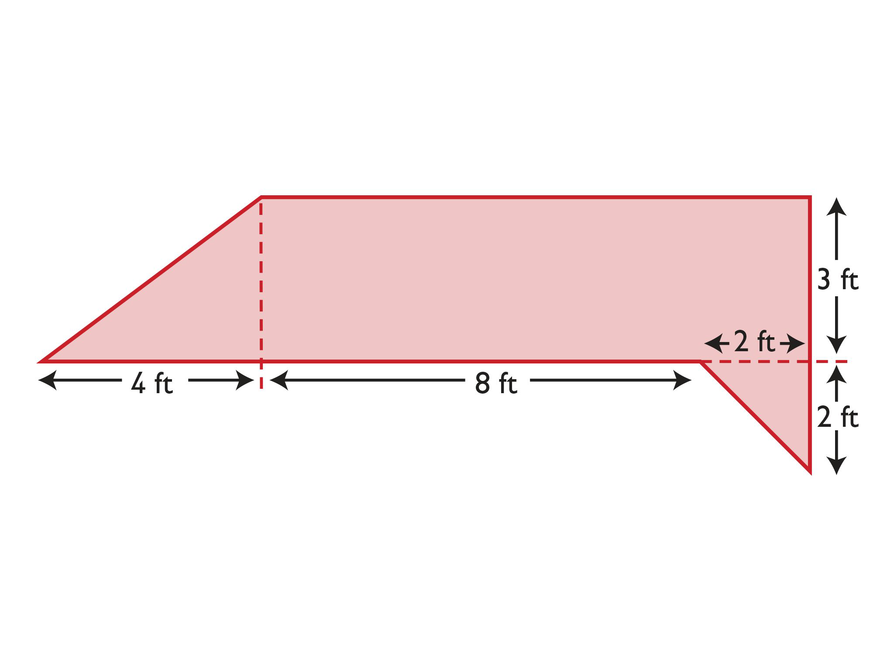
- The area of the figure is 38 ft2.
Work Time
A Mixed Figure
- Find the area of this composite figure.
Hint:
- Can you decompose the composite figure into basic figures that you already know how to find the area of?
- Or, can you draw a familiar figure around the composite figure and use subtraction to find the area of the composite figure?
A Triangular Figure
Lesson Guide
Have students compose and decompose figures on the tablet to find their areas.
Have students work solo on these problems for a few minutes and then have them complete the problems with a partner. Ask partners to prepare the presentation together.
As students work, ask questions such as the following:
- What is your strategy for finding the area of the figure?
- Can you break apart the figure in another way to find the area? SWD:
Have students list the key shapes they see in the composite figure. Encourage students to highlight the triangles, parallelograms, rectangles, and trapezoids they identify. This will assist them in finding the total area.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
Students may want to use a ruler and pencil to divide the figures. Some students may wish to use scissors to cut the figure into parts. Students who cut the figure apart may need to measure to find the lengths. Be sure they understand that 1 cm on the rectangle is equal to 1 m in the park. Students should measure the lengths they need to the nearest half-centimeter to find the area of each part.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who approach finding the areas of the composite figures in different ways. Look for students who decompose the same figure in different ways or for those who take an entirely different approach. Identify students who struggle, but stick with the problem until they find a solution.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What figures do you already know how to find the areas of?
- Can you break this figure into those familiar figures?
Student does not break the figure down into the most basic figures.
- Look at the figures you divided the composite figure into. Are they all figures you can find the area of?
- Can you find the area of this figure? If not, can you break it into familiar figures?
Student has an incorrect solution.
- How can you check your work?
- Did you include the area of each part exactly once when you found the total area?
- What if you break apart the figure in a different way? Do you get the same area?
Student has a unique or interesting solution method.
- Why did you approach the problem in the way you did?
- Explain your strategy for solving the problem.
SWD: During partner work, monitor student discussions and provide guiding questions from the Interventions to help students see the mathematics and find their own way to a solution. If a student is struggling with a particular concept, hold an individual conference. If many students are struggling with a concept, pull a small group to discuss the concept.
Answers
- The area of the figure is 0.165 ft2.
Work Time
A Triangular Figure
- Find the area of this composite figure.
Hint:
- The mark on the two side lengths means that they are the same length.
- Can you decompose the composite figure into basic figures that you already know how to find the area of?
- Or can you draw a familiar figure around the composite figure and use subtraction to find the area of the composite figure?
Prepare a Presentation
Preparing for Ways of Thinking
Identify students with different solution methods to share during Ways of Thinking:
- Students who decompose the original figure into different basic figures and then find and add their areas
- Students who surround the original figure with a basic figure and then subtract the area of the basic figures formed between the surrounding figure and the original figure
- [common error] Watch for students who decompose the figure correctly, but make a mistake when combining the areas. Students may leave out the area of one or more of the basic figures or count the area of a basic figure twice. Encourage students to write an addition expression for the total area with an addend for each basic figure. Before doing the addition, students should count to make sure the number of addends matches the number of basic figures.
ELL: Encourage students to use diagrams, if necessary, to explain how they found the area. It is important that you provide an environment in which all students feel comfortable sharing their solutions.
SWD: Students must feel safe enough to share their ideas, strategies, and, most importantly, mistakes. Most students—and students with disabilities in particular—are not used to talking about mathematics; yet in higher-level courses, student success might depend on participation in study groups and the student's ability to share ideas.
Challenge Problem
Answers
- Answers will vary. Check students' figures and areas.
Work Time
Prepare a Presentation
- Explain how you find areas of composite figures. Use your work to support your explanation.
Challenge Problem
- Draw a composite figure and find its area.
Make Connections
Mathematics
Have students share the different ways they decomposed the figures and found their areas.
For the first figure, there are many ways to decompose it into rectangles. Here is one possibility:
Another strategy is to sketch a rectangle around the figure and subtract the areas of the white rectangles (A, B, and C in the figure below) from the area of the surrounding rectangle.
Ask:
- Even though we broke up the figures in different ways, did we get the same area for each figure?
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Have students critique and compare the different methods used by the class for various figures and discuss which methods seem to be the easiest or more efficient.
Performance Task
Ways of Thinking: Make Connections
- Take notes about other classmates' approaches to finding the areas. How are the approaches similar to your approach? How are they different?
Hint:
As your classmates present, ask questions such as:
- How did you decompose the figure?
- How did you find the base and height for the figure?
- For which figure did you have the most difficulty finding the area?
- What formula did you use?
- How did you know to use that formula?
Methods for Finding Area
Mathematics
Have pairs quietly discuss how they can use the area of a triangle and the area of a rectangle to determine the area of all polygons. Have pairs use the methods described to find the area of a few polygons, both regular and irregular.
As student pairs work together, listen for students who may still have misconceptions so you can address them in the class discussion.
After a few minutes, discuss the summary as a class. Have volunteers share their methods for finding the areas of polygons. Include both regular and irregular polygons in the examples. Then summarize the following points:
- You can find the area of any polygon by breaking it into triangles and rectangles.
- Sometimes you can surround the polygon with a rectangle or another basic figure and subtract to find the area of the composite figure.
Formative Assessment
Summary of the Math: Methods for Finding Area
Read and Discuss
- Knowing the formulas for the area of a triangle and the area of a rectangle allows you to determine the area of all other polygons, regular and irregular.
- For parallelograms and trapezoids, you can find the area by decomposing the polygon into combinations of right triangles and rectangles and then adding the areas of the component shapes.
- For other polygons, a good method to use is to first construct any one diagonal of the polygon. Then join each of the other vertices to the diagonal with perpendicular line segments. Decompose any trapezoids that are formed in this process into rectangles and right triangles and then find the areas of the component shapes.
- You can also draw a familiar figure around the composite figure and use subtraction to find the area of the composite figure.
Hint:
Can you:
- Find the areas of composite figures?
- Give examples to illustrate your strategies for finding the areas of composite figures?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students learned about finding the area of composite figures.
ELL: When writing the reflection, allow additional time for ELLs to discuss with a partner before writing to help them organize their thoughts. Allow ELLs who share the same primary language to discuss in that language if they prefer, and to use a dictionary.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
The way I found the area of one of the composite figures was …