
Learn about vectors and scalars in physics, and find out how they are related to distance and displacement. [5:19]
- Subject:
- Science
- Material Type:
- Audio/Video
- Provider:
- Sophia Learning
- Date Added:
- 12/01/2023

Learn about vectors and scalars in physics, and find out how they are related to distance and displacement. [5:19]

Students learn about video motion capture technology, becoming familiar with concepts such as vector components, magnitudes and directions, position, velocity, and acceleration. They use a (free) classroom data collection and processing tool—the ARK Mirror—to visualize and record 3-D motion. The Augmented Reality Kinematics (ARK) Mirror software collects data via a motion detector. Using an Orbbec Astra Pro 3D camera or Microsoft Kinect (see note below), students can visualize and record a robust set of data and interpret them using statistical and graphical methods. This lesson introduces students to just one possible application of the ARK Mirror software—in the context of a high school physics class. Note: The ARK Mirror is ported to operate on an Orbbec platform. It may also be used with a Microsoft Kinect, although that Microsoft hardware has been discontinued. Refer to the Using ARK Mirror and Microsoft Kinect attachment for how to use the ARK MIrror software with Microsoft Kinect.

In this interactive math game, students use absolute value to determine how many feet below sea level Carl must be to stay away from the shark.
Students explore methods employing simple machines likely used in ancient pyramid building, as well as common modern-day material transportation. They learn about the wheel and axle as a means to transport materials from rock quarry to construction site. They also learn about different types and uses of a lever for purposes of transport. In an open-ended design activity, students choose from everyday materials to engineer a small-scale cart and lever system to convey pyramid-building materials.

Students measure the relative intensity of a magnetic field as a function of distance. They place a permanent magnet selected distances from a compass, measure the deflection, and use the gathered data to compute the relative magnetic field strength. Based on their findings, students create mathematical models and use the models to calculate the field strength at the edge of the magnet. They use the periodic table to predict magnetism. Finally, students create posters to communicate the details their findings. This activity guides students to think more deeply about magnetism and the modeling of fields while practicing data collection and analysis. An equations handout and two grading rubrics are provided.
Students learn about slope, determining slope, distance vs. time graphs through a motion-filled activity. Working in teams with calculators and CBL motion detectors, students attempt to match the provided graphs and equations with the output from the detector displayed on their calculators.


Rate
Type of Unit: Concept
Prior Knowledge
Students should be able to:
Solve problems involving all four operations with rational numbers.
Understand quantity as a number used with a unit of measurement.
Solve problems involving quantities such as distances, intervals of time, liquid volumes, masses of objects, and money, and with the units of measurement for these quantities.
Understand that a ratio is a comparison of two quantities.
Write ratios for problem situations.
Make and interpret tables, graphs, and diagrams.
Write and solve equations to represent problem situations.
Lesson Flow
In this unit, students will explore the concept of rate in a variety of contexts: beats per minute, unit prices, fuel efficiency of a car, population density, speed, and conversion factors. Students will write and refine their own definition for rate and then use it to recognize rates in different situations. Students will learn that every rate is paired with an inverse rate that is a measure of the same relationship. Students will figure out the logic of how units are used with rates. Then students will represent quantitative relationships involving rates, using tables, graphs, double number lines, and formulas, and they will see how to create one such representation when given another.
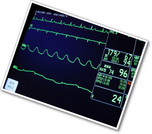
Gallery OverviewAllow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.Gallery DescriptionsCreate Your Own RateStudents create their own rate problems, given three quantities that must all be used in the problems or the answers.Paper Clip ChallengeStudents think about rate in the context of setting a record for making a paperclip chain.The Speed of Light Students must determine the speed of light so they can figure out how long it will take a light beam from Earth to reach the Moon (assuming it would make it there). They conduct research and perform calculations.Tire WeightStudents connect area and a rate they may not be familiar with, tire pressure, to indirectly weigh a car. They find and add areas and do a simple rate calculation. Please note this problem requires adult supervision for the process of measuring the car tires. If no adult supervision is available, you can provide students with measurements to work with inside the classroom. Do not allow students to work with a car without permission from the owner and adult supervision.Planting Wildflowers Students apply area and length concepts (square miles, acres, and feet) to rectangles, choose and carry out appropriate area conversions, and show each step of their solutions. While specific solution paths will vary, all students who show good conceptualization will make at least one area conversion and show understanding about area even when dimensions and units change. This task allows several different correct solution paths.Train Track Students use information about laying railroad ties for the Union Pacific Railroad. These rates are different from those used elsewhere in the unit, asking how many rails per gang of workers, how long it takes to lay one mile of track, and how many spikes are needed for a mile of track.HeartbeatsStudents will investigate and compare the heartbeats of different animals and their own heartbeat.FoghornStudents use the relationships among seconds, minutes, and hours to find equivalent rates. Each step requires students to express an equivalent rate in terms of these different units of time. In any strong response, students use conversion factors and the given rate to find equivalent rates.

In this lesson, students first watch three racers racing against each other. The race is shown on a track and represented on a graph. Students then change the speed, distance, and time to create a race with different results. They graph the new race and compare their graph to the original race graph.Key ConceptsA rate situation can be represented by a graph. Each point on a graph represents a pair of values. In today's situation, each point represents an amount of time and the distance a racer traveled in that amount of time. Time is usually plotted on the horizontal axis. The farther right a point is from the origin, the more time has passed from the start. Distance is usually plotted on the vertical axis. The higher up a point is from the origin, the farther the snail has traveled from the start. A graph of a constant speed is a straight line. Steeper lines show faster speeds.Goals and Learning ObjectivesUnderstand that a graph can be a visual representation of an actual rate situation.Plot pairs of related values on a graph.Use graphs to develop an understanding of rates.

In this lesson, students watch a video of a runner and express his speed as a rate in meters per second. Students then use the rate to determine how long it takes the runner to go any distance.Key ConceptsSpeed is a rate that is expressed as distance traveled per unit of time. Miles per hour, laps per minute, and meters per second are all examples of units for speed. The measures of speed, distance, and time are all related. The relationship can be expressed in three ways: d = rt, r = dt, t = dr.Goals and Learning ObjectivesExplore speed as a rate that measures the relationship between two aspects of a situation: distance and time.In comparing distance, speed, and time, understand how to use any two of these measures to find the third measure.

Students use their knowledge of rates to solve problems.Key ConceptsGiven any two values in a rate situation, you can find the third value.These three equations are equivalent, and they all describe rate relationships:y = rx, r = yx, x = yrAt the beginning of this lesson (or for homework), students will revise their work on the pre-assessment Self Check. Their revised work will provide data that you and your students can use to reassess students' understanding of rate. You can use this information to clear up any remaining misconceptions and to help students integrate their learning from the past several days into a deeper and more coherent whole.The work students do in this lesson and in revising their pre-assessments will help you and your students decide how to help them during the Gallery. In this lesson, students will reveal the depth and clarity of their understanding of rate.Students whose understanding of rate is still delicate should get extra help during the Gallery.Students who feel that they have a robust understanding of rate may choose from any of the problem-solving or deeper mathematics problems in the Gallery.Goals and Learning ObjectivesUncover any partial understandings and misconceptions about rate.Develop a more robust understanding of rate.Identify which Gallery problems to work on.

Proportional Relationships
Type of Unit: Concept
Prior Knowledge
Students should be able to:
Understand what a rate and ratio are.
Make a ratio table.
Make a graph using values from a ratio table.
Lesson Flow
Students start the unit by predicting what will happen in certain situations. They intuitively discover they can predict the situations that are proportional and might have a hard time predicting the ones that are not. In Lessons 2–4, students use the same three situations to explore proportional relationships. Two of the relationships are proportional and one is not. They look at these situations in tables, equations, and graphs. After Lesson 4, students realize a proportional relationship is represented on a graph as a straight line that passes through the origin. In Lesson 5, they look at straight lines that do not represent a proportional relationship. Lesson 6 focuses on the idea of how a proportion that they solved in sixth grade relates to a proportional relationship. They follow that by looking at rates expressed as fractions, finding the unit rate (the constant of proportionality), and then using the constant of proportionality to solve a problem. In Lesson 8, students fine-tune their definition of proportional relationship by looking at situations and determining if they represent proportional relationships and justifying their reasoning. They then apply what they have learned to a situation about flags and stars and extend that thinking to comparing two prices—examining the equations and the graphs. The Putting It Together lesson has them solve two problems and then critique other student work.
Gallery 1 provides students with additional proportional relationship problems.
The second part of the unit works with percents. First, percents are tied to proportional relationships, and then students examine percent situations as formulas, graphs, and tables. They then move to a new context—salary increase—and see the similarities with sales taxes. Next, students explore percent decrease, and then they analyze inaccurate statements involving percents, explaining why the statements are incorrect. Students end this sequence of lessons with a formative assessment that focuses on percent increase and percent decrease and ties it to decimals.
Students have ample opportunities to check, deepen, and apply their understanding of proportional relationships, including percents, with the selection of problems in Gallery 2.

Students determine whether a relationship between two quantities that vary is a proportional relationship in three different situations: the relationship between the dimensions of the actual Empire State Building and a miniature model of the building; the relationship between the distance and time to travel to an amusement park; and the relationship between time and temperature at an amusement park.Key ConceptsWhen the ratio between two varying quantities remains constant, the relationship between the two quantities is called a proportional relationship. For a ratio A:B, the proportional relationship can be described as the collection of ratios equivalent to A:B, or cA:cB, where c is positive.Goals and Learning ObjectivesIdentify proportional relationships.Explain why a situation represents a proportional relationship or why it does not.Determine missing values in a table of quantities based on a proportional relationship.

Putting Math to Work
Type of Unit: Problem Solving
Prior Knowledge
Students should be able to:
Solve problems involving all four operations with rational numbers.
Write ratios and rates.
Write and solve proportions.
Solve problems involving scale.
Write and solve equations to represent problem situations.
Create and interpret maps, graphs, and diagrams.
Use multiple representations (i.e., tables, graphs, and equations) to represent problem situations.
Calculate area and volume.
Solve problems involving linear measurement.
Lesson Flow
Students apply and integrate math concepts they have previously learned to solve mathematical and real-world problems using a variety of strategies. Students have opportunities to explore four real-world situations involving problem solving in a variety of contexts, complete a project of their choice, and work through a series of Gallery problems.
First, students utilize their spatial reasoning and visualization skills to find the least number of cubes needed to construct a structure when given the front and side views. Then, students select a project to complete as they work through this unit to refine their problem-solving skills. Students explore the relationship between flapping frequency, amplitude, and cruising speed to calculate the Strouhal number of a variety of flying and swimming animals. After that, students explore the volume of the Great Lakes, applying strategies for solving volume problems and analyzing diagrams. Next, students graphically represent a virtual journey through the locks of the Welland Canal, estimating the amount of drop through each lock and the distance traveled. Students have a day in class to work on their projects with their group.
Then, students have two days to explore Gallery problems of their choosing. Finally, students present their projects to the class.

Students first create a diagram that represents the distance a ship drops in each of a series of locks. Students create their diagrams based on a video of an actual ship traveling through the locks. Students need to use contextual clues in order to determine the relative drops in each of the locks.Key ConceptsStudents are expected to use the mathematical skills they have acquired in previous lessons or in previous math courses. The lessons in this unit focus on developing and refining problem-solving skills.Students will:Try a variety of strategies to approaching different types of problems.Devise a problem-solving plan and implement their plan systematically.Become aware that problems can be solved in more than one way.See the value of approaching problems in a systematic manner.Communicate their approaches with precision and articulate why their strategies and solutions are reasonable.Make connections between previous learning and real-world problems.Create efficacy and confidence in solving challenging problems in a real-world setting.Goals and Learning ObjectivesRead and interpret maps, graphs, and diagrams.Solve problems that involve linear measurement.Estimate length.Critique a diagram.

Working With Rational Numbers
Type of Unit: Concept
Prior Knowledge
Students should be able to:
Compare and order positive and negative numbers and place them on a number line.
Understand the concepts of opposites absolute value.
Lesson Flow
The unit begins with students using a balloon model to informally explore adding and subtracting integers. With the model, adding or removing heat represents adding or subtracting positive integers, and adding or removing weight represents adding or subtracting negative integers.
Students then move from the balloon model to a number line model for adding and subtracting integers, eventually extending the addition and subtraction rules from integers to all rational numbers. Number lines and multiplication patterns are used to find products of rational numbers. The relationship between multiplication and division is used to understand how to divide rational numbers. Properties of addition are briefly reviewed, then used to prove rules for addition, subtraction, multiplication, and division.
This unit includes problems with real-world contexts, formative assessment lessons, and Gallery problems.

This is a "three star" geometry problem where prior math problem skills and proof experience is recommended to solve this relationship between the inverses of heights.

Look at the changes in results on some of the athletics track events at the Olympic Games in 1908 and 1948. What will the results be in 2012? This slightly more challenging activity encourages children to examine data and consider different kinds of influencing factors, and is designed to be accessible to primary pupils at Key Stage 2.