- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Calculating The Five-Number Summary & Interquartile Range (IQR)

Overview
Students make a box plot for their typical-sixth-grader data from Lesson 7 and write a summary of what the plot shows.
Using the line plot from Lesson 4, students construct a box plot. Students learn how to calculate the five-number summary and interquartile range (IQR). Students apply this knowledge to the data used in Lesson 7 and describe the data in terms of the box plot. Class discussion focuses on comparing the two graphs and what they show for the sets of data.
Key Concepts
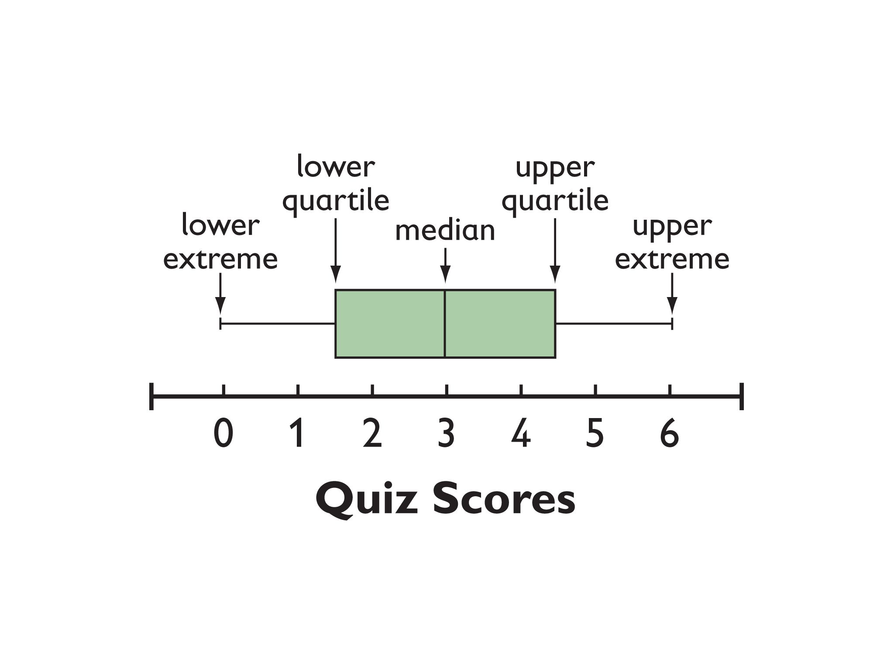
A box-and-whisker plot, or box plot, shows the spread of a set of data. It shows five key measures, called the five-number summary.
- Lower extreme: The smallest value in the data set
- Lower quartile: The middle of the lower half of the data, and the value that 25% of the data fall below
- Median: The middle of the data set
- Upper quartile: The middle of the upper half of the data, and the value that 25% of the data are above
- Upper extreme: The greatest value in the data set
This diagram shows how these values relate to the parts of a box plot.
The length of the box represents the interquartile range (IQR), which is the difference between the lower and upper quartile.
A box plot divides the data into four equal parts. One quarter of the data is represented by the left whisker, two quarters by each half of the box, and one quarter by the right whisker. If one of these parts is long, the data in that quarter are spread out. If one of these quarters is short, the data in that quarter are clustered together.
Goals and Learning Objectives
- Learn how to construct box plots, another tool to describe data.
- Learn about the five-number summary, interquartile range, and how they are related to box plots.
- Compare a line plot and box plot for the same set of data.
Introduction to Box Plots
Lesson Guide
Have students read about drawing a box plot and the five number summary.
SWD: Students have learned and retained information from prior learning experiences, but do not realize when to use that information. Teachers need to remind students of what they know, but also when to apply that knowledge. This strategy is sometimes referred to as “priming” background information. Priming background knowledge can be done in simple ways, such as merely stating “Remember when we learned…” or “See how this concept applies in this situation, too?” It may also involve a more intensive overview of a topic.
Go over the mathematical language used throughout the module. Make sure students use that language when discussing the problems. Provide important vocabulary on an anchor chart in a prominent location in the classroom.
Opening
Introduction to Box Plots
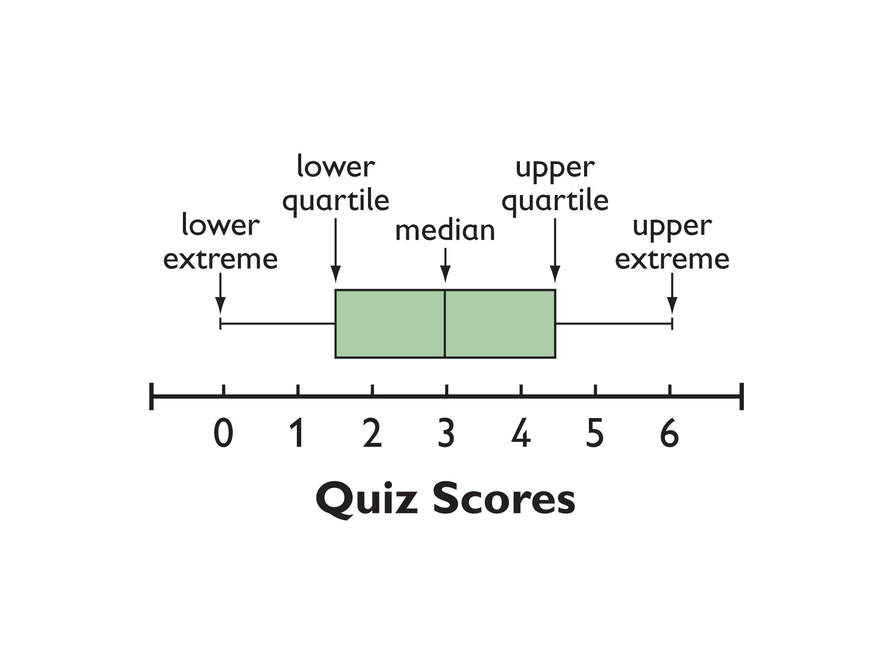
This image shows a box-and-whisker plot (or just a box plot).
Discuss the following information with your partner.
- To draw a box plot you need to know five numbers, called the five-number summary:
- Lower extreme: The least value in the set of data
- Lower quartile: The middle of the lower half of the data
- Median: The middle value
- Upper quartile: The middle of the upper half of the data
- Upper extreme: The greatest value in the set of data
- The box part of a box plot shows the spread of the middle 50 percent of the data. The length of the box is called the interquartile range and represents the distance between the upper and lower quartiles.
Quiz Scores
Lesson Guide
Explain that today students will learn to make a new type of graph that is about measures of spread. Allow students some time to think about how the five-number summary and box plot are related.
Mathematics
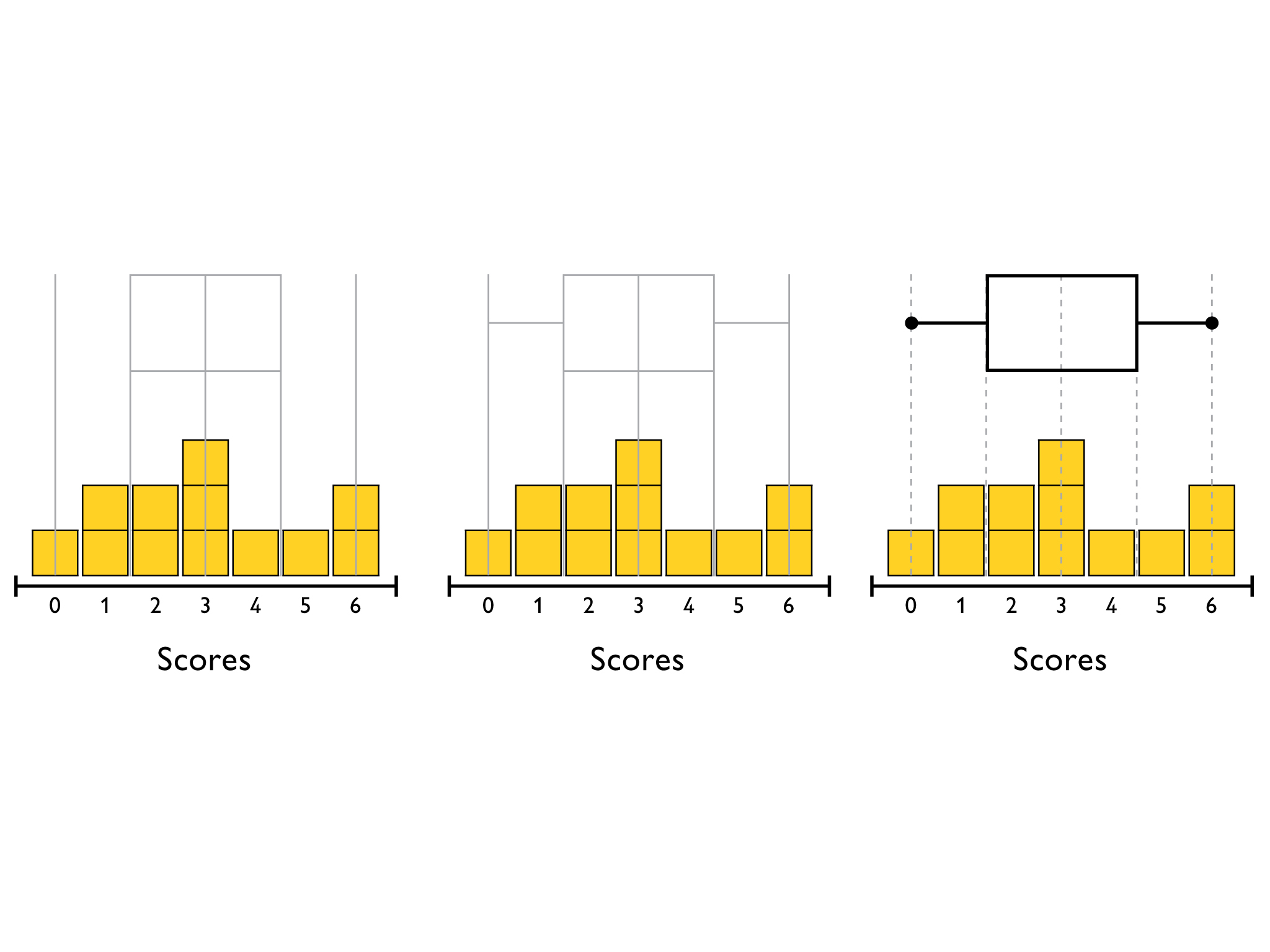
Ask students to think about what the box plot shows, giving them a few minutes to discuss with a partner. Elicit from the students that the data has been divided into quarters (quartiles):
- The lowest quarter of the data is from the lower extreme to the lower quartile.
- The second quarter of the data is from the lower quartile to the median. Altogether half, or 50%, of the data is below the median.
- The third quarter is from the median to the upper quartile.
- The last quarter is from the upper quartile to the upper extreme. The second half of the data is the two quarters above the median.
The width of the box is called the interquartile range (IQR). It is the difference between the lower and upper quartiles. Since the box contains the second and third quarters of the data, this is the middle 50%.
Review the text in the student material, which shows how to find the lower and upper quartiles from an ordered list of data.
Opening
Quiz Scores
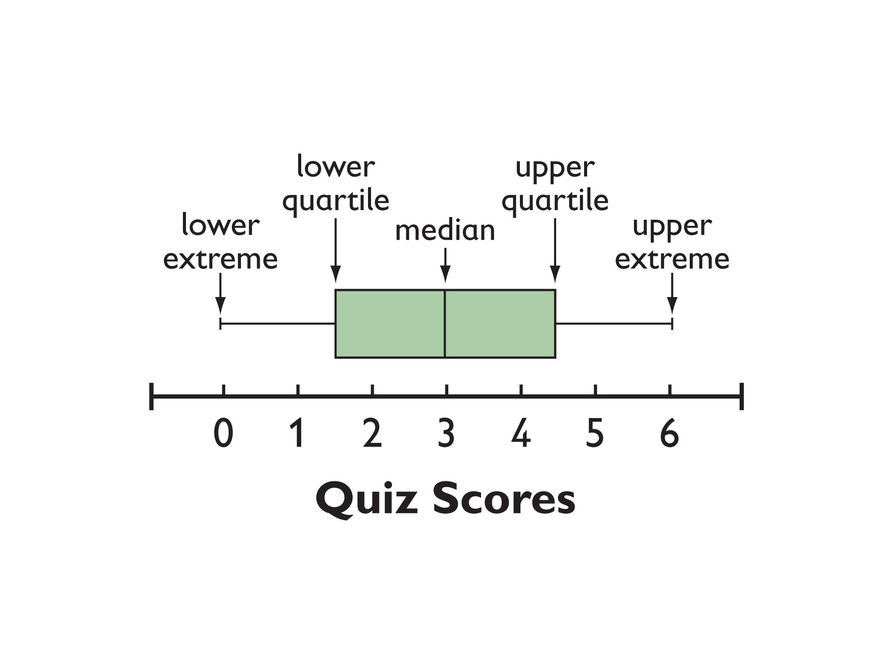
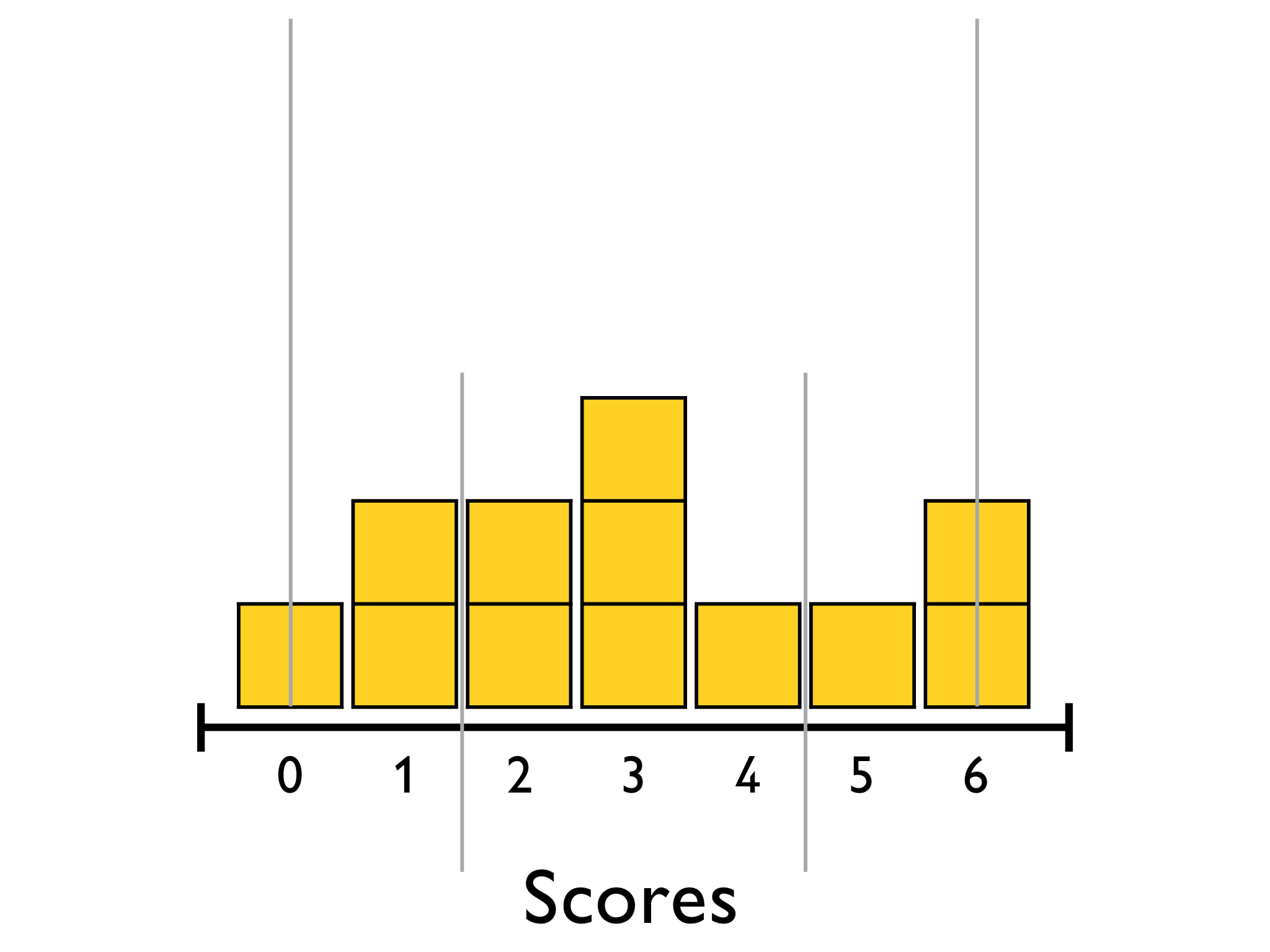
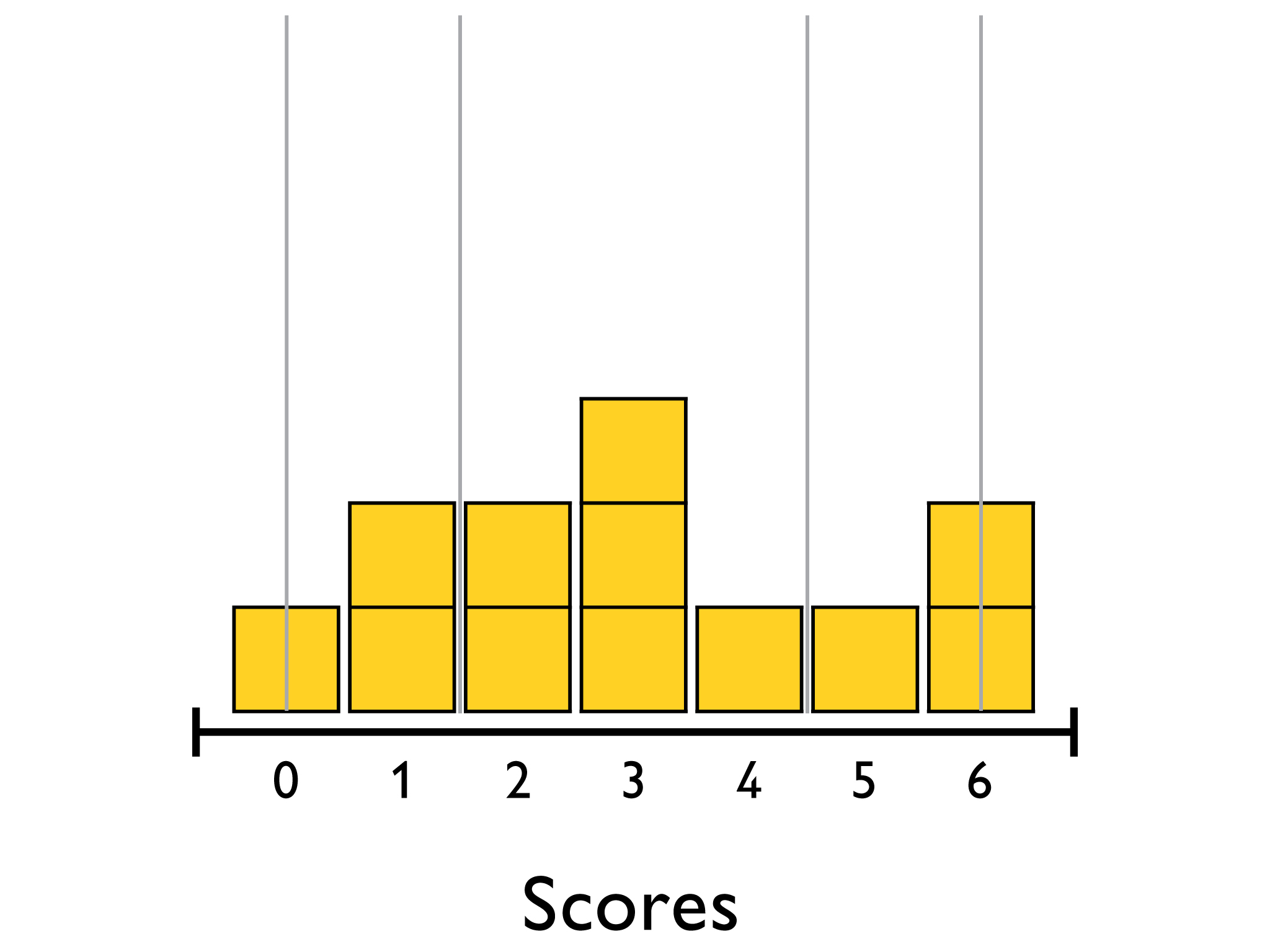
These are the quiz score data used in Lesson 4:
{0, 1, 1, 2, 2, 3, 3, 3, 4, 5, 6, 6}
Discuss how the five-number summary is represented in a box plot.
- The five-number summary for this data:
- Lower extreme: 0
- Lower quartile: 1.5 (because the middle pair of values for the lower half of the data is 1 and 2, and 1.5 is halfway between 1 and 2—{0,1,1,2,2,3})
- Median: 3 (because the two middle numbers are both 3)
- Upper quartile: 4.5 (because the middle pair of values for the upper half of the data is 4 and 5, and 4.5 is halfway between 4 and 5—{3,3,4,5,6,6})
- Upper extreme: 6
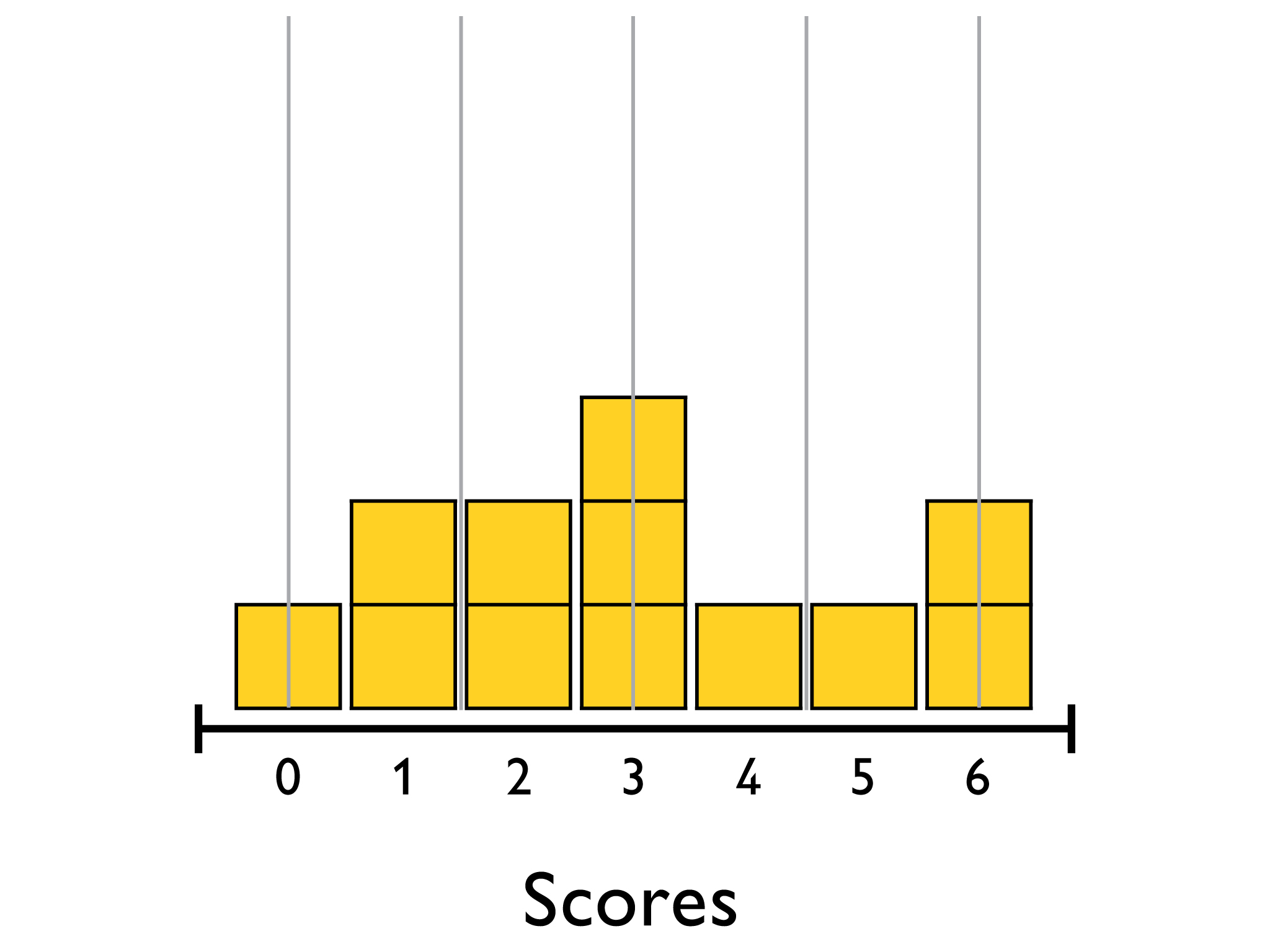
- Study the box plot below. Explain to a partner how the five-number summary was used to draw the box plot.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will construct a box plot to show the spread of their data about a sixth grade student.
Opening
Construct a box plot to show the spread of your data about a sixth grade student.
Create a Box Plot of My Data
Lesson Guide
Students will work individually as they calculate the five-number summary for their data and draw a box plot above their line plots from Lesson 7, Task 3. Students will need to have a copy of their line plot in their Notebook so they can draw their box plot directly above it. The copy can be a screen shot added to the Notebook, or the saved state of the interactive. If students are struggling to draw their box plots neatly, suggest that they add the Small Graph or Big Graph background option to their Notebook page.
Mathematics
Watch for students who are having difficulty finding the lower and upper quartiles, and notice whether there is an even or odd amount of data. Remind them that if there is an even number of values in the lower half of the data, the lower quartile is between the two middle values. If there is an even number of values in the upper half of the data, the upper quartile is between the two middle values.
When interpreting a box plot, students may mistakenly think that a long whisker or a long half of a box indicate that more values are represented by that part of the plot. Remind them that a box plot divides a data set into quarters and that each part of the plot represents the same number of data values. If one part of the plot is long, it indicates that the values in that quarter of the data are spread out. If it is short, it indicates that the values are bunched together.
To draw a box plot, draw vertical lines from the extreme values. These are the numbers that define the range and are called the lower extreme and the upper extreme. In the box plot they will visually show the range; the spread of the data.
Next, extend the lines showing the middle 50% of the data. These lines are called the lower quartile and the upper quartile.
Lastly, draw a line for the median.
Then draw horizontal lines to form a box around the lower to upper quartiles, and lines from the ends of the box to the extremes (the “whiskers”).
ELL: Help students access the mathematics by reviewing key information before beginning the problem. Walk students through the problem and make sure that the diagram shows all of the given information.
Interventions
Students have difficulty finding the five-number summary.
- Are your data listed in order?
- What are the least and greatest values? Write those down as the lower and upper extremes.
- Is there an odd number or even number of values?
- If there is an even number of values, how do you find the median?
- Once you find the median, write it down and focus only on the values below it. What is the middle of those values? This is the lower quartile.
- Now focus only on the values above the median. What is the middle of those values? This is the upper quartile.
Students have trouble drawing the box plot.
- Start with your line plot.
- For each value in your five-number summary, draw a vertical segment extending up from your number line.
- Use the segments to help you make the plot.
- First draw the box from the lower quartile to the upper quartile.
- Now draw the whiskers.
Students think a long box or a long whisker means there are more values in that part of the plot.
- To make your plot, you divided your data into four equal parts.
- What fraction of the data does the left whisker represent? The left half of the box? The right half of the box? The right whisker?
- Your data set has [number of values] values. How many values are in the left whisker? How many are in the right half of the box?
- If all the parts represent the same number of values, what would it mean if one part, say the right whisker, were very long?
- What would it mean if the left half of the box were very short?
Answers
- Answers will vary.
Work Time
Create a Box Plot of My Data
Find your work about a typical sixth grade student from the lesson "Describe a Sixth Grade Student". Copy your line plot from Lesson 7, Task 3, into your notebook.
- Find the five-number summary for your data.
- Draw the box plot directly above your line plot.
- On your box plot, label the lower and upper extremes, the lower and upper quartiles, the median, and the interquartile range (also called IQR).
INTERACTIVE: Line Plot with Stats
Hint:
Follow these steps to draw a box plot:
- Calculate the numbers in the five-number summary.
- Draw a box from the lower quartile to the upper quartile (this is the interquartile range, or IQR).
- Draw a line segment from the left side of the box to the lower extreme of the range, and a line segment from the right side of the box to the upper extreme of the range.
Prepare a Presentation
Lesson Guide
Students will prepare presentations to share with their classmates.
Preparing for Ways of Thinking
- Review the students' box plots.
- Select box plots that show different spreads of data to discuss in Ways of Thinking.
- Be sure to select at least one box plot for a data set with an outlier.
- Select both correct and incorrect box plots.
- Also select both thorough, accurate summaries and incomplete or inaccurate summaries.
ELL: When selecting a group of students to present in the Ways of Thinking section, ensure students present a topic they are confident about. Have students draw diagrams or demonstrate their knowledge in some other way than through verbal language alone.
Be sure to encourage ELLs to share, even if their pace might be slower than their native counterparts.
Challenge Problem
Answers
- The interquartile range has 16 values.
Work Time
Prepare a Presentation
- Give the five-number summary for your data.
- Show the lower and upper extremes, the lower and upper quartiles, the median, and the interquartile range.
- Explain what your box plot shows about the data.
- Show how the box plot relates to the line plot.
Challenge Problem
- If there are 32 data values in a set of data, how many values will be in the interquartile range?
Make Connections
Lesson Guide
Have students share their box plots.
SWD: Some students may need additional time to process prompting questions. Provide students with a written version of the question(s) so they can refer to them as a resource.
Mathematics
Discuss the box plots for data sets with outliers. Discuss how the outliers affect the shape of the box plot. If a data set has extreme outliers, you might ask students to ignore the outliers and redraw the plot. Discuss whether the new plot is a better representation of the shape of the data.
You might suggest that students draw and label a generic box plot to help them remember how the five-number summary is related to a box plot:
Consider these questions, emphasizing that a box plot shows measures of spread:
- Do the lower and upper quartiles need to be data values? (Answer: No, similar to the median they are the borders between quartiles.)
- What does a long whisker indicate? (Answer: It may indicate that there is an outlier or the data are spread out in that quarter.)
- Looking at the box plot, can you find any measures of center? (Answer: Only the median.)
- Looking at the box plot, can you tell the shape of the data? (Answer: No, not specifically because individual data points are not shown.)
- Looking at the box plot, can you tell how the data are spread? (Answer: Yes, this is the purpose of a box plot.)
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Prompt students to explain how they found the five-number summary, using precise language and correct statistical terms (lower extreme, upper extreme, median, lower quartile, and upper quartile.) Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Ask students to identify the errors and correct incorrect box plots.
Mathematical Practice 7: Look for and make use of structure.
- Ask students to describe what the structure of their box plots shows about the spread of the data. For example:
- A short box indicates a small interquartile range. This means the data are tightly clustered near the median.
- If the two halves of the box and the two whiskers are close to the same lengths, then the data are evenly distributed.
- A long whisker could indicate one or more outliers.
- If the box is close to either extreme, the data are skewed in that direction.
Performance Task
Ways of Thinking: Make Connections
- Take notes as your classmates present their box plots.
Hint:
As your classmates present, ask questions such as:
- How did you find the numbers in your five-number summary?
- How did you figure out where to draw the box?
- How did you find the interquartile range of your data?
- What does your box plot tell you about your data?
All About Box Plots
A Possible Summary
A box plot shows the five-number summary, which includes the lower extreme, the lower quartile, the median, the upper quartile, and the upper extreme. A box plot divides the data into four quarters (quartiles), with the box showing the middle 50% of the data. The width of the box is the interquartile range. A box plot does not show individual data or the shape of the data, but it does show how the data are spread.
Formative Assessment
Summary of the Math: All About Box Plots
Write a summary of what you learned about box plots.
Hint:
Check your summary.
- Do you describe a box plot and what it shows about a set of data?
- Do you describe each measure in the five-number summary?
- Do you describe the interquartile range?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to learn the ways in which students think line plots are similar to and different from box plots.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use these sentence starters below if you find them to be helpful.
Box plots are similar to line plots in the following ways …
Box plots are different from line plots in the following ways …