- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Review the Rubric
Self Check Exercise

Overview
Students analyze the data they have collected to answer their question for the unit project. They will also complete a short Self Check.
Students are given class time to work on their projects. Students should use the time to analyze their data, finding the different measures and/or graphing their data. If necessary, students may choose to use the time to collect data. Students also complete a short pre-assessment (Self Check problem).
Key Concepts
Students will look at all of the tools that they have to analyze data. These include:
- Graphic representations: line plots, box plots, and histograms
- Measures of center and spread: mean, median, mode, range, and the five-number summary
Students will use these tools to work on their project and to complete an assessment exercise.
Goals and Learning Objectives
- Complete the project, or progress far enough to complete it outside of class.
- Review measures of center and spread and the three types of graphs explored in the unit.
- Check knowledge of box plots and measures of center and spread.
Project Rubric
Lesson Guide
Have students look at the rubric and talk with a partner to describe it as completely as possible in their own words.
Tell students they will have today to analyze their data and prepare for the project presentations.
SWD: Students with disabilities may have a more challenging time identifying areas of improvement to target in their projects. Teach your students how to review a project using the rubric and a sample project.
ELL: If ELLs are still unsure about what a rubric is, show one and explain how it is used. Allow ELLs to use a dictionary if they wish.
Opening
Project Rubric
Work with a partner and review the project rubric.
- Take two minutes to study the rubric on your own.
- Then have one partner (without looking at the rubric) take one minute to describe the rubric as completely as possible to the other partner (who can see it). This partner should listen carefully to the description.
- Briefly look at the rubric again together. The partner who was previously the listener should now take 30 seconds to add to the description—without repeating any of it.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will analyze their project data in order to answer their statistical question.
Opening
Organize and analyze your project data in order to answer your statistical question.
Organize and Analyze Project Data
Lesson Guide
Students will work in their groups to make decisions about their project. Explain that they need to be clear about what is left to do on their project by the end of Work Time. Check with students as they work.
SWD: Students with disabilities may need review and reinforcement of the major skills and concepts covered in this unit. Make sure that students are in the best partnerships for their success and understanding.
Mathematics
Make sure students understand the measures of center (mean and median) and how to calculate them. These should be calculated even if they choose to analyze their data with a graph. The measures cannot be seen from the graphs, but students will have the data sets to calculate the measures.
As students work, ask them which type of graph (or graphs) would be most useful for their data sets and why.
Interventions
Students have difficulty getting started.
- Try making a line plot of your data to see what it looks like.
- What is the overall shape?
- Are there one or two values that appear more than others?
- Are there clusters or gaps?
- Are the data skewed to one side or another?
- Does the plot give you a sense of what might be typical about your data?
Students have trouble choosing the best measure of what is typical.
- Did you calculate the MAD for your data? How can the MAD help you figure out if the mean is typical?
- In your line plot, are the values close to the mean or are they spread out?
- Are there outliers that affect the mean? If so, consider the median. Does it seem typical?
- Are there one or two values that occur much more than others? Would the mode be a typical value?
Students choose an inappropriate plot or bin width.
Questions depend on a group's data set. Here are some examples:
- Your data have some big gaps, but I don't see this in your plot. What type of plot (or bin width) will show this feature?
- Your data have a value that is much greater than all the others. I don't see this in your plot. Is there a different type of display that will make this clear?
- Your data have two big clusters, but the other values are spread out. Is this clear in your plot? Is there a different type of plot that might show this better?
Answers
- Answers will vary.
- Answers will vary.
Work Time
Organize and Analyze Project Data
Organize and analyze the data you collected for your project. Consider these questions:
- What measures can you calculate to help you draw conclusions and to provide support for your conclusions? Examples: mean, median, mode, range, outliers, lower and upper extremes, lower and upper quartiles
- What graph(s) will best represent your data? Examples: line plot, box plot, histogram, or more than one graph
Hint:
Keep the rubric in mind as you work on your project.
Prepare a Presentation
Lesson Guide
Students will work with their groups to prepare their project presentations.
Preparing for Ways of Thinking
Highlight the Mathematical Practices during the Ways of Thinking discussion.
Mathematical Practices
This project provides an opportunity for students to engage in many of the Mathematical Practices.
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students must make sense of their statistical question and the data they have collected to help them answer it. They must determine the best way to organize the data and determine the measures that best summarize and describe what the data show.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Students must construct viable arguments to justify their conclusions based on the shape and distribution of the data and the statistical measures they have calculated.
Mathematical Practice 5: Use appropriate tools strategically.
- Students must choose the most appropriate measures and displays for their particular set of data. Students might also use spreadsheet and plotting tools to explore various data displays and help them choose the best one.
Mathematical Practice 6: Attend to precision.
- Students must communicate their conclusions and reasoning precisely in their project summaries.
Mathematical Practice 7: Look for and make use of structure.
- Students look for structure and patterns in their line plots and other data displays that can help them explain what the data show.
Challenge Problem
Answers
- Answers will vary.
- Answers will vary.
Work Time
Prepare a Presentation
Work on preparing your project presentation.
- Make sure your completed project presentation includes the following:
- Your data set
- At least one graph and an explanation of why the type of graph you used best represents your data
- Measure of center and/or spread
- A summary of what the graph and measures tell you about your data
- Your conclusion about what is typical for your set of data
Challenge Problem
- Suppose you had collected twice as much data. Do you think having twice the amount of data would change your conclusion, or reinforce it?
- Which of your measures would change? How would your graph(s) change?
Make Connections
Lesson Guide
Have students share their thoughts about the project and discuss possible additions to the rubric.
Mathematics
Consider these questions to elicit discussion about the rubric:
- What specific mathematical representations should we see used in the unit project?
- What should we consider an appropriate level of effort?
- How will we know if the conclusions are correct?
- What should we evaluate that is specific to a statistics unit?
Performance Task
Ways of Thinking: Make Connections
Look at the rubric again.
- Notice the blank column with the heading Specific to This Project. Is there anything that you think should be added to this column?
- Next look at the blank row at the bottom of the rubric. Is there any aspect of the statistics project that you think should be added here?
- Take a few minutes to discuss these questions with your partner. Write down any ideas you have.
- Be prepared to discuss your ideas as a class. As you propose an idea, make sure to say why you think it is important. After all ideas are discussed, the class will decide as a group whether to adopt any of the suggestions.
Measures of Center and Spread
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
SWD: Some students with disabilities may struggle with self-assessment; use your knowledge of student strengths and vulnerabilities to inform and create interventions you will put into place for this period of class time.
Interventions
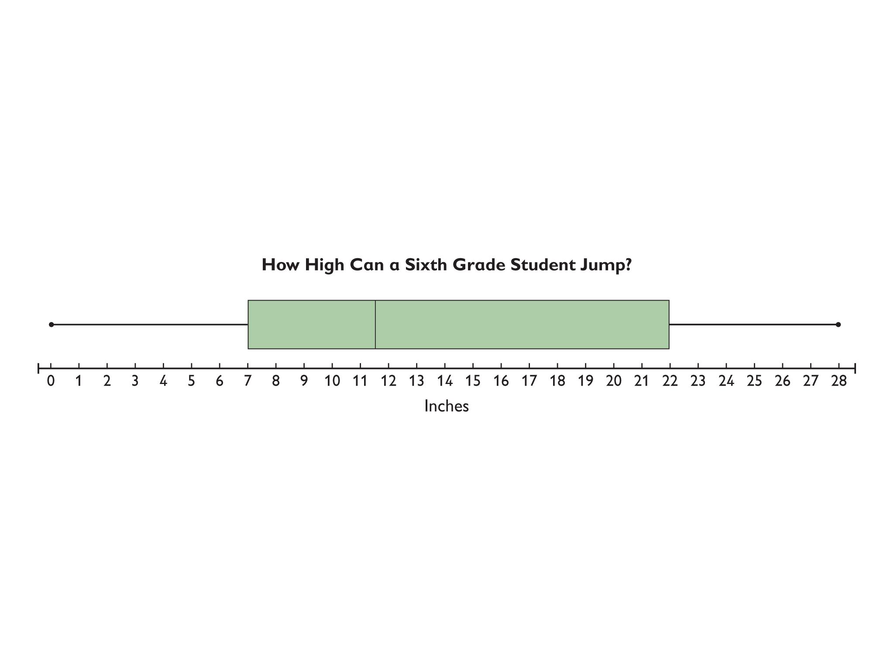
Student does not see that 0 and 28 must be data points.
- What is the range of the data?
- What are the extreme values?
- What do these two extreme values tell you about the data set?
Student does not see that the two data values around the median must add up to 23 (such as 11 and 12).
- What does the median represent?
- Is the number of data values even or odd?
- Since the median is 11.5, what does that tell you about the 2 data values on either side of it?
Student does not see that 7 and 22 must be data values.
- How many data values are in the first two quartiles and the second two quartiles?
- What is the median data value for the lower half?
- What is the median data value for the upper half?
Student does not connect the mean with the sum of the data.
- If the mean is 14 and there are 10 data values, what is the sum of the data values?
- What is the sum of the known data values?
- What do the rest of the data need to add up to?
Student provides a poor explanation.
- How can you convince a student in another class that your answer is correct?
Student provides adequate solution to all questions.
- Find a different way of solving the problem.
Answers
- Answers will vary.
- Answers will vary.
Formative Assessment
Measures of Center and Spread
Complete this Self Check by yourself.
This box plot shows a summary of a data set of 10 measurements, each measured to the nearest inch.
- Create a possible data set so that the mean of the data set is 15 inches.
- Show your work and explain how you created the data set.
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students' groups accomplished.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use these sentence starters below if you find them to be helpful. Share your reflections with your group.
Today my group accomplished …
Our next steps are …