Reviewing Data Sets

Overview
Gallery
Create a Data Set
Students will create data sets with a specified mean, median, range, and number of data values.
Bouncing Ball Experiment
How high does the class think a typical ball bounces (compared to its drop height) on its first bounce? Students will conduct an experiment to find out.
Adding New Data to a Data Set
Given a data set, students will explore how the mean changes as they add data values.
Bowling Scores
Students will create bowling score data sets that meet certain criteria with regard to measures of center.
Mean Number of Fillings
Ten people sit in a dentist's waiting room. The mean number of fillings they have in their teeth is 4, yet none of them actually have 4 fillings. Students will explain how this situation is possible.
Forestland
Students will examine and interpret box plots that show the percentage of forestland in 20 European countries.
What's My Data?
Students will create a data set that fits a given histogram and then adjust the data set to fit additional criteria.
What's My Data 2?
Students will create a data set that fits a given box plot and then adjust the data set to fit additional criteria.
Compare Graphs
Students will make a box plot and a histogram that are based on a given line plot and then compare the three graphs to decide which one best represents the data.
Random Numbers
What would a data set of randomly generated numbers look like when represented on a histogram? Students will find out!
No Telephone?
The U.S. Census Bureau provides state-by-state data about the number of households that do not have telephones. Students will examine two box plots that show census data from 1960 and 1990 and compare and analyze the data.
Who Is Taller?
Who is taller—the boys in the class or the girls in the class? Students will find out by separating the class height data gathered earlier into data for boys and data for girls.
Create a Data Set
Answers
- Answers will vary. Possible answer: Students with persistence and a basic understanding of mean and range may arrive at a correct solution through trial and error. However, the problems are easier if students use the mean as a point of balance as shown above.
- Possible answer:
- Answers will vary.
Work Time
Create a Data Set
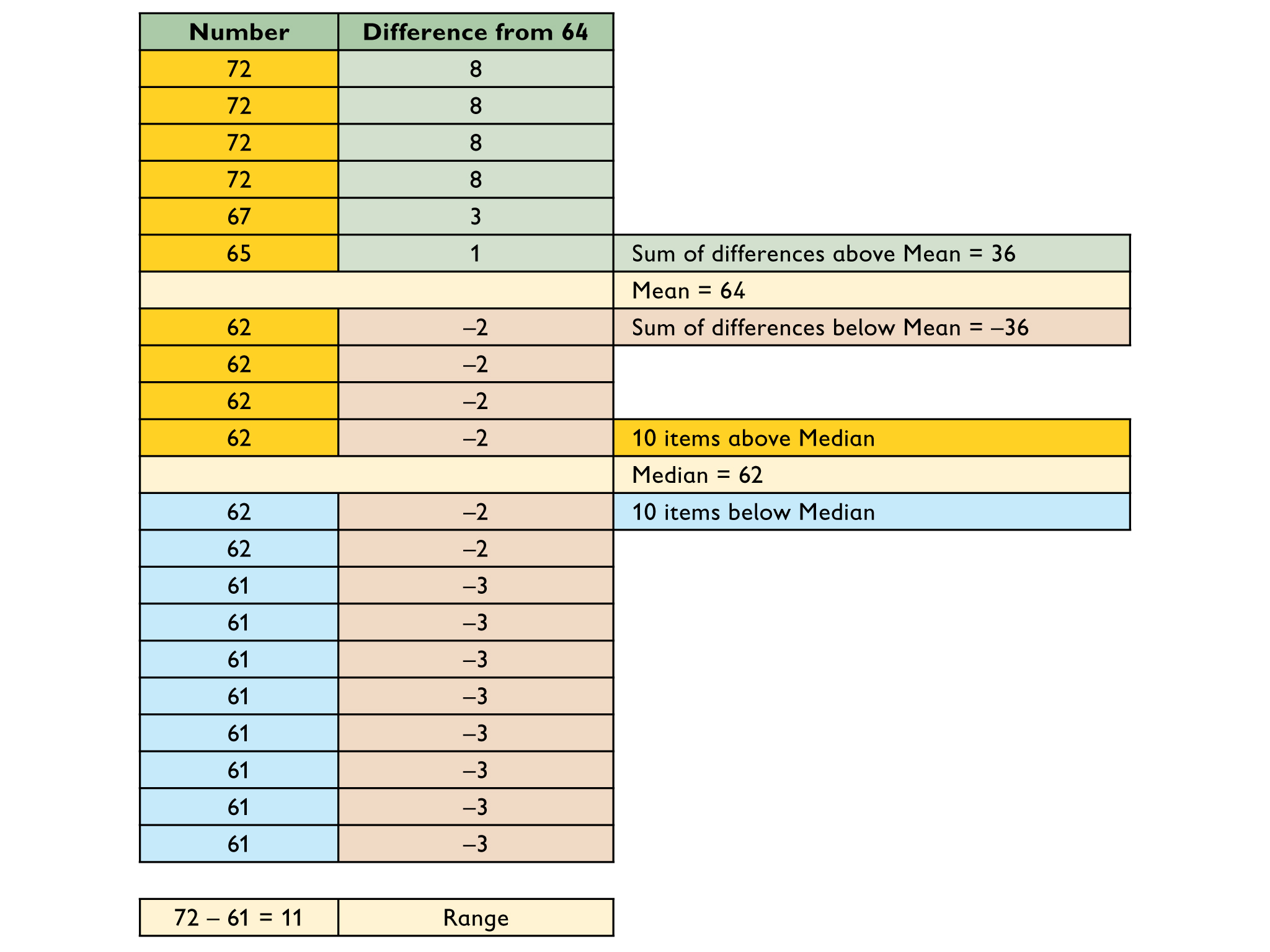
- Create a student height data set consisting of 20 values that meets the following criteria:
- The mean height is 64 inches.
- The median height is 62 inches.
- The range is 11 inches.
- List the set of data and show how it results in the given measures.
- Can you create another data set that results in the given criteria but does not include the data value of 64 inches?
Bouncing Ball Experiment
Answers
Materials: Ball and measuring tape
Part 1
- Student's predictions will vary.
- Students will record a list of measures.
- There will be a range of data, but it will likely be fairly narrow. Students will probably conclude that they don't need more data since their data will be fairly tightly clustered and the measures are likely to be close.
- Line plots will vary.
Part 2
- Measures of center will vary depending on the data collected.
- Answers will vary. Possible answer: The ball doesn't bounce in exactly the same spot every time it drops.
- The accuracy of student's predictions will vary.
- Students should use their line plot and measures of center to justify their conclusions.
- Answers will vary. Possible answer: All my data points are clustered around one value, so I don't think I need more data.
Work Time
Bouncing Ball Experiment
Part 1
In this unit you analyzed data to decide what is typical. Often your conclusion answered a question, such as “How tall is a sixth grade student?” In an experiment a question is also asked, but the question usually takes the form of “What will happen if ...,” rather than asking about the current status of something (height, for example). Experiments also often involve collecting data to answer the question. A hypothesis is the experimenter’s prediction about what he or she thinks the answer to the experimental question is.
Conduct an experiment to answer the following question: “How high will a ball bounce if it is dropped from a height of 3 feet?”
- Write your hypothesis about what will happen. Will the ball bounce half of its drop height? More? Less?
- Tape a yardstick or tape measure to a wall. Drop a ball from 3 feet and record how high it bounces in inches (or fractions of an inch).
- Repeat the experiment 20 times.
- Make a line plot for the data.
Part 2
Calculate the mean, median and range.
Why do you think there was a range of data?
Decide the answer to your question. Was your hypothesis correct?
Justify your conclusion using the line plot and measures as evidence.
Do you think you need more data? Why or why not?
Adding New Data to a Data Set
Answers
Part 1
- Mean = 2.5, median = 2.
- Answers will vary.
- The mean decreases.
- The mean decreases.
- The mean increases.
- The mean does not change; 2 is 0.5 below the mean and 3 is 0.5 above the mean, so the net effect on the mean is 0.
Part 2
- Answers will vary. The mean of the two numbers must be 2.5. Possible answer: 0 and 5
- Answers will vary. The mean of the three numbers must be 2.5. Possible answer: 1, 1, 5.5
- The mean increases to 5. This is not a good representation of the data. The median, which would be 2, is a better representation.
- Answers will vary. The mean of the two numbers cannot be 2.5 in order for the mean to change. One number must be less than or equal to 2 and one must be greater than or equal to 2 in order for the median to stay the same.
- Answers will vary. The mean of the two numbers must be 2.5 in order for the mean to stay the same. Either both numbers are less than 2 or both numbers are greater than 2 in order for the median to change.
Work Time
Adding New Data to a Data Set
Part 1
Use this data set to answer the questions that follow.
{ 1, 1, 2, 2, 2, 2, 3, 3, 4, 5 }
Determine the mean and median.
Identify a real-life situation that this data set could realistically represent.
What happens to the mean if a new number is added to the data set—for example:
What if 2 is added?
What if 0 is added?
What if 8 is added?
What happens to the mean if the numbers 2 and 3 are added to the given data set? Why does this result occur?
Part 2
- Find two numbers, that when added to the given data set, do not change the mean. How did you choose the two numbers?
- Find three numbers, that when added to the given data set, do not change the mean. How did you choose the three numbers?
- What happens to the mean if the number 30 is added to the given data set? How well does the mean represent the data set? Can you find another statistical measure that better represents the data set?
- Find two numbers, that when added to the given data set, change the mean but do not change the median. How did you choose the two numbers?
- Find two numbers, that when added to the given data set, change the median but do not change the mean. How did you choose the two numbers?
Bowling Scores
Answers
- Answers will vary. Possible answer: 135, 140, 145, 150, 160, 160, 160
- Mean: 150
- Median: 150
- Mode: 160
- Answers will vary. Possible answer: 140, 140, 140, 150, 175, 185, 190
- Mean: 160
- Median: 150
- Mode: 140
- Answers will vary. Possible answer: 135, 140, 145, 150, 175, 185, 190, 160
- Mean of the first seven scores: 160
- Mean of all eight scores: 160
Work Time
Bowling Scores
In this problem you will create bowling score data sets that meet different criteria. Note that bowling scores may be any whole number in the range 0–300 (most people score in the range 100–200). Create a new data set for each question.
- Create a data set of seven scores in which the data meet the following criteria: The mean and the median are the same but the mode is different.
- Mean of the set of scores
- Median of the set of scores
- Mode of the set of scores
- Create a data set of seven scores in which the data meet the following criteria: The mode is lower than the median but the mean is higher than the median.
- Mean of the set of scores
- Median of the set of scores
- Mode of the set of scores
- Create a data set of eight different scores (that is, none of the scores can be the same) in which the data meet the following criterion: When the eighth score is added to the set, it does not change the mean.
- Mean of the first seven scores
- Mean of all eight scores
Mean Number of Fillings
Answers
Answers will vary. Possible answer: Though mean is a measure of what is typical, it does not need to match any actual number in the group it typifies.
- The mean is a balancing act, so if no one has the mean, you must have some above and some below.
- Since 40 is the sum of all fillings, no one person could have more than 40.
- As many as 9 people could be filling-free if 1 person has all the fillings.
- Nobody has exactly the mean of 4 fillings. Could all 10 people have the next higher number of 5? No, because the total would be 50 fillings and the total must be 40. If 8 people had 5 fillings, the total would be 40. The other 2 must then each have 0 fillings. So, at least 2 people must have fewer than the mean.
- If 10 people with a total of 40 fillings each have the same number of fillings, that number can only be 4. We are told that no one has 4 fillings, so it is not possible that all 10 people have an equal number of fillings.
Work Time
Mean Number of Fillings
- Ten people sit in a dentist’s waiting room. The mean number of fillings they have in their mouths is 4. Yet none of the 10 people actually have 4 fillings. Explain how this situation is possible.
- These are all true statements. Explain why each one must be true.
- At least one person has more than 4 fillings and at least one has fewer than 4 fillings.
- No person has more than 40 fillings.
- From 0–9 people could have 0 fillings.
- At least 2 people must have fewer than the mean number of 4 fillings.
- It is not possible that all 10 people have an equal number of fillings.
Forestland
Answers
- Cannot be true. Possible justification: The segment from the upper quartile to the upper extreme covers 35%–76% forestland. This range accounts for only 5 of the 20 countries.
May be true. Possible justification: There is an even number of data points (20), so we find the median by dividing the sum of the middle two values by 2. If both middle values are 28%, the statement is true. But if not—say they are 30% and 26%—then no country has exactly 28% forestland.
May be true. Possible justification: The median is the middle value, 28. Could the 20 data points be distributed within the given box plot so that []
This requires that the sum of all percentages equals 560 [%]
Possible data set:
Here the sum of all percentages = 560 and the mean = 28.
Another possible data set:
Here the sum of all percentages = 550 and the mean = 27.5.
It is possible that the data set summarized by the box plot has a mean equal to its median, but it is not necessary.
- No. Possible explanation: The median percentage is still 28, but the lower values are now in a smaller range and the higher values are now in a wider range. The result is that the mean, though unknown, must be a percentage greater than 28. This is because there is no set of 20 values that fits the box plot while having a sum as low as 560. The lowest mean possible for this box plot is 29.25, because the lowest sum possible is 585:
Work Time
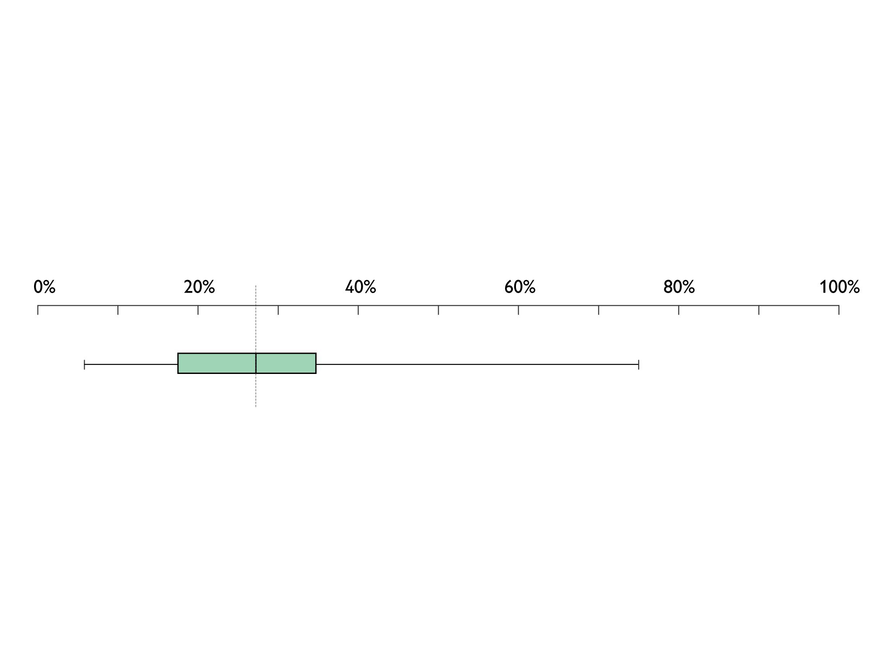
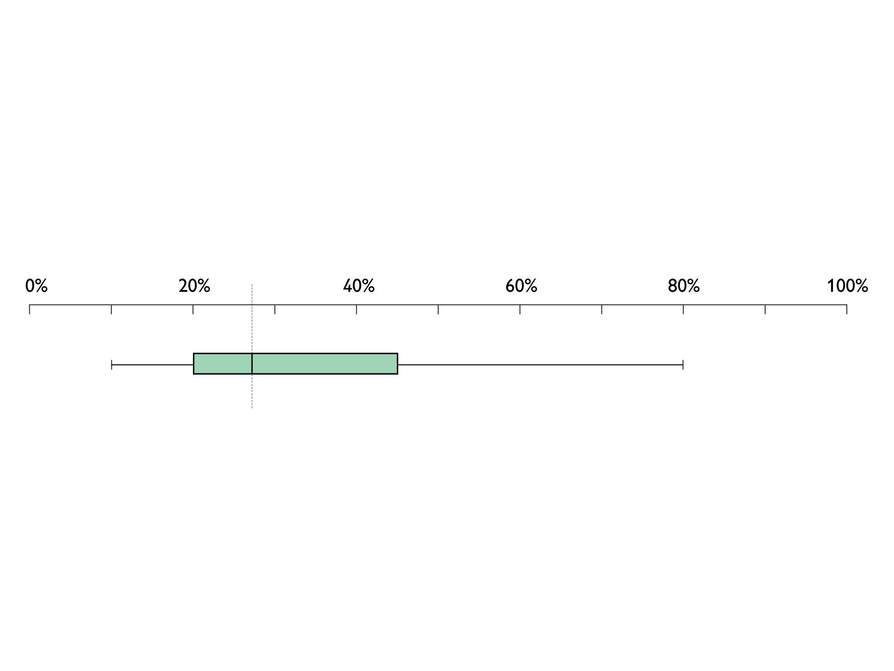
Forestland
The top box plot shows the percentage of the land in 20 European countries that is forestland.
- Read each statement below. Based on the top box plot, decide whether each statement must be true, may be true, or cannot be true. Then justify your answer mathematically.
- In most of the 20 countries, between 35% and 76% of the land is forestland.
- In at least one country, exactly 28% of the land is forestland.
- The mean of the data for these countries is 28%.
- If the box plot looked like the bottom one, could there be a data set for which the median and mean are both 28%? Explain why or why not this would be possible.
What's My Data?
Answers
- Answers will vary. Possible answer:
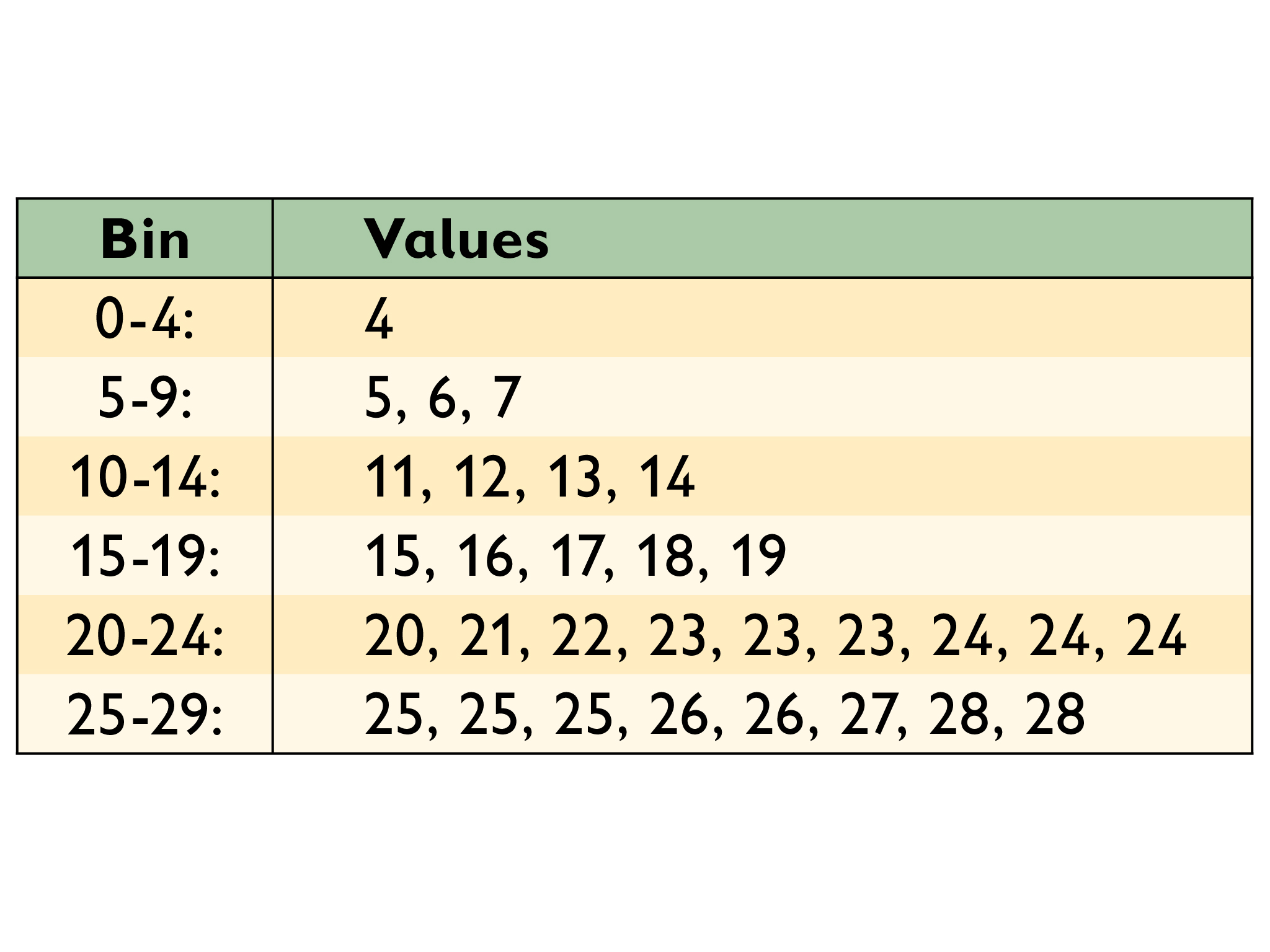
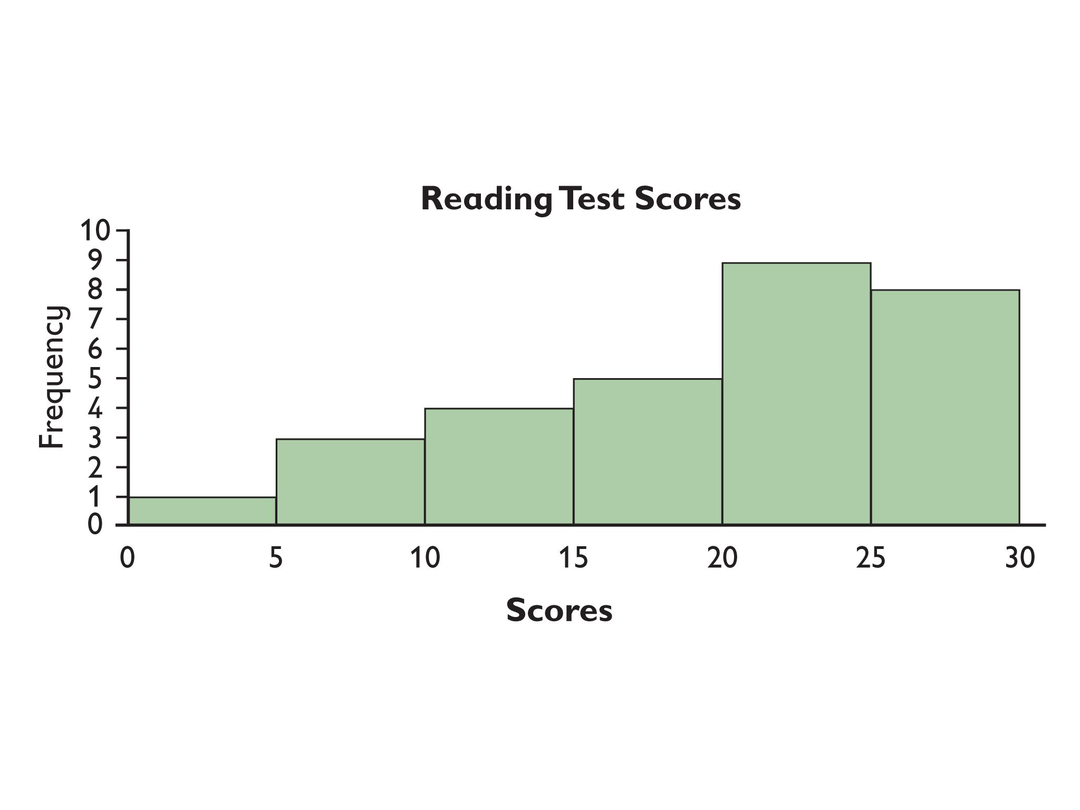
- There are 30 data points. The total can be determined by adding up the frequency of each of the bins.
- The median is in the bin from 20–24. There are 30 values, so the median is between the 15th and 16th values, which are both in the bin from 20–24.
To adjust for the farthest outlier, the data value in the first bin would be 0 and the lowest data value in the second bin would be 9. Possible data set: 0, 9, 9, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 28, 28
To have the narrowest range, the first bin should have the maximum data value (4) while the last bin has the least value possible (25). Possible data set: 4, 9, 9, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 23, 23, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25
To have the mode in the 15–19 bin, all five data values could be the same while all other values occur fewer than five times. Possible data set: 4, 7, 8, 9, 11, 12, 13, 14, 15, 15, 15, 15, 15, 20, 20, 21, 21, 22, 22, 23, 23, 24, 25, 25, 26, 27, 27, 28, 28, 29
Work Time
What's My Data?
- Create a data set for the histogram. Explain how you chose your data set.
- How many data points are there? Explain how you know.
- What bin is the median in? How do you know?
- Adjust your data set so that there is an outlier as far from the other data as possible.
- Adjust your data set so that the range is as narrow as possible.
- Adjust your data set so that the mode is in the 15 to 19 bin.
What's My Data 2?
Answers
- Lower extreme: 3
- Lower quartile: 9
- Median: 15
- Upper quartile: 18.5
- Upper extreme: 20
Answer will vary. Possible answer: The lower extreme, 3, must be a data point. The lower quartile, 9, indicates that there are either at least 2 scores equal to 9 or none. The median, 15, is a data value because there are an odd number of data points. The upper quartile, 18.5, indicates that there are either at least 2 scores equal to 18.5 or none. The upper extreme, 20, must be a data value.
The IQR is the difference between the lower and upper quartile: 18.5 − 9 = 9.5. This is the range that the middle 50% of the data are in.
Answers will vary. Possible answer: 3, 6, 9, 9, 9, 12, 15, 17, 18, 18, 19, 20, 20; 3, 15, and 20 are known values:
- 3, _, _, _, _, _, 15, _, _, _, _, _, 20 There are 6 data points in each half; 2 groups of 3 for each quartile. For the lower quartile, the numbers closest to it must add up to 18 (since it is 9). They could both be 9:
- 3, _, 9, 9, _, _, 15, _, _, _, _, _, 20 Similarly, the 2 values closest to the upper quartile must add up to 37 (18.5 x 2 = 37):
- 3, _, 9, 9, _, _, 15, _, _, 18, 19, _, 20 The remaining slots can be filled in:
- 3, 6, 9, 9, 9, 12, 15, 17, 18, 18, 19, 20, 20
Answers will vary. Possible answer: 3, 3, 3, 15, 15, 15, 15, 17, 17, 17, 20, 20, 20; Use the fact that the lower and upper quartiles and median do not have to be data points, but they are the mean of the middle pair of numerals. So, the middle pair of the lower quartile can be 3 and 15,
Answers will vary. Possible answer: 3, 9, 9, 9, 9, 9, 15, 18, 18, 18, 19, 19, 20; The data can be clustered around the lower and upper quartile by making the values as close to these numbers as possible.
Work Time
What's My Data 2?
This box and whisker plot represents the quiz scores of 13 students in Mr. Beel’s science class.
- Find the five number summary for the data shown in the box plot.
- Lower extreme
- Lower quartile
- Median
- Upper quartile
- Upper extreme
- What do these numbers tell you about the data?
- What is the interquartile range (IQR)? What does it tell you about the data?
- Create a set of 13 data values for the box plot. Explain how you chose your data set.
- Adjust your data set so that the values are clustered around the extreme values and the median.
- Adjust your data set so that the values are clustered around the lower and upper quartiles.
Compare Graphs
Answers
Answers for the histogram will vary.
Answers will vary. Possible answer: The histogram represents the data more clearly than the box plot. The IQR shows 50% of the data, but the data are not clustered in the box. The histogram shows the two clusters of data and gives an idea that there may be gaps.
Work Time
Compare Graphs
- Make a box plot and a histogram that represent the data in the line plot.
- Which of the three graphs represents the data best? Why do you think so?
Random Numbers
Answers
- Answers will vary.
- Answers will vary.
- Answers will vary. Possible answer: If the data are random, they should be roughly distributed among the 10 bins, with about 5 per bin. Students may argue that the data aren't random if they are evenly distributed since the numbers could be any number from 1 to 50. Any number is as likely as any other number, so the frequency of each number is equally likely, especially as the number of trials increases. Students have an opportunity to think about probability and how statistics is involved in understanding probability.
- Answers will vary.
- Answers will vary.
Work Time
Random Numbers
- Use a random number generator to generate 100 random numbers from 1 to 50, and then order the data. Random number generators can be found on the internet, in spreadsheet software, and on some calculators.
- Make a histogram with a bin width of 5 based on the data.
- What does your histogram look like? Do the data values appear to be random? Why or why not?
- Repeat steps 1 and 2, this time using 200 random numbers, and compare the results.
- Does using more data confirm or change your conclusion from question 3?
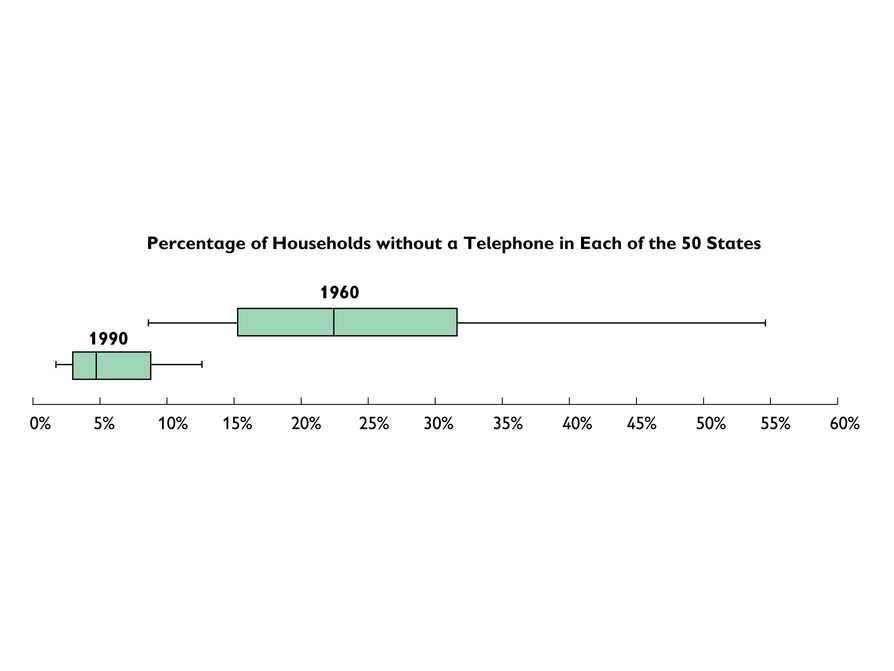
No Telephone?
Answers
- Answers will vary. Some points students might discuss in their analyses:
Large vs. Small Range
The range between the “phone-richest” and “phone-poorest” states in 1960 is about 46%, about 4 times as great as the range in 1990. In this situation, this means a great disparity among states; in 1960 there was at least one state in which fewer than half the households had phones and at least one state in which more than 90% of the households had phones.
Little Overlap of the Two Ranges
In fact, the ranges are so different, with so little overlap, that we can conclude that in most or all states, more households had phones in 1990 than in 1960. A percentage of household phones that would put a state in the top one-fourth of states in 1960 would put it in the bottom one-fourth in 1990.
Substantial Increase in Phone Ownership
For all 50 states, the median in 1960 is about 78% of households with phones. The median in 1990 is over 95% of households with phones.
Work Time
No Telephone?
For each one of the 50 states, the U.S. Census Bureau provides information about the percentage of households without a telephone. The percentage varies from state to state: In some states it is higher, while in others it is lower.
The box plot summarizes state telephone data for two different years—1960 and 1990.
- What do the box plots tell us about how telephone ownership in the 50 states changed from 1960 to 1990? Write an explanation. Provide as much specific information as you can.
Who Is Taller?
Answers
- Line plots will vary depending on the class data.
- Measures of center will vary depending on the class data.
- Answers will vary. Students should compare the measures of center for both data sets (girls and boys) and base their conclusion on those measures.
- Answers will vary. Possible answer: The line plots for boys and girls have different ranges than the line plot that has all the class data.
Work Time
Who is Taller?
To find out who is taller, the boys or the girls in your class, you need to separate the data set of student heights you collected in Lesson 2 into two data sets: one for boys and one for girls.
Make a line plot for each set of data. In order to compare the two plots, make the range and intervals of the horizontal line the same for both plots. Position one plot directly above the other.
Calculate the mean, median, mode, and range for each plot.
Decide which group of students is taller, and justify your answer using the measures you calculated.
How does each line plot compare to the class line plot for all of the students?