- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Sharing Apples 2
Construction of A Line Plot

Overview
In this lesson, students draw a line plot of a set of data and then find the mean of the data. This lesson also informally introduces the concepts of the median, or middle value, and the mode, or most common value. These terms will be formally defined in Lesson 6.
Using a sample set of data, students review construction of a line plot. The mean as fair share is introduced as well as the algorithm for mean. Using the sample set of data, students determine the mean and informally describe the set of data, looking at measures of center and the shape of the data. Students also determine the middle 50% of the data.
Key Concepts
- The mean is a measure of center and is one of the ways to determine what is typical for a set of data.
- The mean is often called the average. It is found by adding all values together and then dividing by the number of values.
- A line plot is a visual representation of the data. It can be used to find the mean by adjusting the data points to one value, such that the sum of the data does not change.
Goals and Learning Objectives
- Review construction of a line plot.
- Introduce the concept of the mean as a measure of center.
- Use the fair-share method and standard algorithm to find the mean.
Sharing Apples
Lesson Guide
Have students watch the video. Have students talk to a partner after watching the video. After discussing the mathematics, have pairs share their responses with the class. Then have students move on to the next task and watch the second video.
ELL: When showing the video, be sure that ELLs are following the explanations. Pause the video at key times, to allow ELLs time to process the information. Ask students if they need to watch it a second time. Ask questions to check for understanding.
Opening
Sharing Apples
Watch the video. It begins with students discussing how they could share their apples equally. As you watch, think about the mathematics that the students use.
- Talk to your partner about the method they used.
VIDEO: Sharing Apples
Introduction to the Mean
Lesson Guide
Have students watch the video. Have students talk to a partner after watching the video. After discussing the mathematics, have pairs share their responses with the class.
Mathematics
Have partners write an equation to show how the apples were shared.
(5 + 6 + 3 + 2 + 4) ÷ 5 = 20 ÷ 5 = 4
Explain to students that the video demonstrates an idea called the mean. The mean is calculated by adding all the values together and then dividing by the number of values. The mean is also sometimes called the average. We could say that although each of the 5 students started out with a different number of apples, the mean is 4 apples. Since the mean is a whole number, that means the apples can be shared equally between the students.
In the first video, the students move the apples around until they each have the same number. In the second video, the apples are added together (5 + 6 + 3 + 2 + 4 = 20) and then shared (or divided) evenly among the 5 students (20 ÷ 5 = 4), with each student getting 4 apples. This represents the standard algorithm for finding the mean.
In both examples, the sum of the apples is 20, and each of the 5 students gets 4 apples (4 × 5 = 20).
Explain that the mean is one measure used to describe a set of data.
Opening
Introduction to the Mean
Watch the second video to see how the students decided to share the apples. As you watch, think about the mathematics that the students use.
- Write an expression for the method they used.
For both methods, the students got the same number of apples. This number is the mean of the total number of apples.
The mean is a measure of center in a set of numerical data, computed by adding the values in a list and then dividing by the number of values in the list.
VIDEO: Sharing Apples 2
Math Mission
Lesson Guide
Discuss the Math Mission. Students will organize test scores in a line plot, and summarize them using the mean.
Opening
Organize quiz scores in a line plot, and summarize them using the mean.
Represent Math Quiz Data
Lesson Guide
Students can work individually to draw the line plot and answer the questions that are found in the following task. Remind them that a line plot is one way to visually display numerical data, and it can be used to describe the data.
SWD: As you confer with struggling students, try to move them toward efficiency. Scaffold their learning by starting with their strategy and another more efficient strategy. Help them to find the relationship between the two. Have students attempt the more efficient strategy the next time they need to find the mean.
Interventions
Student has difficulty making the line plot.
- First draw a number line.
- What will be the maximum and minimum values on your number line?
- What other values should you label?
- The first value listed is 6. How do you record this on the plot?
- The next value is 1. How do you record this?
- When you are done, how many Xs should you have over the number 1? How do you know?
Answers
Work Time
Represent Math Quiz Data
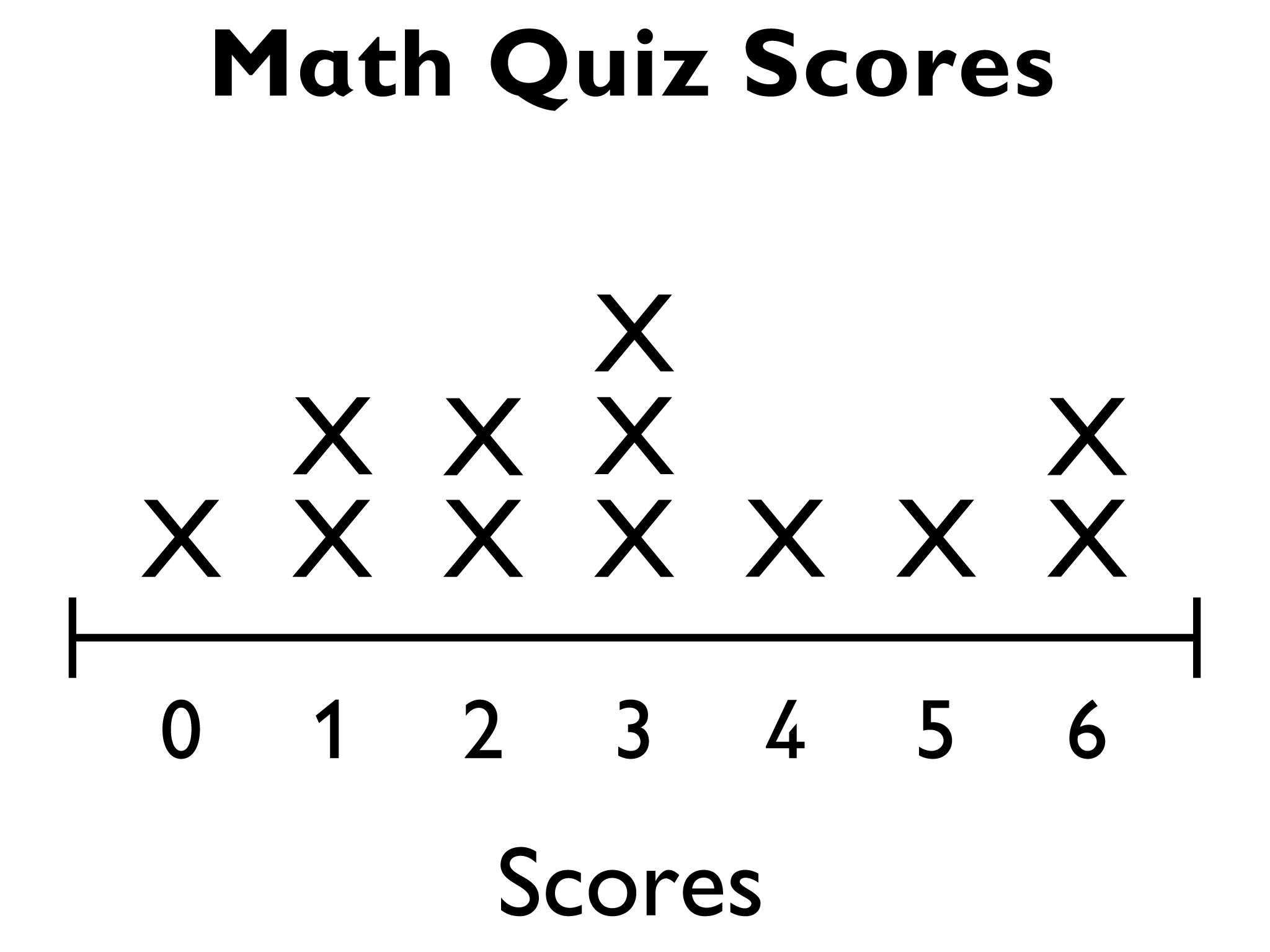
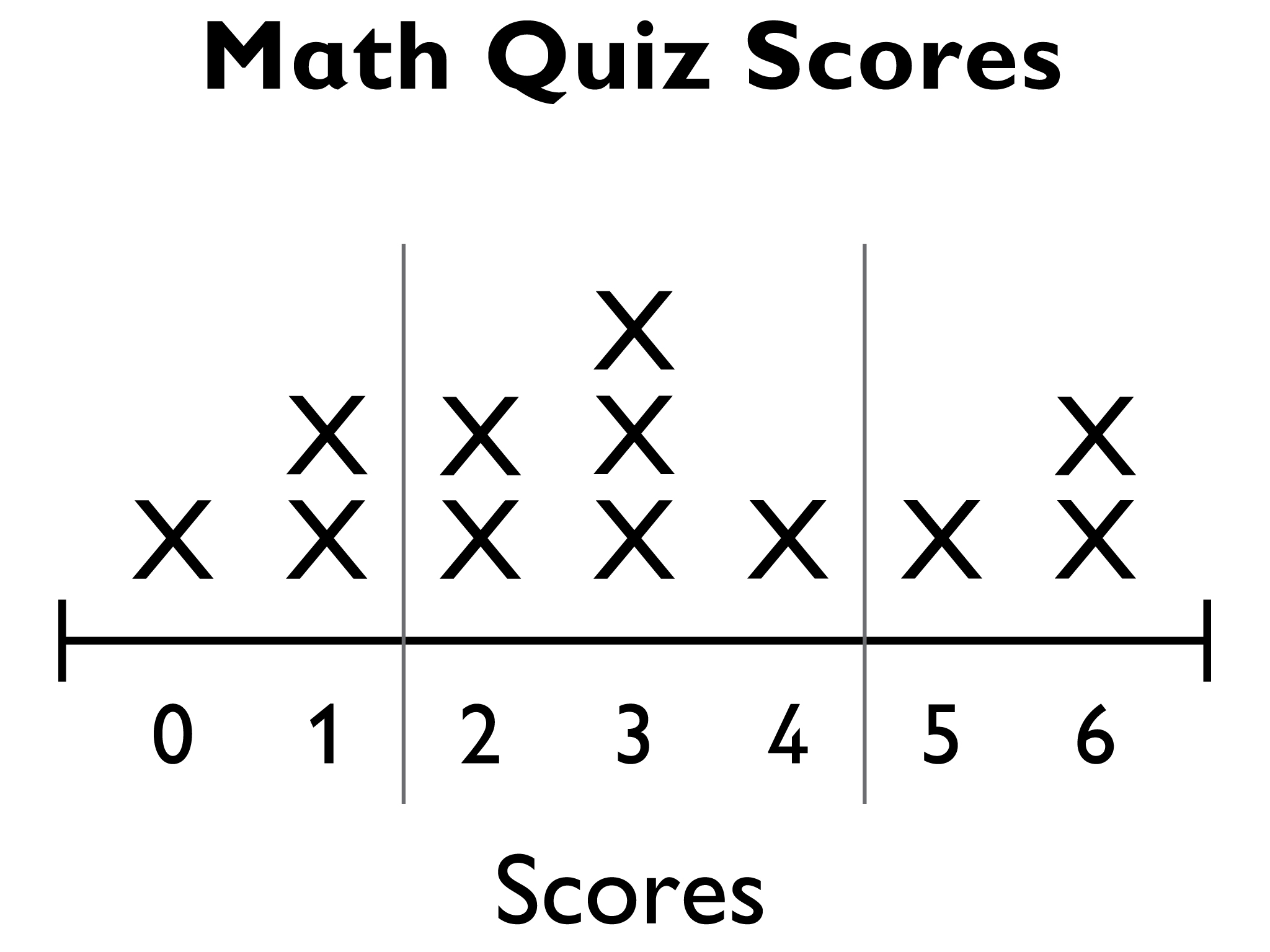
A class took a math quiz in which the highest possible score was 6 points. This data set shows the scores:
{6, 1, 0, 2, 3, 4, 3, 1, 2, 6, 3, 5}
- Sketch a line plot of the data.
Hint:
- Start by drawing a horizontal line.
- Find the extreme values in the data set. Write all of the possible numbers, from the minimum to the maximum, so that they are evenly spaced and under the line.
- For each value in the data set, place an X or a dot above the line in the appropriate column.
- Cross off each number in the data set as you go.
- Label the horizontal line and add a title to your line plot.
- Check that the number of Xs or dots in your line plot matches the number of values in the data set.
Analyze Math Quiz Data
Lesson Guide
Students will use the data from the math quiz to answer the questions.
Mathematics
The answers students find include the mode and the median, although those terms are not formally defined until the next lesson.
[common error] Watch for students who get the incorrect value for the middle score. Explain that to find the middle value, the data must be in order. Students can order the list of numbers or use the line plot. One strategy is to cross out the first and last values, then the second and next-to-last values, then the third and third-to-last values, and so on, until only the middle value or value pair is left.
Interventions
Student doesn’t remember how to find the mean of the data.
- Did you get the sum of the values in the data set?
- Did you count the number of values in the data set?
- Did you take the sum of the values in the data set and divide by the number of data values in the set?
Student has trouble finding the middle value.
- Did you list the values in order before finding the middle value?
- There are 12 values, so when the data are in order, where will the middle value be?
- The sixth value is 3 and the seventh value is 3. So, what is the middle value?
- In the line plot, the values are already in order. How can you find the median from the line plot?
Student has difficulty finding the middle 50% of the values.
- Did you list the values in order before finding the middle 50%?
- There are 12 values, so how many values is 50% of the values?
- These 6 values are in the middle 50%, so how many values are above and how many are below?
Answers
- The sum is 36.
- There are 12 data values.
- The mean is 3.
- Using the list of values or a line plot:
- The lowest score is 0. The highest score is 6.
- 3 occurs most often.
- 3 is in the middle of the data set.
- The middle of the values are the values from 2 through 4. These are the values between the vertical lines in the plot below.
- 3 is the typical score.
Work Time
Analyze Math Quiz Data
Using these same data about the math quiz, answer the following questions.
{6, 1, 0, 2, 3, 4, 3, 1, 2, 6, 3, 5}
- What is the sum of the values in the data set?
- How many data values are there?
- Find the mean of the data.
- Use either the list of values in the data set or your line plot to answer these questions:
- What is the lowest score? What is the highest score? The difference between the lowest score and highest score is called the range.
- Which score occurs most often? The score that occurs most often is called the mode.
- Which score is in the middle of the data? The middle value is called the median.
- Which score makes up the middle 50 percent of the data?
- What do you think the typical score is?
Hint:
To find the mean, add up all the data values and divide by the number of data values.
Prepare a Presentation
Lesson Guide
Students will prepare presentations to share with their classmates.
Preparing for Ways of Thinking
Look for the following:
- Students who use the fair-share method, rather than the add-and-divide method, to find the mean.
- Students who find the middle value and the middle 50% by using the list of scores, and students who find these values by using the line plot.
- Students who do not choose 3 as the typical score.
Ask these students to present their answers and reasoning during Ways of Thinking.
Challenge Problem
Answers
Answers will vary. Any two scores with a sum of 6 will not change the mean.
Work Time
Prepare a Presentation
Prepare a presentation that includes the following information:
- Explain how you found the mean.
- Explain how you identified the lowest score and the highest score.
- Explain how you identified which score occurs most often.
- Explain how you determined which score is in the middle of the data.
- Explain how you determined which scores make up the middle 50 percent of the data.
Challenge Problem
If two more students take the quiz, what could their scores be so that the mean does not change?
Make Connections
Lesson guide
Students will share their presentations.
SWD: Find two students that found the median using different strategies. Have both students present, then compare and contrast their solutions.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Have students share their methods for finding the median. Students might pair off the data values from either end of the range, use an ordered list of values, or use the line plot. Or, students might order the list and reason that, because there are 12 values, the middle value is between the sixth and seventh values on the list.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Discuss which method students find easier to understand and use.
Mathematics
Have selected students present their explanations. Choose students who can show different methods for determining the mean, median, mode, and range.
Students can find the sum of the data using just the data:
6 + 1 + 0 + 2 + 3 + 4 + 3 + 1 + 2 + 6 + 3 + 5 = 36
Or using the line plot:
There are 12 data values, so the mean is 3: 36 ÷ 12 = 3.
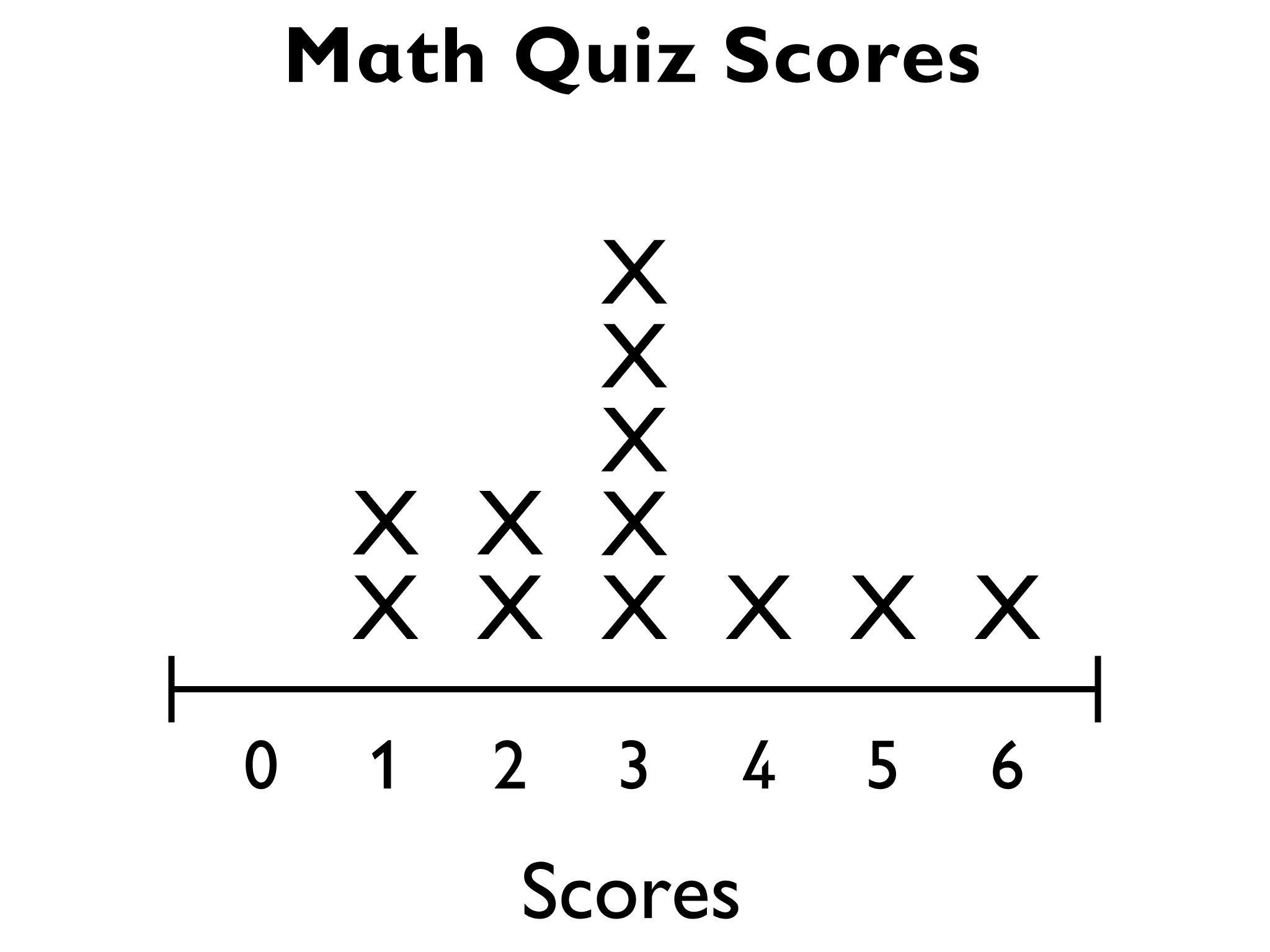
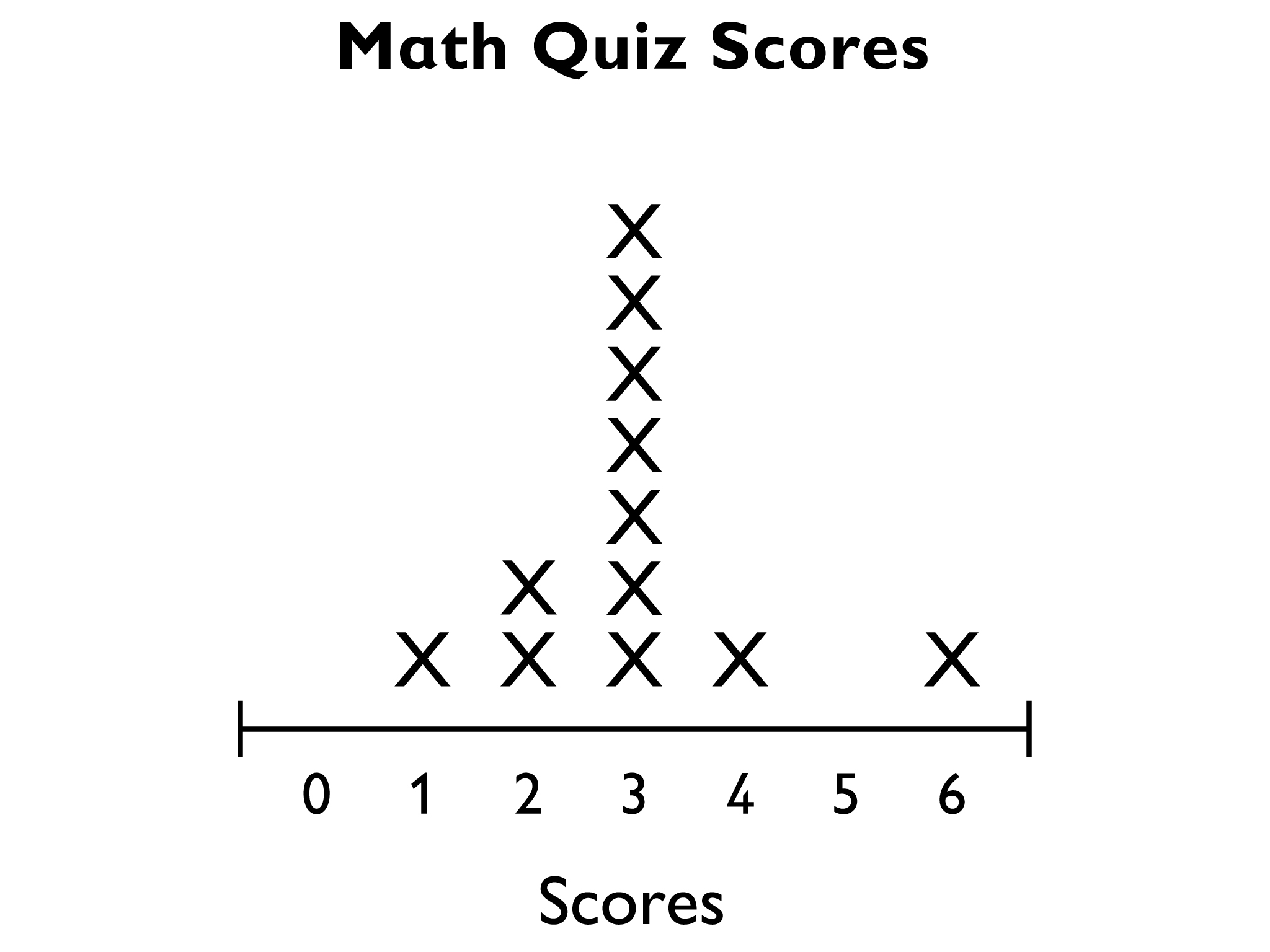
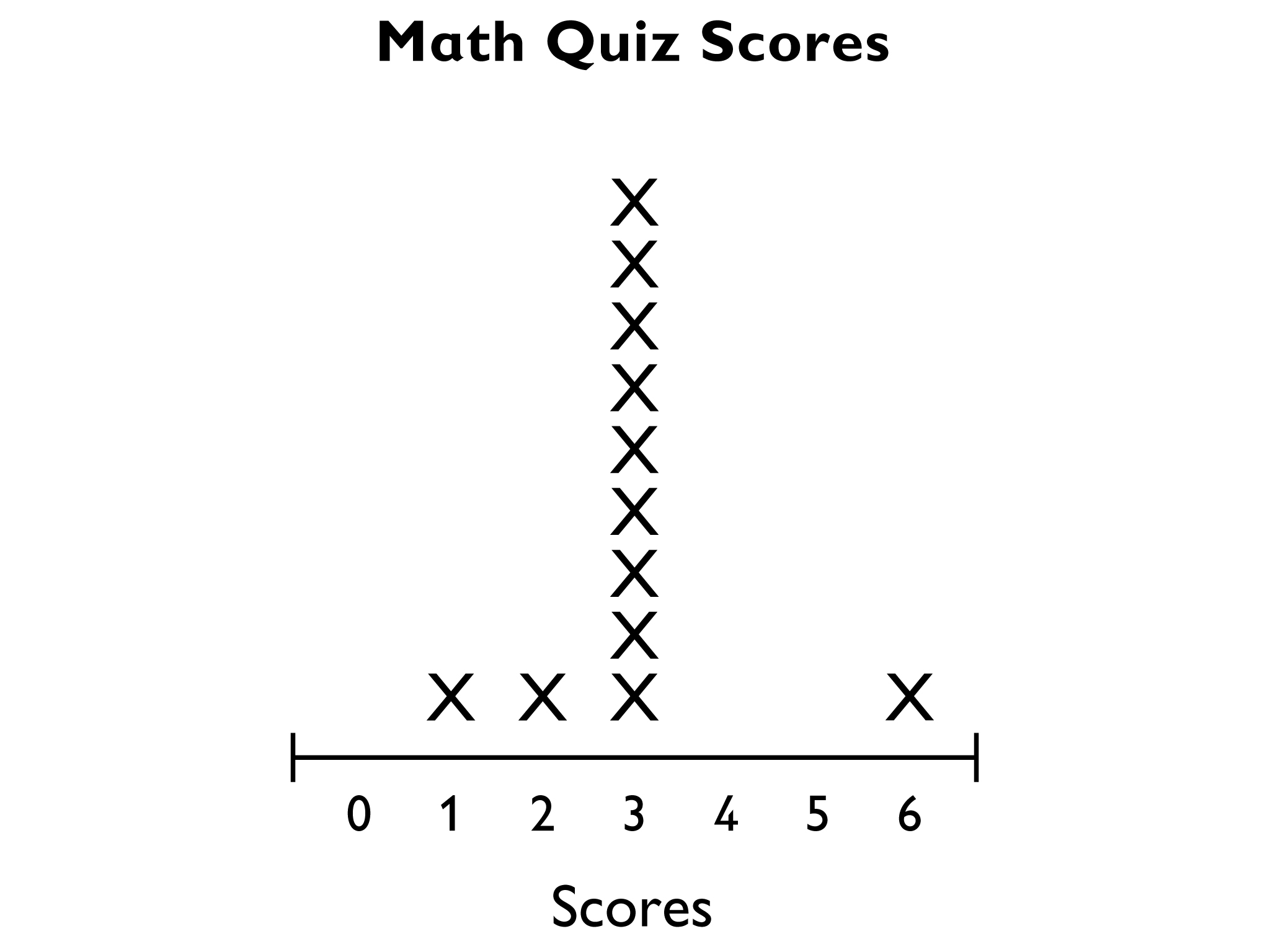
You can also use the fair-share method to look at the mean. Use the line plot to show what that might look like:
Starting with the line plot, the 0 score and one of the 6 scores can be moved to the 3 column because 0 + 6 = 3 + 3 (the 6 score “gives” 3 points to the 0 score).
Likewise, a 1 score and a 5 score can be moved to the 3 column (1 + 5 = 3 + 3).
A score of 2 and a score of 4 are moved to the 3 column:
Lastly, the 1 score, 2 score, and 6 score can be moved to the 3 column (1 + 2 + 6 = 3 + 3 + 3).
Notice that the total of the data is still 36 (3 × 12 = 36).
Be sure to mention in the discussion that sometimes you would have to do more adjusting to find the mean. Also, if the mean is not a whole number, adjusting with the line plot would not be a good method to use.
Discuss whether it is easier to find the set of scores with the most data using the list of numbers or using the line plot.
Discuss whether it is easier to find the middle score using the list of numbers or using the line plot.
Students can show the middle 50% of the data on the line plot. Since there are 12 data values, there should be 12 × 50% = 6 values in the middle 50%, 3 above the median, and 3 below. The middle 50% gives us an idea of where the data may be clustered.
As students present their work, ask questions like:
- Which method is easier?
- In what kinds of situations would one method be better than another?
- What do you think the typical score is? Why?
Performance Task
Ways of Thinking: Make Connections
Take notes as your classmates share how they calculated the mean and identified particular scores.
Hint:
As your classmates present, ask questions such as:
- How did you find the mean?
- How did you identify the lowest score?
- How did you identify the highest score?
- How did you identify which score occurs most often?
- How did you determine which score is in the middle of
the data? - How did you determine which scores make up the middle 50 percent of the data?
- How do the mean, the score in the middle of the data, and the score that appeared most often compare?
The Mean and Describing Data
Lesson Guide
Students read and discuss the Summary of the Math.
ELL: This discussion requires knowledge of the topic and knowledge of the academic language that corresponds to the topics. In order to support ELLs with their academic language and their language use in general, write the academic vocabulary on one side of the board (for reference).
- mean
- median
- mode
- range
- line plot
Formative Assessment
Summary of the Math: The Mean and Describing Data
Read and Discuss
- Mean: A measure of center in a set of numerical data, computed by adding the values in a list and then dividing by the number of values in the list.
- Median: A measure of center in a set of numerical data. The median of a list of values is the value appearing at the center of a sorted version of the list, or the mean of the two central values, if the list contains an even number of values.
- Mode: A measure of center that occurs the most often in a data set. There can be more than one mode, or none at all.
- Range: The difference between the least and greatest values in a data set.
Hint:
Can you:
- Describe what the mean is and how to calculate it?
- Describe what the median is and how to find it?
- Describe what the mode is and how to find it?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students learned about the mean.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use this sentence starter if you find it to be helpful.
One thing I learned about the mean is …