- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Box Plot
Manipulating Data Points

Overview
Students use the Box Plot interactive, which allows them to create line plots and see the corresponding box plots. They use this tool to create data sets with box plots that satisfy given criteria.
Students investigate how the box plot changes as the data points in the line plot are moved. Students can manipulate data points to change aspects of the box plot and to see how the line plot changes. Students create box plots that fit certain criteria.
Key Concepts
This lesson focuses on the connection between a data set and its box plot. It reinforces the idea that a box plot shows the spread of a data set, but not the individual data points.
Students will observe the following similarities and differences between line plots and box plots:
- Line plots allow us to see and count individual values, while box plots do not.
- Line plots allow us to find the mean and the mode of a set of data, while box plots do not.
- Box plots are useful for very large data sets, while line plots are not.
- Box plots give us a better picture of how the values in a data set are distributed than line plots do, and they allow us to see measures of spread easily.
Goals and Learning Objectives
- Experiment with different line plots to see the effect on the corresponding box plots.
- Create data sets with box plots that satisfy different criteria.
- Compare and contrast line plots and box plots.
Introduction to Making Box Plots With Line Plots
Lesson Guide
Have students study the box plot and line plot representing the data set to see how the plots are related. Ask students to think about how adding or removing points on the line plot might affect the box plot. Tell students that today they will be using an interactive to explore how the box plot changes as the line plot changes. Students can move, add, or remove any of the data points.
Mathematics
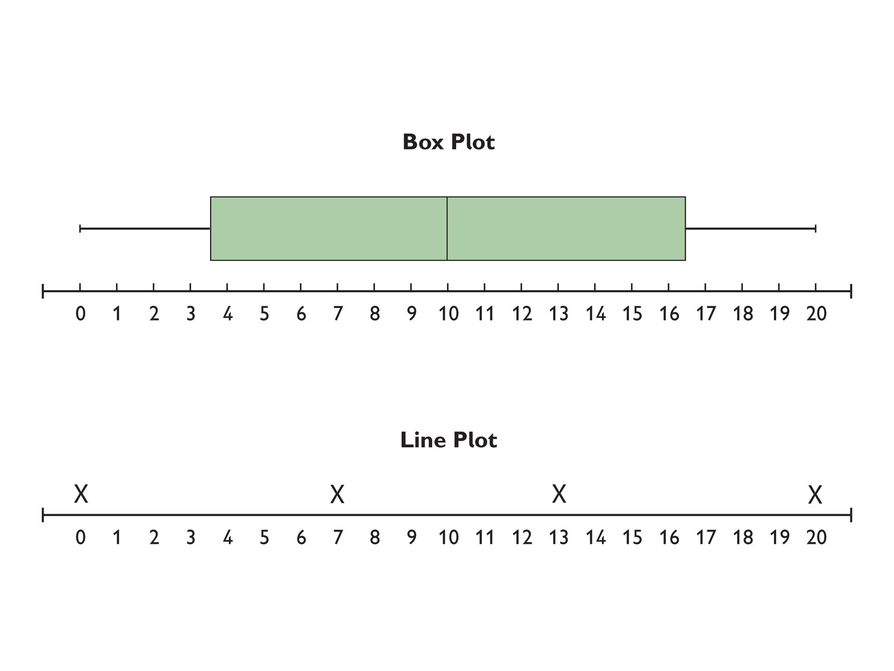
Elicit from students that since there are four data values, each must be one quartile, or one quarter of the data. The extreme values are 0 and 20. The median is halfway between 7 and 13, or 10. The lower quartile is halfway between 0 and 7, or 3.5. The upper quartile is halfway between 13 and 20, or 16.5.
- Any movement will change the box plot. For instance, if the data point at 13 is moved to 19, the left side of the box plot will not change, but the right side of the box (the upper quartile) will shift to 19.5 and the center of the box (the median) will shift to 13.
ELL: Ask students to tell you all of the new vocabulary terms for this lesson. Write the all terms on a chart, and have students volunteer to explain what the words mean. Encourage students to use pictures or diagrams, so that all students understand the explanations.
Opening
Introduction to Making Box Plots With Line Plots
This line plot and box plot represent the same data:
{0, 7, 13, 20}
- Why doesn't the size of the box on the box plot line up with the data underneath it on the line plot?
- What would happen to the "whiskers" if you changed the value of the lower or upper extreme values?
- How are the box plot and line plot related?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will create data sets with box plots that satisfy given criteria.
Opening
Create data sets with box plots that satisfy given criteria.
Explore Making Box Plots With Line Plots
Lesson Guide
Students will work individually as they spend a few minutes exploring the Box Plot interactive. After that, students will work in pairs. Make sure students save each of the box plots they create, so they can present them later.
SWD: Students with disabilities require review and reinforcement of mathematical tools and means of representing data. Reinforce how to interpret and utilize box plots.
Mathematics
The first five explorations demonstrate how the box plot can give us an idea of the shape of the data. The last three ask students to create a specific situation, so they need to focus on where the data needs to be to create that situation. They may notice that some movement (or addition) of data does not change the box plot.
Interventions
Students have difficulty connecting a description of a box plot to data values.
- Think about a data set with 12 values.
- How many values will be in each quarter of your data set?
- If the data are in order, what part of the plot shows the first three values? The next three? The next three? The final three?
- If the criteria tell you that a part of the plot is long, what do you know about the data in that part?
- If the criteria tell you that a part of the plot is short, what do you know about the data in that part?
- If the criteria tell you that the median is near one end of the box, what do you know about the data?
- What do you know if the box is symmetrical?
Students have difficulty creating a data set when they are given specific measures.
- Did you try starting with only a few points?
- Can you move the points around to get the value you want?
- What does the given information tell you about where the points need to be located?
- If you know the IQR, what are two possible values for the lower and upper quartiles?
- If you know the median, what fraction of your points needs to be above it? Does it matter what the specific values of these points are?
- What fraction of your points needs to be above the upper quartile?
Answers
- Answers will vary.
Work Time
Explore Making Box Plots With Line Plots
Explore making box plots when adding data to a line plot. Play with the data points and see what happens.
- Try to make a box plot for each of the following criteria:
- The box is very narrow and the whiskers are long
- The box is wide and the whiskers are short
- The median is to the far right or far left of the box
- One whisker is short and the other is long
- The box plot is symmetrical
- The interquartile range is 10
- The median is 6
- The upper quartile is 16
INTERACTIVE: Box Plot
Hint:
Think about a data set with 12 values.
- The box represents the middle 6 values. If the box is narrow, what do you know about these values?
- The left whisker represents the least 3 values. If the left whisker is long, what do you know about these values?
- The right whisker represents the greatest 3 values. If the left whisker is long, what do you know about these values?
- List 12 data values that you think will meet the criteria and use the Box Plot interactive to test them.
Prepare a Presentation
Lesson Guide
Students will prepare presentation to share with their classmates.
Preparing for Ways of Thinking
Review students' box plots. For each of the questions, select plots to share and discuss in Ways of Thinking.
Challenge Problem
Answers
- Answers will vary.
Work Time
Prepare a Presentation
- Explain why each box plot represents the given criteria.
- Describe the process you used to create box plots that meet the given criteria.
Challenge Problem
- Can you re-create any of the box plots you just constructed using different sets of data?
INTERACTIVE: Box Plot
Make Connections
Lesson Guide
Have student share the different box plots they made.
ELL: Create a written summary of the mathematics from the presentations. Some ELLs may benefit from this. In addition, this will serve as a resource when students are discussing and writing their own summary.
Mathematics
Ask students to describe the similarities and differences between line plots and box plots. For example:
- Both graphs use a number line, which shows each graph proportionally.
- The box plot does not show individual data, while the line plot does. This means that we cannot tell the number of data there are by looking at a box plot, while we can count the data points in a line plot.
- Both graphs can indicate the shape of the data to a degree.
- A line plot shows measures of center and a box plot shows measures of spread.
Consider these questions:
- What does the box plot show more clearly than the line plot? (Possible answers: the interquartile range, the median)
- What does the line plot show more clearly than the box plot? (Possible answers: the mode, outliers, individual data values)
- Which graph would be better for a data set of 1,000 values? (Possible answer: A line plot would be very difficult to read with 1,000 values, so a box plot would be more appropriate.)
- How does an outlier affect the box plot? (Possible answer: It lengthens a whisker.)
- How did you construct a different line plot that would give the same box plot? What does this tell you about box plots? (Possible answer: Adding the same number of data points in each quartile would keep the box plot the same. You cannot tell the size of a data set from the box plot. You cannot tell much about the shape of a data set from the box plot.)
SWD: When participating in a whole class discussion, Ways of Thinking can be intimidating for students with language based learning vulnerabilities and/or learning challenges. Have students work on the speaking and listening skills implicit to this portion of the lesson. Supports for students during this portion of the lesson include:
- In small groups or partners, give students a few minutes to discuss their ideas, the questions posed, and what has taken place during the lesson.
- Conference with individual students prior to the discussion to ascertain what they might be able to successfully contribute to the discussion. Students should rehearse their contribution and/or write notes for themselves to refer to when they speak. This will support students with expressive language difficulties and/or students who are anxious or reluctant to participate in class discussions.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Have students explain what they did to meet the criteria and defend their reasoning, using the terms: lower extreme, upper extreme, median, lower quartile, and upper quartile.
Mathematical Practice 6: Attend to precision.
- Students will attend to precision by using the correct vocabulary when describing their box plots.
Performance Task
Ways of Thinking: Make Connections
- Take notes as your classmates present their box plots.
Hint:
As your classmates present, ask questions such as:
- Can you explain how you created your box plot for that question?
- Which box plots did you have more difficulty creating?
- Which box plots were easier to create?
- What do you think it means when one whisker is short and the other is long?
About Box Plots
Lesson Guide
Have students discuss the summary with a partner before turning to a whole class discussion. Use this opportunity to correct or clarify misconceptions.
Formative Assessment
Summary of the Math: About Box Plots
Read and Discuss
- A box plot shows how data are spread. It does not show individual values like a line plot does. It is possible to create many different data sets with the same box plot.
- For example, once you make a box plot, you can add the same number of data points to each quartile and the plot will not change.
- You can see the median in a box plot, but you cannot tell what the other measures of center are like you can in a line plot.
Hint:
Can you:
- Discuss the characteristics of a box plot?
- Discuss the similarities and differences between the information a line plot shows and the information a box plot shows?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students can learn from looking at a box plot.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use this sentence starter below if you find it to be helpful.
When I look at a box plot, I can tell these things about the data …