Histograms As A Tool To Describe Data

Overview
Students make a histogram of their typical-student data and then write a summary of what the histogram shows.
Students are introduced to histograms, using the line plot to build them. They investigate how the bin width affects the shape of a histogram. Students understand that a histogram shows the shape of the data, but that measures of center or spread cannot be found from the graph.
Key Concepts
- A histogram groups data values into intervals and shows the frequency (the number of data values) for each interval as the height of a bar.
- Histograms are similar to line plots in that they show the shape and distribution of a data set. However, unlike a line plot, which shows frequencies of individual data values, histograms show frequencies of intervals of values.
- We cannot read individual data values from a histogram, and we can't identify any measures of center or spread.
- Histograms sometimes have an interval with the most data values, referred to as the mode interval.
- Histograms are most useful for large data sets, where plotting each individual data point is impractical.
- The shape of a histogram depends on the chosen width of the interval, called the bin width. Bin widths that are too large or too small can hide important features of the data.
Goals and Learning Objectives
- Learn about histograms as another tool to describe data.
- Show that histograms are used to show the shape of the data for a wider range of data.
- Compare a line plot and histogram for the same set of data.
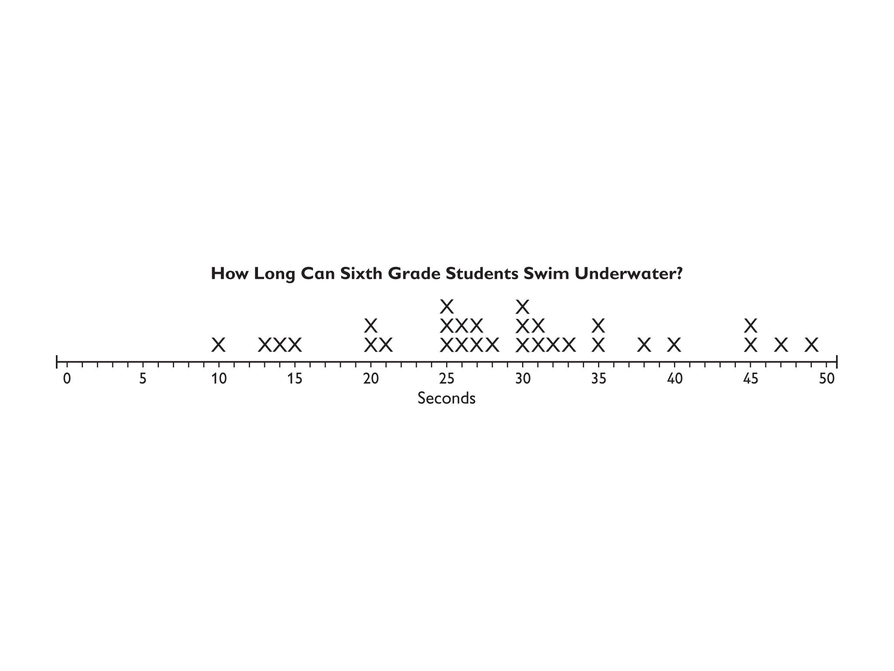
Sixth Graders Swimming Under Water
Lesson Guide
Have students look at the line plot and discuss the two questions with a partner.
Mathematics
Have students share their responses to the two questions. Bring out the following points in the discussion:
- The line plot is fairly flat.
- The data seem to be clustered toward the middle of the line plot, but it's difficult to see the shape of the data.
- There appear to be a few small clusters of data.
- If the data were grouped in some way it might be easier to see the shape of the data.
Have students suggest any ideas they have for different ways of showing the data.
Students have seen data grouped in intervals before, as quartiles in box plots. The widths of these intervals depend on the data and do not have to be the same size. Data could also be represented by using intervals of constant width.
Opening
Sixth Graders Swimming Under Water
Look at the line plot. It shows data collected in a sixth grade class about how long students can swim underwater.
Discuss the following questions with your partner:
- Can you easily see the shape of the data?
- What might you do in order to see the shape of the data better?
Make a Histogram
Lesson Guide
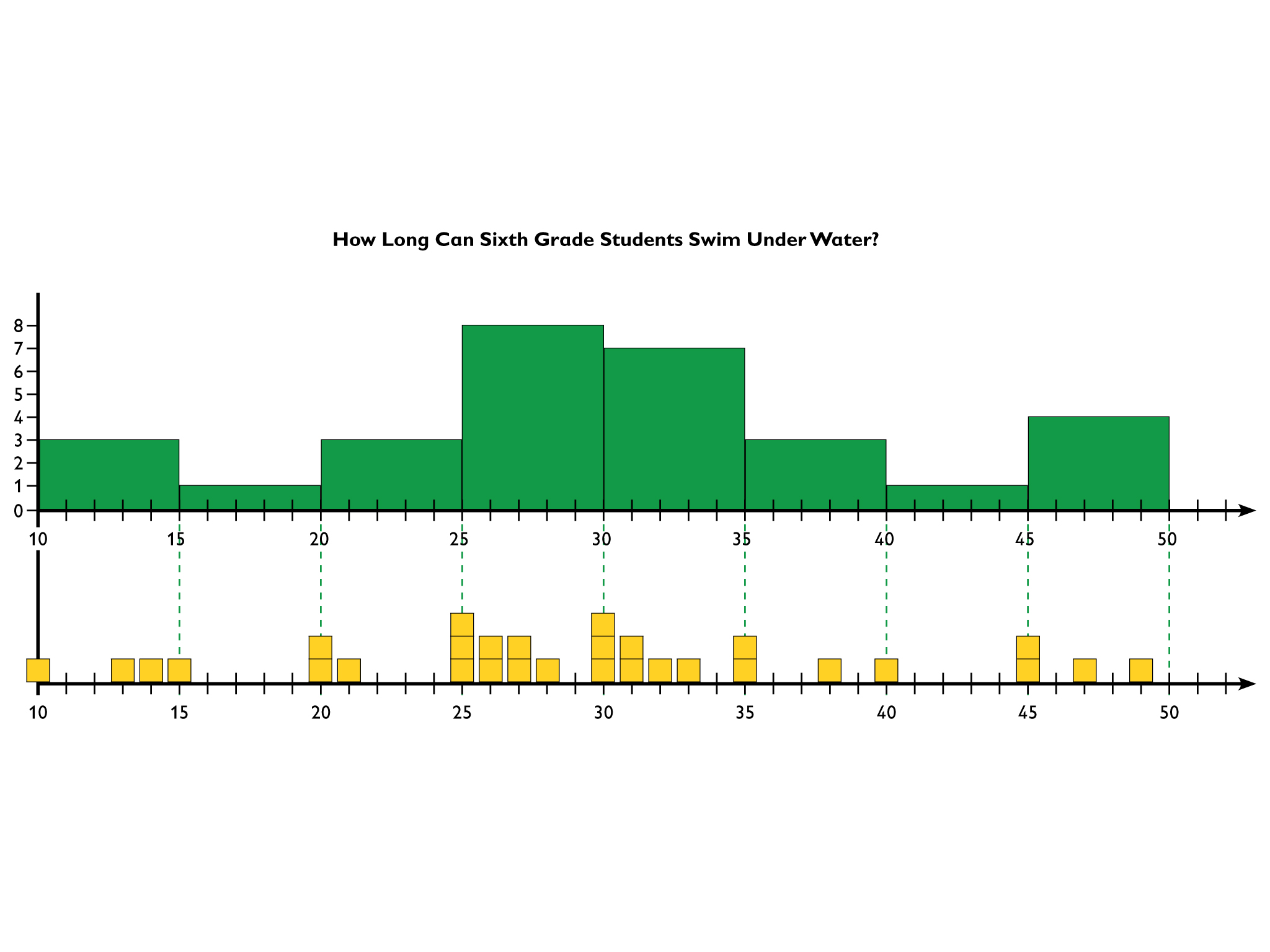
Once the idea of using intervals of constant width has been introduced, tell students that we can use a histogram for this set of data. Have the students follow along with you to draw the histogram on their tablet. Have students draw the histogram directly above the line plot so they can easily see how the two are connected.
ELL: Use adequate pace, and present the instructions in writing. Since students can see the tool while you are explaining, it might not be necessary to present the instructions in writing as long as the students follow you attentively. Monitor ELLs and check for understanding as appropriate.
Mathematics
In the line plot representation of this data set, observe that some of the data are clustered in 5-second widths. For this example, we will construct the histogram with a bin width, or range, of 5 seconds. The data within each range will be shown as a bar, called a bin.
Explain that a bin contains values from the left endpoint of the interval up to, but not including, the right endpoint. For example, in this histogram, the bin for the interval from 10 to 15 will include the values 10, 11, 12, 13, and 14, but not 15. The value 15 is included in the interval from 15 to 19.
Work with students to list the data values and find the frequency for each bin.
| Bin | Data Values in Bin | Frequency |
|---|---|---|
| 0–4 | None | 0 |
| 5–9 | None | 0 |
| 10–14 | 10, 13, 14 | 3 |
| 15–19 | 15 | 1 |
| 20–24 | 20, 20, 21 | 3 |
| 25–29 | 25, 25, 25, 26, 26, 27, 27, 28 | 8 |
| 30–34 | 30, 30, 30, 31, 31, 32, 33 | 7 |
| 35–39 | 35, 35, 38 | 3 |
| 40–44 | 40 | 1 |
| 45–49 | 45, 45, 47, 49 | 4 |
Begin constructing the histogram by drawing a frequency scale on the vertical line, directly above the line plot. Add vertical lines at 5-second intervals, the bin width. These lines will be the edges of the bins.
Outline and color each bin based on the frequency table. Finally, add a title and label the axes.
Ask students to discuss what the histogram shows. Is this a better visual representation of the data?
Opening
Make a Histogram
A histogram is a graph that shows data in intervals of equal size.
As a class, make a histogram for the data in the “How Long Can Sixth Grade Students Swim Under Water?” line plot. Use these steps:
- Decide on a range for each bin. This range is called the bin width, and it should be the same for each bin.
- Determine the number of data points in each bin.
- Draw a horizontal and vertical axis.
- Look at the highest number of data points in your bins, and use that number to determine your scale for the vertical axis.
- Divide the horizontal line into intervals based on your data and bin width.
- Label the vertical and horizontal lines and create a title for your histogram.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will make a histogram to show the distribution of data for sixth grade students.
Opening
Make a histogram to show the distribution of your data for sixth grade students.
Represent Data in a Histogram
Lesson Guide
Students will work individually as they draw a histogram using their data and line plot from Lesson 7. Some students may have such a narrow range in their data that they can't really draw a histogram. Those students can pair up with a student who has a more appropriate data set.
As students work, suggest that they think carefully about the bin width they choose. Using a bin that is very wide may group too many data values together and hide important patterns in the data. Using a bin that is very narrow can show too many individual values and make it difficult to get a sense of the overall shape of the data. Encourage students to experiment with different bin widths to see how the shape of the histogram changes.
[common error] Watch for students who are putting data values that are the endpoints of intervals in the wrong bin. Remind students that a bin contains data values for the left endpoint but not the right endpoint.
ELL: This lesson contains terms that may not be familiar. Point out to ELLs the corresponding parts of the histograms as you are explaining the components.
SWD: Students with disabilities may need direct instruction and/or guided practice to build efficiency and accuracy when creating bin widths. Provide direct instruction to those students who need added support.
Interventions
Students choose a bin width that is too wide.
- You will have only a few bars in your histogram. Do you think it will give a good picture of the data?
- Some of your intervals have a lot of data values. Did you consider making your intervals a little smaller?
Students choose a bin width that is too narrow.
- You will have a lot of bars in your histogram. Do you think that will give you a good picture of the data?
- Most of your intervals only have one or two values. Did you consider making your intervals a little larger?
Students incorrectly or inconsistently place data values that are in the endpoints of their intervals.
- [Point to an interval] Which values go in this interval? [Point to the next interval] Which values go in this interval? Check to make sure you placed your values correctly.
- If a value is on the border between two intervals, which interval should you put it in?
After determining the intervals and finding the values in each, students have difficulty constructing the histogram.
- Draw vertical lines to show the intervals for your bins.
- Draw a horizontal axis to show where the bottom of your bins will be.
- You will need a vertical axis to show the frequency, or the number of values in each bin.
- How many values do you have listed in the first bin?
- That number is the frequency, or height, of the first bin.
- Draw your first bin so its height is the frequency.
- Repeat this for all the other bins.
- What do you do if a bin doesn't have any values?
Answers
- Histograms will vary.
- Answers will vary.
- Answers will vary.
Work Time
Represent Data in a Histogram
- Make a histogram using the data you collected on your typical six grade student question.
- Decide what the range of each bin should be.
- Determine the number of data points in each bin.
- Create a frequency scale on the vertical line.
- Divide the horizontal line into intervals based on your bin width.
- Label the vertical and horizontal lines and create a title for your histogram.
- Write a summary of what your histogram shows about your data.
- How do you think your histogram would look if you used different intervals?
Hint:
- Each group of data in a histogram is called a bin . Each bin “fills up” with the data that belong in that bin. For example, in a histogram that represents height, each bin represents a range of heights.
- To make a histogram, you need to first decide the bin width. Each bin should be the same width.
- Remember that the bars in a histogram should touch each other.
Prepare a Presentation
Lesson Guide
Students will prepare presentations of their histograms.
Preparing for Ways of Thinking
Review the students' histograms. Select examples of the following to be shared and discussed during Ways of Thinking:
- Histograms that show different ranges of data and different choices for the bin widths. Be sure to select a histogram for a data set with a narrow range and a histogram for a data set with a wide range.
- Histograms with sensible bin widths and histograms with bins that are too wide or too narrow to give a good picture of the data.
- Histograms for data sets that have outliers.
- Histograms that have a clear mode interval.
Challenge Problem
Answers
- A histogram with a bin width of 1 would have a bar for each individual data value, with the height of each bar indicating the number of times that value occurs. This would be very similar to a line plot, except the height of the bar, rather than the number of dots, would indicate the frequency.
- A histogram with a bin width equal to the range would have one wide bar, with a height equal to the number of values in the data set.
Work Time
Prepare a Presentation
Discuss how you decided what bin width to use for your histogram and how you divided the horizontal line into intervals. Explain what your histogram tells you about a typical sixth grade student.
Challenge Problem
- What would a histogram with a bin width of 1 look like?
- What would a histogram with a bin width that is equal to the range look like?
Make Connections
Lesson Guide
Have students share the different histograms.
During the discussion, introduce the idea of a mode interval, the interval that contains the greatest number of data values. The mode interval will have the highest bin (the bin with the greatest frequency). Not every histogram has a mode interval.
Mathematics
For the data set with outliers, ask the presenter how the outliers are accounted for in the histogram. Do they “disappear,” ending up in an adjacent bin, or is there a gap (an empty bin) in the data as there is with the line plot?
Have students compare and contrast histograms and line plots:
- Line plots have a column of dots or Xs for each unique data value. Histograms group data values together into bins and use an axis to show the frequency for the entire bin.
- You can see individual values in a line plot, but not in a histogram.
- You can find the range, median, and mode from a line plot, but not from a histogram.
- You can find the number of values in a line plot by counting dots or Xs. In a histogram, you can find the number by adding the frequencies of the bins.
Consider these questions, emphasizing that a histogram shows the shape of the data:
- Did the distribution of data affect how you chose your bin width?
- How many data points are in the histogram? How do you know?
- Which graph (histogram or line plot) shows the shape of the data better? Why?
- Would your histogram look different with a different bin width?
- Looking at the histogram, can you tell what the range is or if there is an outlier? Can you tell what the mean, median, or mode is? Why?
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Ask presenters whether they think a histogram is a good representation of their data set and to explain why they think so.
- If the data set has a fairly narrow range, a line plot is probably the better representation. The students' histograms will demonstrate this as they will need to choose intervals of 2 or 3 that will probably make the shape of the data more like a block than the line plot.
- If the data set has a wide range, the histogram will show the shape of the data better.
After each presentation, ask the class to critique the histogram and tell whether they think the bin width gives a good sense of the data distribution, or whether it is too wide or too narrow.
Mathematical Practice 6: Attend to precision.
Encourage students to use precise language to explain how they chose their bin width and what the graph shows about the data.
Mathematical Practice 7: Look for and make use of structure.
For histograms with bin widths that are too wide or too narrow, work as a class to decide on a better bin width and reconstruct the graph.
Performance Task
Ways of Thinking: Make Connections
- Take notes as your classmates present their histograms.
Hint:
As your classmates present, ask questions such as:
- How did you decide what bin width to use for your histogram?
- What problems did you have in creating the histogram for your data about a sixth grade student? How did you deal with those problems?
- Can you explain what your histogram tells us about your data for a sixth grade student?
All About Histograms
Lesson Guide
Students have now been introduced to all of the concepts in this unit. If necessary, spend some time here reviewing concepts from earlier in the unit.
Formative Assessment
Summary of the Math: All About Histograms
Read and Discuss
- Unlike with line plots, measures of center and spread cannot be found by looking at a histogram, because individual data values are not shown. The number of data points in a histogram can be found by adding the frequencies of the bins.
- To make a histogram, you have to choose a bin width. You can choose a bin width based on where the data are distributed (so that the shape of the data is clear), or to organize the data in a logical way (such as by 10s or 5s).
Hint:
Can you:
- Explain what a histogram is?
- Make a histogram?
- Describe the type of data that a histogram is most useful for representing?
- Compare line plots and histograms?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what the most important thing students learned about histograms is.
SWD: The idea that three different presentations of data represent the same information may be challenging for students with disabilities. Review and reinforce this idea whenever possible to help students to comprehend and recall this importance concept.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use this sentence starter below if you find it to be helpful:
The most important thing I learned about histograms is ...