- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Line Plot with Stats
Understanding The Measure of Center

Overview
In this lesson, students are given criteria about measures of center, and they must create line plots for data that meet the criteria. Students also explore the effect on the median and the mean when values are added to a data set.
Students use a tool that shows a line plot where measures of center are shown. Students manipulate the graph and observe how the measures are affected. Students explore how well each measure describes the data and discover that the mean is affected more by extreme values than the mode or median. The mathematical definitions for measures of center and spread are formalized.
Key Concepts
Students use the Line Plot with Stats interactive to develop a greater understanding of the measures of center. Here are a few of the things students may discover:
- The mean and the median do not have to be data points.
- The mean is affected by extreme values, while the median is not.
- Adding values above the mean increases the mean. Adding values below the mean decreases the mean.
- You can add values above and below the mean without changing the mean, as long as those points are “balanced.”
- Adding values above the median may or may not increase the median. Adding values below the median may or may not decrease the median.
- Adding equal numbers of points above and below the median does not change the median.
- The measures of center can be related in any number of ways. For example, the mean can be greater than the median, the median can be greater than the mean, and the mode can be greater than or less than either of these measures.
Note: In other courses, students will learn that a set of data may have more than one mode. That will not be the case in this lesson.
Goals and Learning Objectives
- Explore how changing the data in a line plot affects the measures of center (mean, median).
- Understand that the mean is affected by outliers more than the median is.
- Create line plots that fit criteria for given measures of center.
Introduction to the Line Plot
Lesson Guide
Have the students look at the line plot. Ask them to think if there are other characteristics that describe the plot. Give students a few minutes to share their thoughts and then introduce the following terms:
- The mode is simply the number with the tallest column of dots (or the one that occurs the most frequently).
- The range is found by subtracting the least value in the plot from the greatest.
- The median is found by counting to the middle dot or by pairing dots on the ends until reaching the middle. The median may be halfway between two numbers, so it may be a decimal.
Also, note that there may not be a mode, if many numbers share the same highest frequency.
The median, mean, and mode are measures of the center, while range and MAD are measures of the spread.
Tell students that today in Work Time they will be exploring how the measures of center are affected as the line plot changes. Students will be able to add or remove any of the data points to a line plot and see the affect on the mean and median.
SWD: Some students with disabilities will benefit from a preview of the goals in each lesson. Students can highlight the critical features and/or concepts and will help them to pay close attention to salient information.
Opening
Introduction to the Line Plot
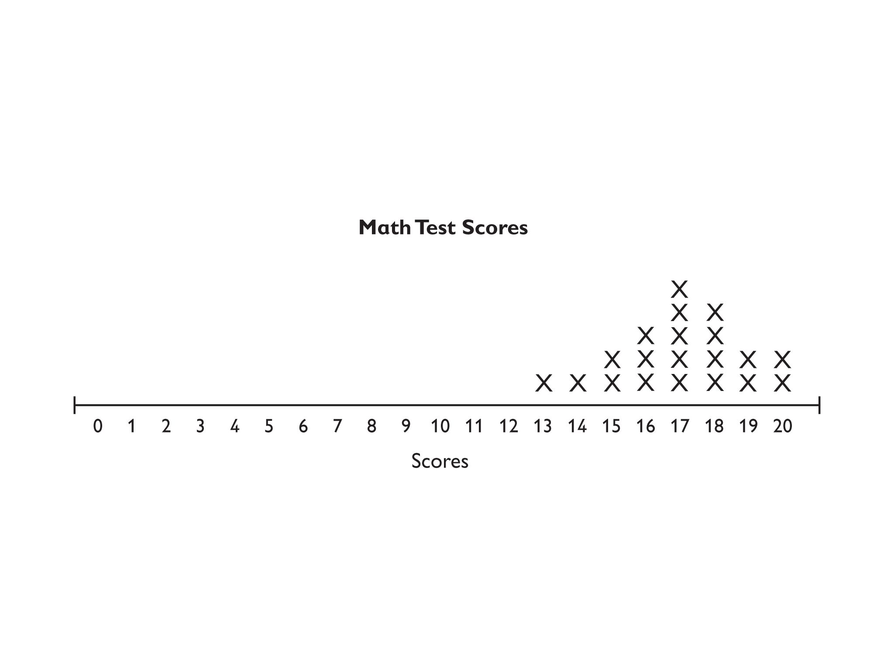
Look at this line plot.
- Without making any calculations, what do you think the mode, median, and mean are for the data shown?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will create line plots that fit given criteria about measures of center.
Opening
Create line plots that fit given criteria about measures of center.
Explore a Line Plot
Lesson Guide
Students will work individually as they spend a few minutes exploring the Line Plot with Stats interactive. They will learn how to add and remove data points. They will try to make line plots and see what happens to the mean and median as they change their data. (NOTE: Let students know that to change the starting number, they need to click and drag rather than use their finger.)
SWD: Students with disabilities may have difficulty learning how to utilize new and unfamiliar tools on the tablet. Make sure students have adequate instruction on how to use the tools as well as time for guided practice with the technology.
ELL: When listening to students' responses, give students advance notice they will be presenting their work on a specific problem during the Ways of Thinking section. This will give them ample time to prepare a thoughtful response.
Interventions
Student has difficulty using the interactive.
- How can you add points to the line plot?
- How can you delete points on the line plot?
- Where are the values for the mean, median and range? When do they change?
Student doesn't understand the connections between the line plot and measures of center.
- What happens when you add data points above the mean?
- How can you bring the mean up or down?
- What has to happen to lower the median?
- How do you calculate mean, median, range, and how would each be affected if you added more data?
Possible Answers
- In order to make a median greater than the mean, students will realize that the data must have a small range, with low values in the first half of the data. Here is an example of one such data set: {0, 0, 1, 2, 2, 3}. The median would be 1.5, whereas the mean would be about 1.3, giving a larger median than mean.
- In order for the median to not be one the data points, there needs to be an even number of data points where the middle two values are not the same value. They will need to be averaged to find the mean, giving a mean that is not one of the data points.
Work Time
Explore a Line Plot
Explore the line plot.
Start by entering some data. Explain what you did to reach each of the following goals.
- Make the median greater than the mean.
- Make a line plot in which the median is not one of the data points.
(NOTE: To change the starting number, you need to click and drag rather than use you finger.)
INTERACTIVE: Line Plot with Stats
Explore Measures of Center
Lesson Guide
Students will work in pairs to explore what happens to the measures of center when they change data points in their line plots.
ELL: When listening to students’ responses, give students advance notice they will be presenting their work on a specific problem during the Ways of Thinking section. This will give them ample time to prepare a thoughtful response.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- As students work with the interactive, they need to pay special attention to the values of mean and median as they change data points in their line plot. They must make explicit use of definitions of measures of central tendency to see how data at different values affects them and the line plot. Students’ success at these tasks demonstrates their ability to attend to precision.
Interventions
Students have trouble getting started.
- Start by experimenting.
- You know that the median is the middle value. Try making a plot with 7 values so the median is 5.
- How can you move the points so the median stays 5 and the mean becomes 5?
- Now try to move a point to make the mean greater. Why did the mean get bigger when you did this?
- Add one point above the median and one point below the median. Did the median change? Why does this make sense?
Students have difficulty determining how to add values without changing the mean.
- Start with a small data set, so it is easier to reason about the numbers.
- Remember that the mean is like a balance point for the data.
- Try adding a value 3 greater than the mean in your plot. Where can you place another point to make the original mean the balance point again? Test your idea.
Possible Answers
- If you add data above the mean, the mean will increase.
- If you add data below the mean, the mean will decrease.
- You can add data above and below the mean without changing the mean, as long as the total of the distances from the mean to the points above the mean equals the total of the distances from the mean to the points below the mean.
- Adding data above the median may increase the median.
- Adding data below the median may decrease the median.
- If you add the same number of data points above the median as below the median, the median will not change.
Work Time
Explore Measures of Center
With a partner, continue working with the line plot, and answer the following questions:
- What happens to the mean if you add data points above the mean?
- What happens if you add data points below the mean?
- Can you add data both above and below the mean so that the mean does not change?
- What happens to the median if you add data points above the median?
- What happens if you add data points below the median?
- Can you add data both below and above the median so that the median does not change?
- Think about whether the mean would go up or down if you added a data point above the mean.
- If the mean is 6 and you add a data point at 4, where would you have to add another data point so that the mean does not change?
INTERACTIVE: Line Plot with Stats
Hint:
Think about whether the median would go up or down if you added a data point above the median.
Prepare a Presentation
Lesson Guide
Students will prepare a presentation to share with classmates about how data can affect the mean and median.
Preparing for Ways of Thinking
Look for students who understand that adding data points above the mean will cause the mean to increase, adding data points below the mean will cause the mean to decrease, and sometimes adding data points above and below the mean will have no change to the mean.
Challenge Problem
Possible Answer
- Yes, it's possible for the mode to be greater than the median when the mean is less than the median. Example: 4, 4, 3, 6, 1, 2 In the set above, the median is 3.5, the mode is 4, the mean is about 3.3.
Make note of students that understand that you can have a median that is not a data point, and understand how you could have a data set where the mean, median and mode are all the same value.
Listen for students that think the median is affected by adding or removing data points in the same way that the mean is affected by adding or removing data points, and address these misconceptions during the Ways of Thinking discussion.
Interventions
Students struggle with the Challenge Problem.
- Start by deciding where your median will be. Put an equal number of points above and below it.
- Move the points around, but keep them on their side of the median. How does the median change?
- Next decide where the mode will be and move the points appropriately.
- Finally, how can you move points to get a mode that is greater than the mean and the median?
Work Time
Prepare a Presentation
Prepare a presentation that explains how you changed the measures of center by adjusting the points on the line plot.
Challenge Problem
- Is it possible for the mode to be greater than the median when the mean is less than the median?
Make Connections
Lesson Guide
Have students share the different line plots and any interesting observations or discoveries they made while creating line plots.
ELL: In facilitating the discussion, provide appropriate pace and ample wait-time to allow for thoughtful participation by ELLs. Present key words in writing, and allow students to use dictionaries before responding. Additionally, if the language proficiency of at least a few students is low, present some sentence frames to help them with the structure of the sentences. You can use the sentences provided here to create the sentence frames “When creating my line plots … I discovered that mean, median, range, and outliers relates the measures of center because …”
Mathematics
Questions for discussion:
- How did you go about separating the median and mean?
- Which measure do you think best represents the data when there is a wide range? (Answer: The median is probably a better measure, because the mean would reflect extreme values and any outliers.)
- When will the median not be a point in the data set? When will it not be a whole number? (Answer: If there is an even number of data points, the median is between the two middle values. If the two middle values are different, then the median will be halfway between those values, and it will not be a value in the data set. If one of the middle values is even and one is odd, then the median will not be a whole number.)
- What happens when you have an outlier? Which measure is affected the most? (Answer: The mean is affected the most, but the range and the MAD are also affected.)
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Require students to explain what they did to meet the criteria, using precise language, including the terms: mean, median, mode, range, and outlier.
Mathematical Practice 7: Look for and make use of structure.
- Have students comment on the structure of their plots and how the structure relates to the measures of center.
Performance Task
Ways of Thinking: Make Connections
- Take notes about any interesting discoveries that your classmates made about how adding or removing data points from a line plot affects the measures of center.
Hint:
As your classmates present, ask questions such as:
- What was your goal when you explored the Line Plot with Stats interactive? How did you reach that goal?
- What determines whether the mean will change and how it will change when you add data to a data set?
- What determines whether the median will change and how it will change when you add data to a data set?
Mean, Median, and Mode
Lesson Guide
Have students review what they learned in this lesson. Be sure the students understand the points below:
- A set of data can be visually represented with a line plot.
- The data can be described using measures of center (mean, median, mode) and measures of spread (range, mean absolute deviation).
- If data have a wide range or if there are outliers, the median is a better descriptor of the data set than the mean because it is less affected.
- The measures of center and the range give us a good idea of the shape of the data.
- The mean and median do not have to be data values, but the mode (if it exists) is always a data value.
Formative Assessment
Summary of the Math: Mean, Median, and Mode
Read and Discuss
- Measures of Center
- Mean: A measure of center in a set of numerical data, computed by adding the values in a list and then dividing by the number of values in the list.
- Median: A measure of center in a set of numerical data. The median of a list of values is the value appearing at the center of a sorted version of the list—or the mean of the two central values, if the list contains an even number of values.
- Mode: A measure of center that occurs the most often in a data set.
- Measures of Spread
- Range: The difference between the extreme (least and greatest) values in a data set.
- Mean Absolute Deviation: A measure of variation in a set of numerical data, computed by adding the distances between each data value and the mean, then dividing by the number of data values.
- Outlier: A data value that is far from the rest of the data.
Hint:
Can you:
- Explain how the different measures of center are affected when data values are added or moved?
- Understand why the median and mean of a data set do not have to be data values, but why the mode, if it exists, will always be a data value?
- Describe or give an example of a data set for which the median is a better measure of what is typical than the mean?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what connections students see between a line plot and measures of center and spread.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use this sentence starter if you find it to be helpful.
When I look at a line plot, this is how I find or estimate the measures of center (mean, median, and mode) and spread (range and outlier) ...