Algebraic Expressions & Equations

Overview
Students use algebraic expressions and equations to represent rules of thumb involving measurement. They use properties of operations and the relationships between fractions, decimals, and percents to write equivalent expressions.
Key Concepts
Expressions and equations are different. An expression is a number, a variable, or a combination of numbers and variables. Some examples of expressions are:
7
4x
5a + b
3(2m + 1)
In Grade 7, the focus is on linear expressions. A linear expression is a sum of terms that are either rational numbers or a rational number times a variable (with an exponent of either 0 or 1). If an expression contains a variable, it is called an algebraic expression. To evaluate an expression, each variable is replaced with a given value.
Equivalent expressions are expressions for which a given value can be substituted for each variable and the value of the expressions are the same.
An equation is a statement that two expressions are equal. An equation can be true or false. To solve an equation, students find the value of the variable that makes the equation true.
Students solve an equation that involves finding 10% of a number. They see that finding 10% of the number is the same as finding 0.1 of the number, or finding of the number.
Goals and Learning Objectives
- Write expressions and equations to represent real-world situations.
- Evaluate expressions for given values of a variable.
- Use properties of operations to write equivalent expressions.
- Solve one-step equations.
- Check the solution to an equation.
Ideal Weight
Lesson Guide
Have students work in pairs for this task. Students should look at the image, read the introduction, and estimate the weights of the two brothers.
ELL: When monitoring students, pay special attention to ELLs to ascertain that they are on task and clear about what needs to be done.
Mathematics
- Informally discuss the definition of a rule of thumb.
- Students use a rule of thumb to estimate the weights of Sultan Kösen and his brother Hasan.
- Subtracting 100 from a person's height to estimate the person's weight is an example of a rule of thumb.
Interventions
Student writes the algebraic expression 100 − h to represent a person's weight when h represents the person's height.
- Substitute the height of the tall man (251 cm) for h. Does the value of the expression make sense?
Opening
Ideal Weight
This man, Sultan Kösen, is one of the tallest men on Earth. He is 251 cm tall, and his brother Hasan, who is standing next to him, is 178 cm tall.
A rule of thumb is an easy-to-remember guide for making an estimate.
One rule of thumb is that an adult’s ideal weight in kilograms is 100 less than his or her height in centimeters.
- Use this rule of thumb to estimate the weights in kilograms of Sultan Kösen and his brother.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will evaluate expressions and solve equations to find measurements of height and weight.
Opening
Evaluate expressions and solve equations to find measurements of height and weight.
Adult Ideal Weight
Lesson Guide
Have students work in pairs to complete this activity.
Interventions
Student writes the algebraic expression 100 − h to represent a person's weight when h represents the person's height.
- Substitute the height of the tall man (251 cm) for h. Does the value of the expression make sense?
Student has difficulty in getting started with writing an expression to find a person's height when given that person's weight.
- What do you know?
- What are you trying to find?
Student does not know how to solve the equation to find height of a person when given that person's ideal weight.
- Can you solve the equation by just looking at it and trying to find the value of h?
- What number can you add to both sides of the equation so that the variable will be alone on one side of the equation?
Student has a solution.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problems.
Student has an incorrect solution
- Have you checked your work?
- Does your answer make sense?
- What does h stand for?
Possible Answers
- Using the rule of thumb:
h − 100
150 − 100 = 50
The ideal weight is 50 kg. - For an adult with an ideal weight of 30 kg:
h − 100 = 30
h = 130
The height is 130 cm.
Work Time
Adult Ideal Weight
Use this rule of thumb: an adult’s ideal weight in kilograms is 100 less than his or her height in centimeters.
- Let h = an adult’s height in centimeters. Write an algebraic expression for the person’s ideal weight in kilograms. Evaluate your expression to find the ideal weight, in kilograms, for an adult who is 150 cm tall.
- Write and solve an equation to find the height, in centimeters, of an adult who has an ideal weight of 30 kg.
Hint:
- An algebraic expression can combine arithmetic operations, numbers, and letters. Letters are used to represent variables. These are examples of algebraic expressions that contain variables: a , 3b , and 4x + 5. The variables in the expressions area ,b , andx .
- To evaluate an algebraic expression, replace each variable in the expression with a number and find the value of the expression. For example, to evaluate the expression 4 x + 5 whenx = 7, replacex with 7 and find the value of 4 • 7 + 5, which is 28 + 5, or 33
- An equation is a statement where two expressions are equal. It is formed by placing an equals sign between the two equivalent expressions
- To solve an equation, find the value of the variable that makes the equation true.
Weight in Pounds
Lesson Guide
Have students work in pairs to complete this activity.
ELL: For this task, encourage students to explain their ideas to one another. Math language must be used. Encourage the use of English without discouraging students from using their primary language(s).
Interventions
Student has difficulty in getting started with writing an expression for a person's weight, in kilograms, when they know the person's weight, in pounds, is p.
- What do you know?
- What are you trying to find?
Student has a solution.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problems.
Student has an incorrect solution
- Have you checked your work?
- Does your answer make sense?
- What does h stand for?
Possible Answers
- p ÷ 2 − 0.1(p ÷ 2)
- Possible answers:
- 51.75 kg
- 110 lb
Work Time
Weight in Pounds
Many people in the United States know their weight only in pounds. There is a rule of thumb that can help you use your weight in pounds to estimate your weight in kilograms: divide your weight in pounds by 2, and then subtract 10% of that number from the result.
- Let p = a person’s weight in pounds. Write an expression for the person’s weight in kilograms.
- Can you write an equivalent expression for the person’s weight in kilograms?
- Use the rule of thumb to find the weight, in kilograms, of a person who weighs 115 lb.
- Use the rule of thumb to find the weight, in pounds, of a person who weighs 49.5 kg.
Hint:
- Equivalent expressions are expressions that have the same value when a given value is substituted for the variable. For example, 3(x + 6) and 3x + 18 are equivalent expressions. Whenx = 2, both expressions have the value 24.
- If you have 80 pounds, how do you take 10% of it?
- How might you use the distributive property to write equivalent expressions?
- Now think back to the difference between an expression and an equation. To find a person’s weight in kilograms, do you need to evaluate an expression or solve an equation?
- To find a person’s weight in pounds, do you need to evaluate an expression or solve an equation?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion:
- Students with both correct and incorrect solutions (discussing the incorrect solutions can clear up misconceptions students may have)
- Students who can make viable arguments about whether or not an expression can be used to represent a person's weight, in kilograms, when the person's weight, in pounds, is known
- Students who solve the Challenge Problem
SWD: Participating in a whole-class discussion can be intimidating for students with language-based learning vulnerabilities and/or learning challenges. Supports for students during this portion of the lesson include:
- Prompt students to discuss their ideas, the questions posed, and what has taken place during the lesson with a partner or small group before sharing out in the whole class setting.
- Conference with individual students prior to the discussion to ascertain what they might be able to successfully contribute to the discussion. Encourage students to rehearse their contribution or to write notes as a reference for when they speak. This will support students with expressive language difficulties and/or students who are anxious or reluctant to participate in class discussions.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Allow students to ask questions to encourage presenters to be as precise and clear as possible.
Mathematical Practice 4: Model with mathematics.
- Students use expressions and equations to show mathematical relationships.
Mathematical Practice 6: Attend to precision.
- Look for students who use precise language and the properties of operations to explain why or why not an expression could be used to represent the weight in kilograms given the weight in pounds. Allow students to ask questions to encourage presenters to be as precise and clear as possible.
Challenge Problem
Answer
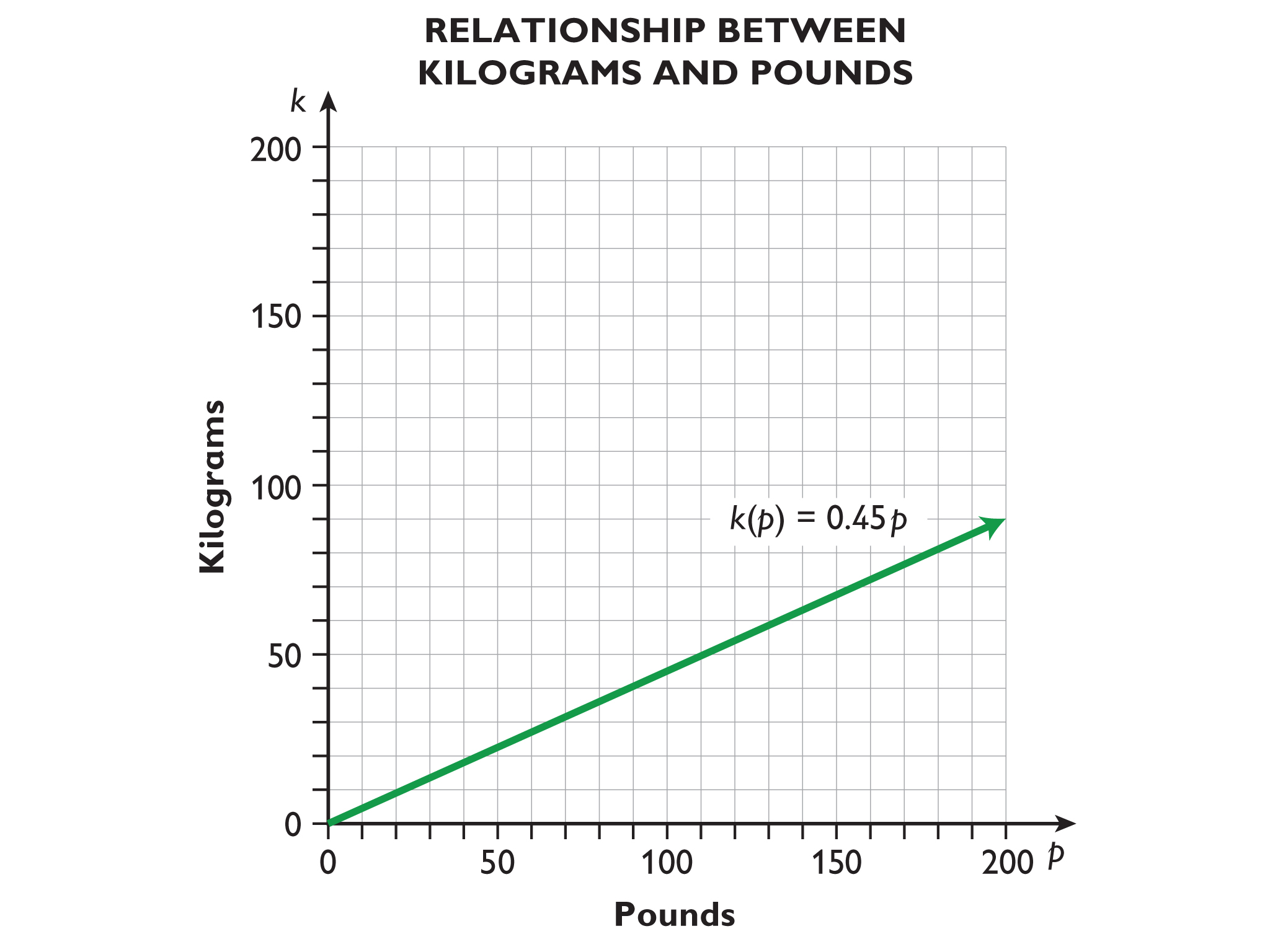
- k = 0.45p
- The point corresponding to the person weighing 115 lb is (115,51.75), so this person's weight, in kilograms, is 51.75 kg. The point corresponding to the person weighing 49.5 kg is (110,49.5), so this person's weight, in pounds, is 110 lb.
Work Time
Prepare a Presentation
Explain your solutions for the weight in kilograms and in pounds. Use your work to support your explanation.
Challenge Problem
To estimate your weight in kilograms, divide your weight in pounds by 2 and then subtract 10% of that number from the result.
Let p = weight in pounds. Let k = weight in kilograms.
- Write an equation for the relationship between k and p.
- Now draw a graph to show the relationship between k and p. Let p be the independent variable.
- Use the graph to find the weight in kilograms of a person who weighs 115 lb and the weight in pounds of a person who weighs 49.5 kg.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson informally. Ask the following questions:
- When is it helpful to use a rule of thumb?
- How did you evaluate the expression to find the ideal weight, in kilograms, for an adult 150 cm tall?
- How do you know whether to use an expression or an equation?
- How do you find the expressions or equations?
- How do you know when two expressions are equal?
- How is evaluating an expression different from solving an equation?
- How can you check the solution to your equation?
Ask students to share the expressions they wrote to represent a person's weight in kilograms. Ask:
- Why does the expression represent the given situation?
ELL: Use a pace that is appropriate for ELLs when posing these questions, especially when using words that students have recently learned. Allow ELLs to use a dictionary if they wish.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ strategies for writing and evaluating expressions and for writing and solving equations.
Hint:
As your classmates present, ask questions such as:
- How did you know whether to use an expression or an equation?
- How did you find the expression (or equation)?
- How can you check the solution to your equation?
- How do you know whether two expressions are equivalent?
Expressions and Equations
Lesson Guide
Have students work in pairs to read and discuss the summary of the math and answer the questions in the Hints section. It may be helpful to have students create examples of the following:
- Expressions
- How to evaluate expressions
- Equivalent expressions
- Equations
- How to solve an equation
ELL: When listening to pairs interact, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a foreign language. Be sure to listen for meaning and not correctness of grammar. Encourage students to ask each other probing questions if the meaning is not apparent. This partner time will help students during reflection time.
Formative Assessment
Summary of the Math: Expressions and Equations
Read and Discuss
An expression can combine arithmetic operations with numbers, letters, or both. Letters are used to represent variables.
- To evaluate an expression, find the value of the expression by replacing each variable in the expression with a given number.
- Two expressions are equivalent if they represent the same amount. When a given value is substituted for each variable (such as x), equivalent expressions have the same value.
- An equation is a statement that two expressions are equal. Every equation is composed of two expressions linked by an equal sign.
- To solve an equation, find the value of the variable that makes the two sides of the equation equal.
Hint:
Can you:
- Describe the differences between an expression and an equation?
- Explain what it means to evaluate an expression?
- Explain what it means to solve an equation?
- Explain what it means for expressions to be equivalent?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to make sure that students understand expressions and equations and how they are different.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think an expression is different from an equation because …