- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Flying Backward
Forward, Backward, or Hovering
Algebraic Reasoning

Overview
Students explore the effects of wind on a plane's time and distance and represent these situations using algebraic expressions and equations. They use terms with positive, negative, and zero coefficients.
Key Concepts
In this lesson, students show what they remember from Grade 6 about writing expressions and solving one-step equations. They use what they learned earlier in Grade 7 about adding and subtracting integers. They extend these concepts to write and interpret an expression with a negative coefficient.
Goals and Learning Objectives
- Review addition and subtraction of integers.
- Review the relationship between distance, time, and speed.
- Write an algebraic expression for distance in terms of time, t.
- Write a term with a negative coefficient.
- Review solving a one-step equation using the multiplication property of equality.
Flying Backward
Lesson Guide
Have students watch the video with a partner.
Mathematics
Students will give reasons why a plane can fly backward or hover over an area. Allow students to share their thoughts.
Opening
Flying Backward
Watch the video.
How can a plane fly backward or hover over an area?
VIDEO: Flying Backward
Speed
Lesson Guide
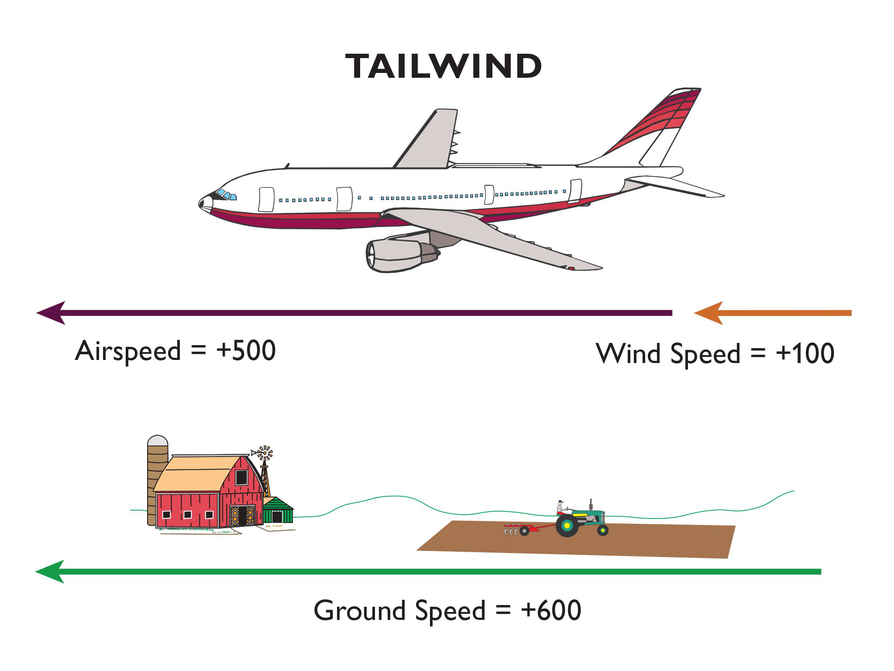
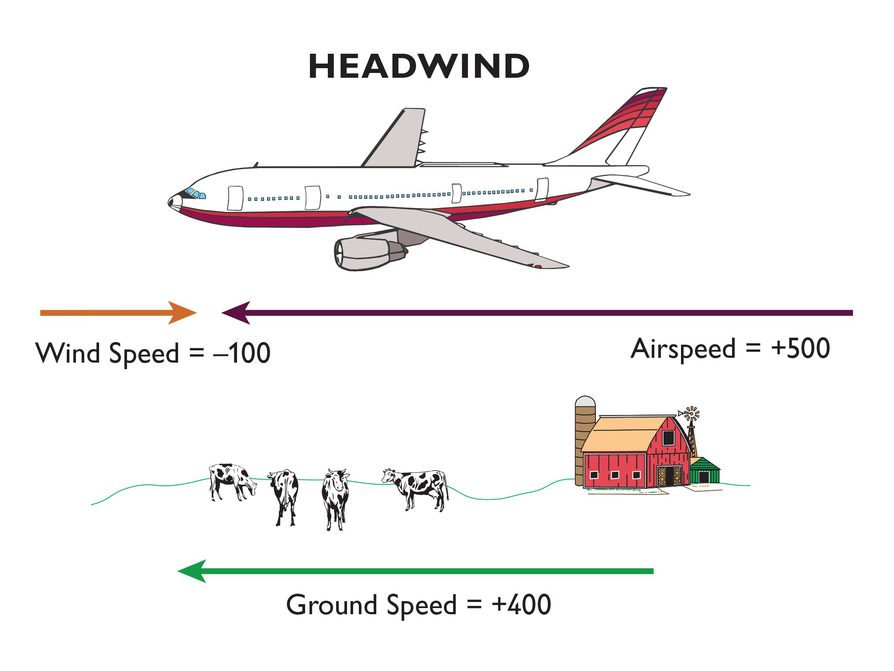
Next, have students look at the diagrams to understand the effects of a headwind or tailwind on a plane's airspeed and ground speed.
Ask questions such as, “How could we use addition of integers to represent the speed of the airplane in the first diagram? The second diagram?”
Mathematics
- Since a headwind is moving in the direction opposite the direction the plane is trying to fly, it is represented as a negative number.
- Since a tailwind is moving in the direction that the plane is trying to fly, it is represented as a positive number.
Interventions
Student does not understand what is meant by headwind and tailwind.
- Look at the pictures. How are the pictures alike? How are they different?
- Which wind will make the ground speed faster? Why?
Student does not understand the circumstances that would result in a plane standing still.
- If a plane is hovering or is still, what distance is it traveling?
- What numbers can you add or subtract to get a result of 0?
Student does not recall the rules for adding and subtracting integers.
- When you add numbers with different signs, how do you determine the sum?
- Can you draw a model for adding +2 and –7 (or subtracting 7 from 2)?
Student has a solution.
- Explain your strategy for solving the problem.
- Could we have used another method for solving the problem?
ELL: Create visual supports (digital cue cards, notes, or anchor charts) from the Intervention questions, so if students are struggling you can offer verbal prompting and explanation as well as a visual representation of the information.
Opening
Speed
Look at the two diagrams. Think about the relationship between airspeed, wind speed, and ground speed.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore relationships between air speed, wind speed, and time of flight.
Opening
Explore relationships between air speed, wind speed, and time of flight.
Expression for Distance
Lesson Guide
Make sure students understand what they are to do. To complete the table they need to tell whether the plane is flying forward, backward, or hovering. Then they need to write an expression for distance for three different situations.
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
- Students who, when considering a tailwind, add the two speeds
- Students who, when considering a headwind, write the tailwind speed as negative and add to the airspeed, or they subtract the speed of the tailwind from the airspeed
- Students who recall that distance can be found by multiplying the speed by the time
- Students who may be able to explain the relationship between the units: miles/hour, time, and miles
- Students who can explain how they used an equation to help them draw their conclusions
- Students may realize that if the headwind is greater than the airspeed, the distance traveled will be negative and this will translate to moving backward. If the headwind and airspeed are the same, the distance traveled will be 0t, and this will translate to the plane hovering. Be sure to discuss this practice in Ways of Thinking.
Interventions
Student does not understand what is meant by headwind and tailwind.
- Look at the pictures. How are the pictures alike? How are they different?
- Which wind will make the ground speed faster? Why?
Student does not understand the circumstances that would result in a plane standing still.
- If a plane is hovering or is still, what distance is it traveling?
- What numbers can you add or subtract to get a result of 0?
Student does not recall the rules for adding and subtracting integers.
- When you add numbers with different signs, how do you determine the sum?
- Can you draw a model for adding +2 and –7 (or subtracting 7 from 2)?
Student has a solution.
- Explain your strategy for solving the problem.
- Could we have used another method for solving the problem?
Possible Answers
- Forward: Plane A, d = 800t; Plane B, d = 600t; Plane E, d = 800t; Plane F, d = 650t
Backward: Plane D, d = −100t
Hovering: Plane C, d = 0t - Moving forward: coefficient of t is positive
Backward: coefficient of t is negative
Hovering: coefficient of t is 0
Work Time
Expression for Distance
Complete the table.
- From the information in the table, determine whether each plane is flying forward, flying backward, or hovering.
- Then choose one plane that falls into each of these categories, and write an equation that represents distance traveled. Let t = time in hours.
- Describe the coefficient of t when a plane is flying forward, flying backward, or hovering.
HANDOUT: Forward, Backward, or Hovering
Hint:
- Remember: In the expression 3 x , 3 is the coefficient ofx .
- Think about whether the wind and the plane are going in the same or opposite direction.
- If you know a plane is flying 500 miles per hour, how do you represent the miles it has flown in t hours?
Amelia Earhart
Lesson Guide
Remind students that they need to think about how distance, time, and speed are related when answering the questions after the Amelia Earhart video.
SWD: If students seem unsure of the task, model the steps for solving the problems before asking them to do the problems themselves.
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion:
- Students who can explain how they used an equation to help them draw their conclusions
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who construct viable arguments to support their answers related to the questions regarding Amelia Earhart's speed.
Interventions
Student does not understand the task.
- What does the paragraph tell you about Amelia Earhart's plane?
- How can you figure out her average speed?
Student doesn't know what the word average means.
- If you went 100 miles in 2 hours, how would you find your average miles per hour?
Student has a solution.
- Explain what you learned about headwinds and tailwinds. How might they affect average speed?
Possible Answers
- If the 2,020-mile flight took 15 hr, the average speed of Amelia Earhart's flight was a little less than 135 mph. Her average speed was less than the average speed for a Lockheed Vega.
- Answers may vary. Since the typical speed for the plane is 155 mph, there was probably a headwind with an approximate average speed of 20 mph, because a headwind slows a plane down.
Work Time
Amelia Earhart
Amelia Earhart was the first woman in history to fly solo from North America to Europe. On May 20, 1932, she flew from Newfoundland to Ireland—a distance of 2,020 miles. It took her nearly 15 hours to make the trip. The average speed for a Lockheed Vega—the plane that Amelia flew—is 155 miles per hour (mph).
View this video footage of Amelia Earhart before her flight around the world.
- How does the average speed of a Lockheed Vega compare to Amelia’s average speed?
- What factor(s) might have affected her average speed?
VIDEO: Amelia Earhart
Hint:
Write an equation to help you find Amelia’s average speed.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson informally. Ask questions such as the following:
- How did you calculate the distances? Explain the difference in the calculation when there is a tailwind versus a headwind.
- How did you decide whether to add or subtract the values for airspeed and wind speed?
- Why does 800t represent the distance in miles, where t represents the time in hours?
- How do you write an equation to find Amelia's speed, s? (2,020 = 15s)
- Can you explain the relationship between distance, time, and speed? (distance = time ⋅ speed)
ELL: Call on ELLs and encourage them to participate, even if their pace is slower or they are reluctant to volunteer due to their weaker command of the language.
Performance Task
Ways of Thinking: Make Connections
Take notes about the expressions and equations your classmates wrote and their strategies for solving the problems.
Hint:
As your classmates present, ask questions such as:
- Explain the difference in your equation when you had a headwind versus a tailwind.
- How did you decide whether to add or subtract the values for airspeed and wind speed?
- Can you explain why 800 t represents the distance in miles, wheret represents time in hours?
- Can you write an inequality that would represent Amelia’s actual time versus her theoretical time?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to determine where students have questions about expressions and equations.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about expressions and equations is …