Solving Percent Problems With Algebraic Expressions

Overview
Students see how different expressions for percent of increase and percent of decrease problems represent different ways to solve these problems. Students use equivalent algebraic expressions to solve percent problems.
Key Concepts
Students have previously solved percent of increase and percent of decrease problems. In this lesson, they look at how percent problems can be represented by algebraic expressions. Seeing the relationship of these problems to various equivalent algebraic expressions helps students relate different ways of solving problems involving percent of increase or percent of decrease.
For example, the sale price of a pair of jeans with original price p and discount of 10% can be represented as p − 0.1p, or just 0.9p. The first expression leads to a way of solving the problem in two steps; the second expression leads to a one-step solution. Similarly, the total price of an item with a cost c dollars and 5% tax can be written as c + 0.05c, or just 1.05c.
Goals and Learning Objectives
- Solve percent of increase and percent of decrease problems using equivalent algebraic expressions.
Construction Site
Lesson Guide
Have students read the information about the construction site. Have them look closely at both the illustration and the diagram. Ask the following questions:
- Do you see the road on the upper left that has no intersections? Point to it. Point to where the road is represented in the diagram.
- Do you see the roads that divide the “top” and “bottom” sides of the square into three parts? Point to where these roads are represented in the diagram. What is the ratio of the parts?
- How is the lower-right road divided? What is the ratio of the parts?
Have students talk with a partner about how they might estimate the percent of the total area that is represented by Rectangle A.
SWD: This lesson uses images to present information. Make sure students have the ability to customize the display of this information (this may entail simplifying the amount and/or type of information presented at one time, zooming out, zooming in, etc.).
Opening
Construction Site
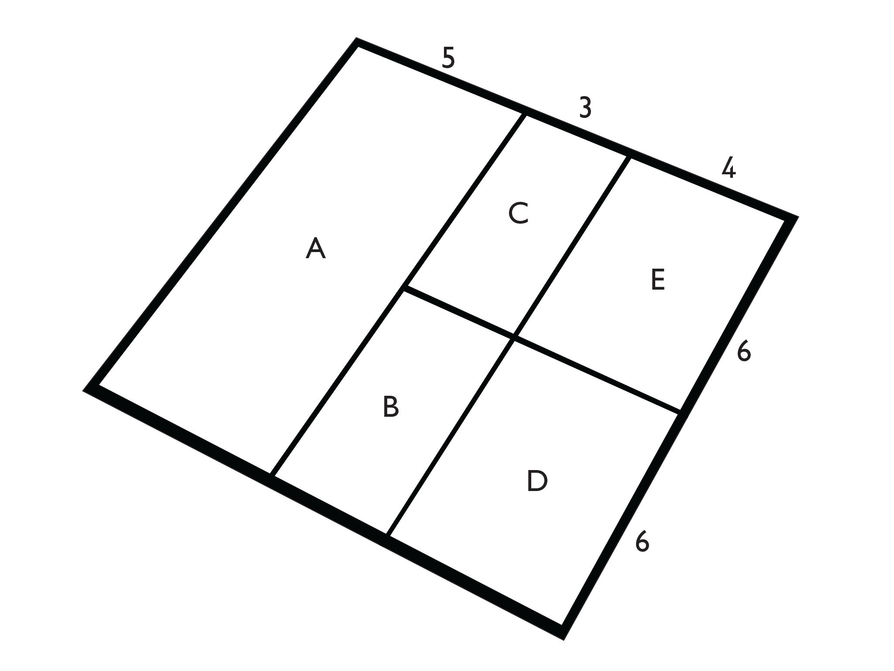
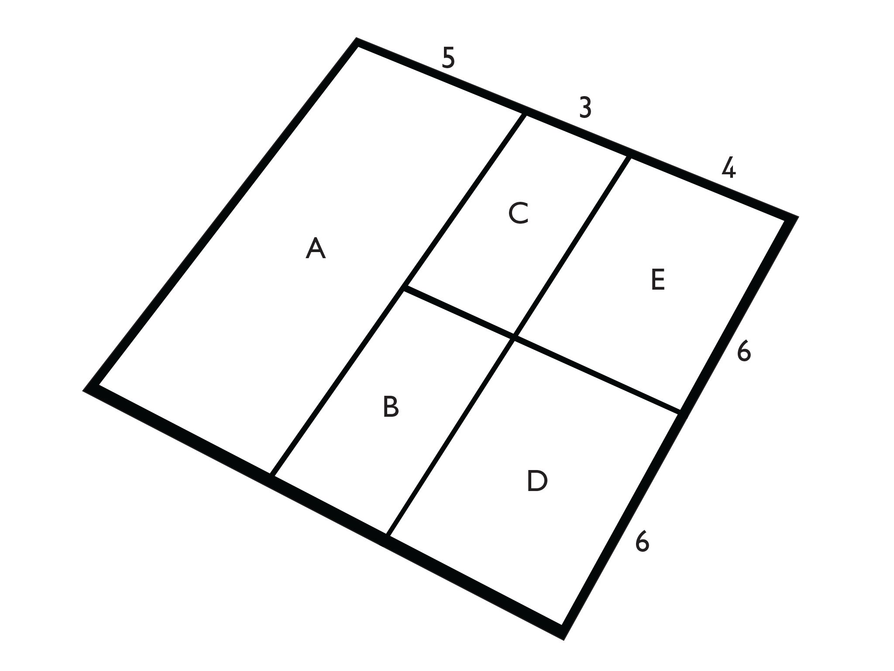
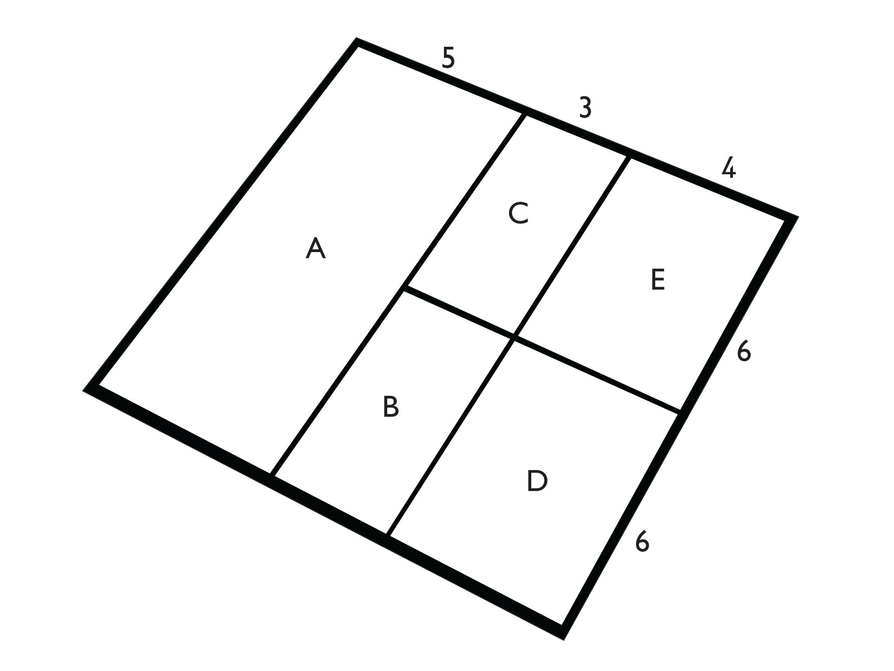
This image shows an overhead view of a construction site. In the illustration, you can see roads that form rectangles within a square.
On the upper-left side of the square is a road that has no intersections. The roads that form the “top” and “bottom” sides of the square have intersections that divide each road into three parts in the ratio 5:3:4. The lower-right road is divided into two parts in the ratio 6:6. These ratios are shown in the diagram.
You cannot determine the actual length of each side of the square based on the information provided; however, assume that the length is 12 units.
- Without calculating, estimate the percent of the total area of the square that is represented by Rectangle A.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will represent percent problems in different ways using equivalent algebraic expressions.
Opening
Represent percent problems in different ways using equivalent algebraic expressions.
Percent of Area
Lesson Guide
Have students work in pairs to calculate the percent of the total area that is represented by Rectangle A. Ask a few questions to make sure students understand the task.
SWD: Students with disabilities may have difficulty working with decimals and percents, especially moving between the two. If students demonstrate difficulty to the point of frustration, provide direct instruction on the basics for finding equivalent fractions, decimals, and percents.
Interventions
Student does not know how to begin to calculate the area represented by Rectangle A.
- Use the diagram.
- Calculate the area in square units for the whole square and for Rectangle A.
- How can you use the two areas to answer the question?
Answer
- Rectangle A is of the total area. The area of Rectangle A is 60 square units.
The area of the square is 144 square units.
Work Time
Percent of Area
Calculate the percent of the total area of the square that is represented by Rectangle A.
Analyze Construction Site
Lesson Guide
Have students remain in pairs to assess whether the architect's claim is true. Ask students the following:
- What is the area of Rectangle A?
- How can you represent the areas of Rectangles B + C + D + E?
- Should you use fractions or decimals?
- What is simplest form?
Interventions
Student does not know where to begin in determining whether the architect's claim is true.
- What does it mean for one rectangle to be 40% larger than another rectangle?
- What is the area of Rectangle A?
- How can you find the area of the rectangle made up of Rectangles B, C, D, and E?
Possible Answers
- The architect's claim is true. Looking at the diagram, the area of Rectangle A is 60 square units.
The area of Rectangles B + C + D + E is 84 square units.
40% of 60 is 24 (0.40 ⋅ 60 = 24)
The area of Rectangles B + C + D + E is 40% larger than Rectangle A.
Work Time
Analyze Construction Site
An architect claims that the larger rectangle with buildings on it (made up of the four smaller rectangles, B + C + D + E) is 40% larger than the plain grass rectangle (Rectangle A).
- Is the architect’s claim true? Explain why or why not.

Which Expression?
Lesson Guide
Have students remain in pairs to work on this activity.
Interventions
Student does not see the relationship between 40% and 25.
- What fraction can you write for 40%?
- How do you write that fraction in simplest form?
Possible Answers
The following do represent the area:
a + 25a; a + 0.4a; 1.4a; 125a; (1 + 25)a; (1 + 0.4)a
The following do not represent the area:
(1 + 14)a; 1 + 0.4a
1.4a and 125a are written in simplest form.
(1 + 0.4a is also in simplest form, but does not represent the area.)
- Yes and not in simplest form
- Yes and not in simplest form
- Yes and in simplest form
- Yes and in simplest form
- No and not in simplest form
- Yes and not in simplest form
- Yes and not in simplest form
- No and in simplest form
Work Time
Which Expression?
Let a = the area of Rectangle A.
For each of the following expressions, write whether it does or does not represent the area of the large rectangle with buildings (Rectangles B + C + D + E) and figure out if it is written in simplest form.
- a + 25a
- a + 0.4a
- 1.4a
- 125a
- (1 + 14)a
- (1 + 25)a
- (1 + 0.4)a
- 1 + 0.4a
Hint:
- Think about equivalent expressions and the relationships between percents, fractions, and decimals.
- Expressions in simplest form do not have parentheses.
Prepare a Presentation
Preparing for Ways of Thinking
As students are working, look for students who have a thorough understanding about the relationship between percents, fractions, and decimals. These students can share their work during the Ways of Thinking discussion.
Identify students who did the Challenge Problem so that they can share their work during the Ways of Thinking discussion.
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Students begin with one expression that represents the percent of increase situation. They then decontextualize by manipulating the expression into different forms without necessarily attending to the problem situation. In this process, they identify an expression in simplest form that can now be used to represent the percent of increase situation. They can then contextualize and look back at the problem to see that this simplified expression provides a new way of looking at a percent of increase (or a percent of decrease) problem—a way to solve the problem using only one step.
Challenge Problem
Answer
- The original price was $12.50.
The equation 0.80x = 10 can be used to solve the problem algebraically.
Work Time
Prepare a Presentation
Be prepared to explain and justify the algebraic expressions you used to describe the construction site.
Challenge Problem
Could you use either of these equations to find the original price, in dollars, of a T-shirt, if the sale price after a 20% discount is $10?
0.80x = 10
or
1.2 ⋅ 10 = x
Make Connections
Mathematics
Facilitate the discussion to help students make sense of the math. Encourage students to explain their responses. Ask questions such as the following:
- How do you calculate the area of the large square? (6 + 6)(5 + 3 + 4) = 144 square units
- How do you calculate the area of rectangle A? 5(6 + 6) = 60 square units
- How do you find what percent 60 is of 144? Some possible methods:
- Solve the proportion: = x100.
- Solve an equation: 144x = 60, write the answer as a decimal or as a fraction, and then rewrite the answer as a percent.
- Write in simplest form, , and then write as a decimal, ; finally write it as a percent, % or .
- How do you determine if the architect's claim is true? Which two rectangles are we talking about? What methods could you use to compare the area of the rectangles?
- The area of rectangle A is 60 square units, and 40% of 60 is 24. The area of the rectangle which has the buildings is 7 × 12, or 84 square units, so the architect's claim is true.
- Begin with the area of rectangle A and multiply by 1.4.
- Use 25 for 40%.
- Which expressions cannot be used to represent the rectangle with the buildings? Why?
- Is this expression, a + 0.4a in simplest form? Why?
- In the Challenge Problem, which equation do you use to find the original cost of the t-shirt? Why?
ELL: When calling on students, be sure to call on ELLs and to encourage them to actively participate even if they are feeling reluctant because their pace may be slower.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ explanations and justifications for the algebraic expressions they used to describe the construction site.
Hint:
As your classmates present, ask questions such as:
- How do you know that 40% and 0.4 are equivalent?
- Where did the 1 come from in (1 + 0.4) a ?
- Why isn’t a + 0.4 a in simplest form?
Percent Problems
Lesson Guide
Use this activity to check students' understanding of solving problems about percent of increase or percent of decrease in just one step. After students complete the problems, you may want them to solve these additional problems:
- Find the total price, in dollars, of a $30 bicycle after a 5% sales tax. ($31.50)
- Find the sale price, in dollars, of a bicycle with an original price of $30, after a 25% discount. ($22.50)
Possible Answers
- 1.05x
- 0.75x
Work Time
Percent Problems
Write an expression in simplest form that represents each situation.
- The price, in dollars, of a bicycle, after a 5% sales tax, if the price before tax is x dollars
- The sale price, in dollars, of a bicycle, on sale for 25% off, if the original price is x dollars
Hint:
Your expression should have only one term.
Equivalent Expressions
Lesson Guide
Have each student write a Summary of the Math in this lesson, then write a class summary. When done, if you elect the summary is helpful, share it with the class.
A Possible Summary
Different equivalent expressions can show different ways to solve problems involving percent of increase or percent of decrease.
The following two expressions show the sale price of a book with the original price of x dollars, after a 25% discount:
- x − 0.25x
- 0.75x
You can use either to find the sale price of a $10 book:
- $10 − 0.25 ⋅ $10 = $10 − $2.50 = $7.50
- 0.75 ⋅ $10 = $7.50
If you use the second expression, 0.75x, the one in simplest form, you only need to calculate once.
Formative Assessment
Summary of the Math: Equivalent Expressions
Write a summary about how you used equivalent expressions to solve percent problems.
Hint:
Do you explain how equivalent expressions can help you solve percent increase or percent decrease problems?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to ascertain students' understanding of how percents are used in everyday situations.
SWD: Some students may struggle to determine the salient information from the presentations. Provide students with summaries to reinforce the key ideas from the presentations. It will also model for students how to create strong summaries of mathematical information.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
An everyday situation in which I might use percents is …