Peer Review

Overview
Students work with a partner to revise their work on the Self Check. Students work with their partner to do activities that involve using expressions and equations to solve problems.
Key Concepts
Students will use what they have learned so far in this unit about writing expressions as well as writing and using equations to solve problems.
Goals and Learning Objectives
- Use expressions and equations to solve problems.
Critique
Lesson Guide
Students should look at the results of their Self Check task and the questions under the critique section.
SWD: Some students with disabilities may struggle with self-assessment; use your knowledge of student strengths and vulnerabilities to inform and create interventions you will put into place for this period of class time.
Opening
Critique
Review your work on the Self Check problem and think about these questions:
- What does x represent?
- How else could you write the expression 4(x + 7)?
- How do you write 1 more than x using algebra?
- How can you check whether your value for x is correct?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will apply what they know about writing expressions and equations and using them to solve problems.
Opening
Apply what you know about writing expressions and equations and using them to solve problems.
What Is the Number?
Lesson Guide
Organize students into pairs. Have partners help each other revise their work based on the feedback they received. Then the students work together on a task very similar to the a task on the Self Check.
Support students as they work. Try not to make suggestions that move students to a particular approach. Instead, ask questions that help students clarify their thinking.
If students find it difficult to get started, these questions might be helpful:
- What questions were you asked for feedback?
- How could you and your partner work together to address one or more of those feedback questions?
If several pairs of students are struggling with the same issue, you could write a relevant question on the board. You might ask a student who has performed well on a particular part of the task to help a pair that is struggling. If students are struggling with the new task, have them begin by reviewing the corresponding part of the previous task.
Preparing for Ways of Thinking
While students work, note different approaches to the task such as the following:
- How do students organize their work?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
Look for students who organized their work in different ways to present during the Ways of Thinking discussion. Look for both correct and incorrect solutions to be presented.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of each problem and what it is asking them to do. They must plan and carry out a solution strategy. After they solve a problem, they need to go back and check that their solution makes sense. Students also have the opportunity to work with another student and try to understand his or her approach to the problems.
Mathematical Practice 6: Attend to precision.
Students are asked to present their work in a clear, precise way. They should try to use correct mathematical language and symbols and to carefully label their work so it is easy to follow.
Possible Answer
- The number is 14. This can be found using either 3(x + 8) = 66 or 3x + 24 = 66. Suppose x represents the number that I am thinking of. If I add 8, I have x + 8. If I multiply that number by 3, I have 3(x + 8). If I know the number is equal to 66, I need to solve the equation 3(x + 8) = 66. Since 3(x + 8) is equal to 3x + 24 by the distributive property, I could also solve the equation 3x + 24 = 66.
To solve the equation,
3x + 24 = 66
3x + 24 + (−24) = 66 + (−24)
3x = 42
x = 14
x represents the number I am thinking of: 14.
Work Time
What Is the Number?
Use what you learned from the Self Check problem to approach this similar task. Work with your partner.
I am thinking of a number. When I add 8 and then multiply by 3, the result is 66. What is my number?
- Which of the equations represent this problem? Select all that apply, and justify your choices.
x + 24 = 663
x + 24 = 66
3x + 8 = 66
3(x + 8) = 66
- For each equation that you identified, find the value of x and explain what it represents.
Three Consecutive Numbers
Lesson Guide
Continue as you did on Task 3.
Possible Answer
- The correct expressions are:
3x + 3x + 3 + 3x + 6 and 3x + 3(x + 1) + 3(x +2) The consecutive numbers are 17, 18, and 19. To determine the three consecutive numbers, solve either of the equations below:
3x + 3x + 3 + 3x + 6 = 162
9x + 9 = 162
9x = 153
x = 17
or
3x + 3(x + 1) + 3(x + 2) = 162
3x + 3x + 3 + 3x + 6 = 162
9x + 9 = 162
9x = 153
x = 17
Work Time
Three Consecutive Numbers
Suppose three consecutive numbers are added together, and the sum is then multiplied by 3.
- Which of the following expressions represent this situation? Select all that apply, and justify your choices.
3x + 3x + 1 + 3x + 2
3x + 3(x + 1) + 3(x + 2)
3x + 3x + 3 + 3x + 6
x + x + 3 + x + 6
- The total is 162. What are the three consecutive numbers? Explain your answer.
Figure and Expressions
Lesson Guide
Continue as you did on Task 4.
Possible Answer
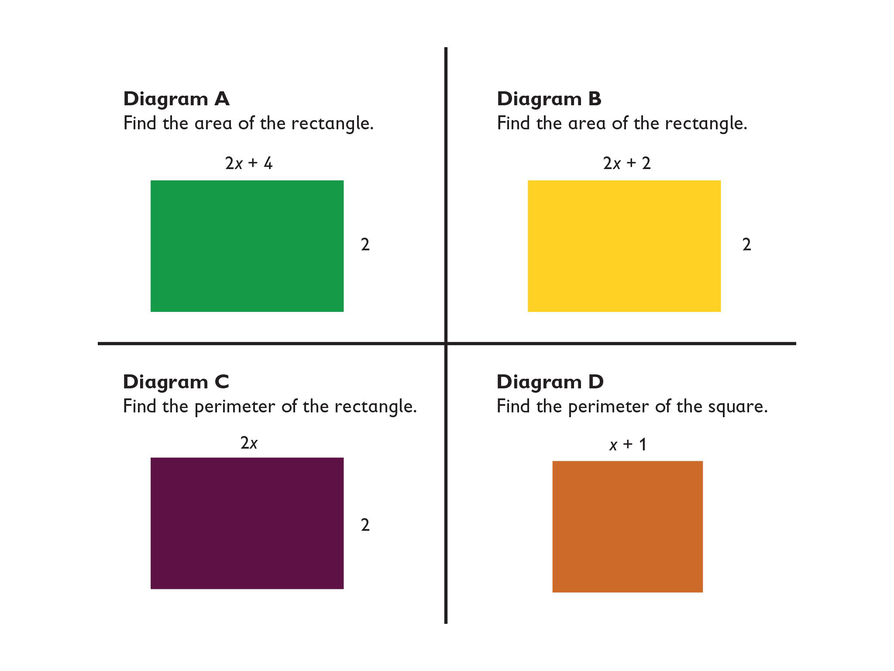
- Diagram A does not describe the algebraic expression 4x + 4.
- The area of the figure in Diagram A is 2(2x + 4). Therefore, 4x + 8 represents the area of Diagram A.
Work Time
Figure and Expressions
- Which figure(s) do not represent the expression 4x + 4?
- Explain your answer.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson informally. As you discuss each of the problems, ask questions such as the following:
- How did you organize your work?
- What strategy did you choose?
- How do you know if that strategy works?
- What did you do if your strategy did not work?
- How did you write the equation to solve the problem?
- How did you solve the equation?
- How can you explain your answer?
SWD: As students present their solutions, make connections between different solutions to the same problem. This allows students to see the multiple ways to solve/analyze a problem. Write down the important connections, and have students copy into their Notebook. ELL: Provide ELLs and other students a sample or model for the concepts, strategies, and applications that will be addressed in the assessment, and the format you want them to follow. Be prepared to address and explicitly reteach or review vocabulary, concepts, strategies, and applications.
Performance Task
Ways of Thinking: Make Connections
Take notes about the approaches your classmates used to write expressions and equations to represent and solve the problems.
Hint:
As your classmates present, ask questions such as:
- How did you organize your work?
- In solving the problems, did you ever choose a strategy that was unproductive? If so, what did you do?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to find out what students have learned that helps them solve equations.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I have learned that has really helped me to solve equations is …