Geometric Expressions

Overview
Students write expressions for geometric situations. They examine how different equivalent expressions can show different ways of thinking about the same problem.
Key Concepts
Students use their previous knowledge of how to find the perimeter and area of squares and rectangles. They write algebraic expressions for the perimeter and area of geometric figures. They examine how equivalent expressions, used to represent a problem situation, give clues to the approach the writer of the expression used to solve the problem. In the Challenge Problem, they use the distributive property to find the solution.
ELL: For ELLs, access prior knowledge by writing the words area and perimeter on the board. Have students create concept maps associated with area and perimeter. Record students' responses on large poster paper that you can display in the room. The goal is to generate a list of words that students can use as a reference.
Goals and Learning Objectives
- Access prior knowledge of how to find the perimeter and area of squares and rectangles.
- Write algebraic expressions for finding perimeter or area of figures.
- Identify equivalent expressions.
Perimeter of Tiles
Mathematics
Partners work together to write an expression for the perimeter of a rectangle that is made up of 5 tiles. Be sure students understand that each tile is a square with side length x, and that the tiles are placed next to each other with no space in between.
Before moving to Work Time, allow some students to share their expressions and how they generated them. Correct expressions may include x + 5x + 5x + x, 2(5x) + 2x, or any expression equivalent to 12x. Be sure to include some students who wrote an incorrect expression so that the other students can help identify errors or misconceptions.
SWD: Help students with disabilities make connections between what they have learned in previous tasks about area and perimeter and writing algebraic expressions.
Opening
Perimeter of Tiles
Each square tile has side length x.
- Write an expression for the perimeter of the rectangle that is made up of the 5 tiles.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will write equivalent expressions that represent the perimeters and areas of geometric figures.
Opening
Write equivalent expressions that represent the perimeters and areas of geometric figures.
Perimeter of 100 Tiles
Lesson Guide
Have students work with a partner on this activity.
Interventions
Student has difficulty getting started.
- What are you trying to find?
- Is each side of the tile part of the perimeter?
Student has an incorrect solution.
- How can you check that your expression is correct?
- Does your answer make sense?
- What does x stand for?
Possible Answers
- Correct expressions will vary, but will be equivalent to 202x.
Work Time
Perimeter of 100 Tiles
Write an expression for the perimeter of the rectangle that is 100 tiles long.
Hint:
- Think about how you found the perimeter of the rectangle that was 5 tiles long.
- Use the same reasoning to write an expression for the perimeter of the rectangle that is 100 tiles long.
Student Work
Lesson Guide
Have students work with a partner on this activity.
Interventions
Student does not understand the expressions.
- Point out that x can stand for any number.
- Try to draw a picture of what each expression represents. Does that picture show the perimeter?
Possible Answers
- Expressions A, B, and D are correct.
- Yes. All three of the expressions are equivalent to 202x.
- 202x
Work Time
Student Work
The image shows four expressions that Sophie, Jack, Kevin, and Marcus wrote for the perimeter of the rectangle that is 100 tiles long.
- Which three expressions are correct?
- Are the three correct expressions equivalent? Explain.
- What is an expression for the perimeter that has only one term?

Hint:
- Are any of the four expressions equivalent to the expression you wrote?
- Think about how you might use properties of operations (associative, commutative, and distributive) to identify equivalent expressions.
- Look for an expression with only one term. Can you write it in a simpler way?
Match Approach and Expression
Lesson Guide
Have students work with a partner on this activity.
Interventions
Student has difficulty getting started.
- Look at a statement. Think about how you would write an expression to represent that expression using x as the length of a side of the tile.
Possible Answers
Kevin: Expression D
Jack: Expression B
Sophie: Expression A
Work Time
Match Approach and Expression
Each student’s statement below describes a different way of thinking about how to express the perimeter of the rectangle that is 100 tiles long.
Read how these students approached the problem in order to write an expression.
Kevin: I added the lengths of the sides of the rectangle.
Jack: I added the length and width and then multiplied by 2.
Sophie: I saw that the first and last squares had 3 sides as part of the perimeter, but all of the other squares had only 2 sides in the perimeter.
- Match each correct expression from the image with each of the three students’ statements.
Area and Perimeter
Lesson Guide
Have students work with a partner on this activity.
Interventions
Student confuses perimeter and area.
- Think about the word rim in perimeter.
- Review definitions of perimeter and area.
Possible Answers
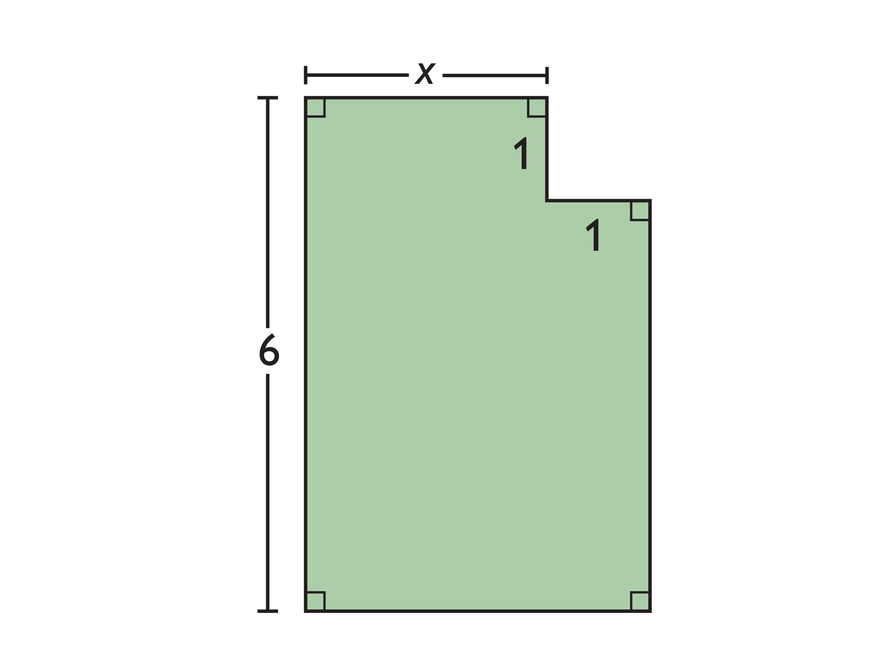
Expressions for perimeter:
x + 6 + (x + 1) + 5 + 1 + 1
2 ⋅ 6 + 2(x + 1)
or any expression equivalent to 2x + 14
Expressions for area: 6(x + 1) − 1
5(x + 1) + x
or any expression equivalent to 6x + 5
Work Time
Area and Perimeter
Look at the figure.
- Write an expression for the perimeter.
- Write an expression for the area.
Hint:
- What values do you add to find the perimeter?
- What is the length of the bottom of the figure?
- How do you find the area of a figure?
- How could you use subtraction to find the area?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion:
- Students who approach the activities in different ways (this will provide different expressions to analyze during Ways of Thinking)
- Students who attempt the Challenge Problem even if their approach does not lead to a correct answer (discussing their errors will provide worthwhile discussion)
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who can explain how their expression matches the problem or who can critique the explanations of other students.
Mathematical Practice 4: Model with mathematics.
This lesson provides an opportunity for students to write algebraic expressions to represent mathematical relationships.
Mathematical Practice 6: Attend to precision.
Students should use precise mathematical language.
Challenge Problem
Answer
- Side of equilateral triangle: 4x + 8
Side of square: 3x + 6
Work Time
Prepare a Presentation
- Choose from Sophie’s, Jack’s, Marcus’s, or Kevin’s solutions to the problem of 100 tiles.
- Compare and contrast your solution with the solution you chose.
Challenge Problem
An equilateral triangle and a square both have the same perimeter:
12x + 24
- Find the length of a side of the equilateral triangle and the length of a side of the square.
Hint:
Think about how to use the distributive property and common factors.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson. Encourage students to explain their responses. Ask questions such as the following:
- How did you connect your expression to the figure?
- How do you know that two expressions are equivalent?
- Could you use the properties of operations (associative, commutative, and distributive) to identify equivalent expressions? Explain.
- How did you match the approaches of the three students to the expressions for the perimeter of the rectangle made up of 100 tiles?
- What formulas did you use to find the perimeter and area of the figure?
- How do you find the perimeter of a figure?
- How do you find the area of a figure?
- Could you use subtraction to find the area of the figure?
- How did you use factoring or the distributive property to solve the Challenge Problem?
SWD: Students must feel safe enough to share their ideas, strategies, and, most importantly, mistakes. Most students—and students with disabilities in particular—are not used to talking about mathematics; yet in higher-level courses, student success might depend on participation in study groups and the student's ability to share ideas.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ strategies for writing equations for the perimeter and area of geometric figures.
Hint:
As your classmates present, ask questions such as:
- How did you connect your expression to the figure?
- How did you know that two expressions were equivalent?
- How did you match the approaches of the three students to the expressions for the perimeter of the rectangle made up of 100 tiles?
- What formulas did you use to find the perimeter and area of a figure?
Equivalent Expressions
Lesson Guide
Have each student write a Summary of the Math in this lesson, then write a class summary. When done, if you elect the summary is helpful, share it with the class.
A Possible Summary
In this lesson, I wrote algebraic expressions for the perimeter and the area of a figure. Depending upon how I thought about the problem, I generated different expressions. All of the expressions for the same problem are equivalent. This means that no matter what value we give the variable, all of those expressions will have the same value.
Formative Assessment
Summary of the Math: Equivalent Expressions
Write a summary about equivalent expressions.
Hint:
Check your summary:
- Do you explain what equivalent expressions means?
- Do you discuss how properties of operations can be used to identify equivalent expressions?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to determine if students understand how properties of operations are used to create equivalent expressions.
ELL: Allow additional time for ELLs to discuss the reflection with a partner before writing, to help them organize their thoughts. Allow ELLs who share the same primary language to discuss in their language of choice, and to use a dictionary (or dictionaries).
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Properties of operations are used to create equivalent expressions because …