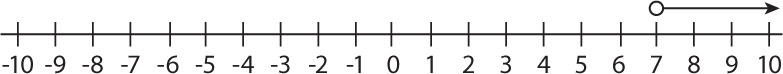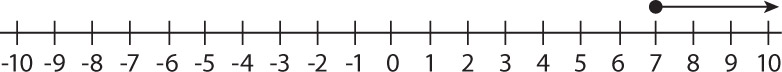- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Graph an Inequality
Graph an Inequality
Graphing Inequalities
Negative Coefficients
Representing Inequalities on a Number Line
Solving & Graphing Inequalities

Overview
Students discover how the addition and multiplication properties of inequality differ from the addition and multiplication properties of equality.
Students use the addition and multiplication properties of inequality to solve inequalities. They graph their solutions on the number line.
Key Concepts
In this lesson, students extend their knowledge of inequalities from Grade 6. In Grade 6, students learned that solving an inequality meant finding which values made the inequality true. Students used substitution to determine whether a given value made an inequality true. They also used a number line to graph the solutions of inequalities. By graphing these solutions on a number line, they saw that an inequality has an infinite number of solutions.
Now, in Grade 7, students work with inequalities that also contain negative numbers and learn to solve and graph solutions for inequalities such as −2x − 4 < 5. This involves first understanding how the properties of inequality differ from the properties of equality. When multiplying (or dividing) both sides of an inequality by the same negative number, the relationship between the two sides of the inequality changes, so it is necessary to reverse the direction of the inequality sign in order for the inequality to remain true. Once students understand this, they can apply the same steps they used to solve equations to solve inequalities, but remembering to reverse the direction of the inequality sign when multiplying or dividing both sides of the inequality by a negative number.
Goals and Learning Objectives
- Access prior knowledge of how to solve an inequality.
- Observe that when multiplying or dividing both sides of an inequality by the same negative number, the inequality sign must change direction.
- Solve and graph inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers.
Properties of Inequality
Lesson Guide
Students work in pairs to discover what happens when the same number (positive or negative) is added to both sides of an inequality. They also discover what happens when both sides of the inequality are multiplied by the same number (positive or negative).
Mathematics
Students should discover that when they add the same number (either positive or negative) to both sides of the inequality, the inequality is still true. When they multiply both sides of the inequality by a positive number, the inequality is still true. But, when they multiply both sides by a negative number, the direction of the inequality sign must be reversed.
To test this property, you may want to provide additional samples. For example, you can provide the inequality 8 > −4 and have students use the following operations on both sides: add 7, add −7, multiply by 7, and multiply by −7.
ELL: Use every opportunity for students to practice their math reasoning skills. This task is also an opportunity for you to model effective oral and written language structures necessary for language development. Explicitly teach students how to state whether or not the inequality is true or false.
Opening
Properties of Inequality
You have been using the addition and multiplication properties of equality to help you solve equations.
Addition Property of Equality
You can add any number to both sides of an equation and the result will be a true equation.
Multiplication Property of Equality
You can multiply both sides of an equation by any number and the result will be a true equation.
Today you will work with inequalities. For the inequality –3 < 4, discuss what happens when you add or multiply as specified.
- Add 2 to each side.
- Add –2 to each side.
- Multiply each side by 2.
- Multiply each side by –2.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will discover how the processes for solving inequalities and solving equations are similar and different.
Opening
Discover how the processes for solving inequalities and solving equations are similar and different.
Numeric Inequalities
Lesson Guide
Have students work in pairs.
Interventions
Student does not know the rules for computing with integers.
- Can you model that operation using a number line?
- Can you model that operation using a drawing?
Student cannot identify the sides of the inequality.
- Think of the inequality symbol like a wall separating both sides of the inequality.
Student concludes that the sign must be reversed when any operation involving a negative number is involved.
- Try again. Begin with −4 < 2. What is the result when you add −2 to both sides?
- What is the result when you subtract −2 from both sides?
Answers
- −5 < 2
When subtracting a positive number, the inequality remains true. - −1 < 6
When subtracting a negative number, the inequality remains true. - −32 < 2
When dividing by a positive number, the inequality will remain true. - 32 > −2
When dividing by a negative number, the inequality symbol must change direction for the inequality to remain true.
Work Time
Numeric Inequalities
Again start with –3 < 4. For each problem, predict if the inequality will remain true. Then verify your predictions.
- Subtract 2 from both sides.
- Subtract –2 from both sides.
- Divide both sides by 2.
- Divide both sides by –2.
Algebraic Inequalities
Lesson Guide
Have students work in pairs. Students use an interactive to graph the solution to the inequality on a number line. Make sure that students understand the task.
SWD: Create a learning chart for inequalities with the written definitions of <, >, ≤, and ≥, and examples of each.
Interventions
Student does not know how to graph the inequality.
- Since the solution is x > 7, where would you find values greater than 7 on the number line?
Possible Answer
- Both sides of the inequality are divided by 7 (or multiplied by ).
- Answers will vary.
Work Time
Algebraic Inequalities
Look at this solution.
2x > 14
x > 7
- Explain each step in finding the solution.
- Graph the inequality on the number line.
- Check your work by using values from the number line in the original inequality.
INTERACTIVE: Graph an Inequality
Hint:
Think about whether the graph should have a closed circle or an open circle.
Justify Steps and Graph
Lesson Guide
Have students continue working in pairs.
Interventions
Student cannot justify the steps.
- What can you do to both sides of the inequality to go from the inequality on the first line to the inequality on the second line?
Possible Answers
- In the first step, 6 was added to both sides of the inequality. In the second step, both sides of the inequality were divided by 3 (or multiplied by ).
- Answers will vary.
Work Time
Justify Steps and Graph
Look at this solution.
3x − 6 ≥ 15
3x ≥ 21
x ≥ 7
- Explain each step in finding the solution.
- Graph the inequality on the number line.
- Check your work by using values from the number line in the original inequality.
HANDOUT: Representing Inequalities on a Number Line
INTERACTIVE: Graph an Inequality
Negative Coefficients
Lesson Guide
Have students continue working in pairs.
Interventions
When one side of an inequality contains a negative number by itself, and both sides of the inequality are multiplied by a positive number, student thinks the sign needs to be reversed.
- Just think about what number you chose when you did your computation on both sides.
Student may confuse multiplying or dividing by a fraction with multiplying or dividing by a negative number.
- Think about multiplying or dividing both sides of 8 > 4 by .
Possible Answers
- In the first step, –2 was added to both sides of the inequality. In the second step, both sides of the inequality were divided by –4, or multiplied by −. Since we divided by a negative number (or multiplied by a negative number), the inequality sign is reversed.
- Answers will vary.
Work Time
Negative Coefficients
Look at this solution.
−4x + 2 > 10
−4x > 8
x < −2
- Explain each step in finding the solution.
- Graph the inequality on the number line.
- Check your work by using values from the number line in the original inequality.
HANDOUT: Negative Coefficients
INTERACTIVE: Graph an Inequality
Fractions in Inequalities
Lesson Guide
Have students continue working in pairs.
Interventions
Student can't justify the steps.
- What can you do to both sides of the inequality to go from the first step to the second step?
- How can you make the x into a 1x, or x?
Student does not know how to graph the inequality.
- Since the solution is x is greater than or equal to –10, where would you place your closed circle?
- How would you show x is greater than –10?
Student uses 0 to check their work.
- What might be a good number to put into the inequality to check it?
- Should you try numbers on both sides of –10?
Possible Answer
- In the first step, –4 was added to both sides of the inequality. In the second step, both sides of the inequality are multiplied by 2 (or divided by ). Since we multiplied (or divided) by a positive number, the inequality sign does not change.
- Answers will vary.
Work Time
Fractions in Inequalities
Look at this solution.
- Explain each step in finding the solution.
- Graph the inequality on the number line.
- Check your work by using values from the number line in the original inequality.
HANDOUT: Fractions in Inequalities
INTERACTIVE: Graph an Inequality
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who may be making errors and drawing incorrect conclusions, as well as students who are making correct discoveries. For example, a common misconception is for students to incorrectly assume that any operation involving a negative number will result in the need to reverse the inequality sign. When students make a generalization, encourage them to try other examples to test their generalization.
Look for students who are uncertain as to how > and ≥ are alike and different. You may want to include an explanation of the symbols in the Ways of Thinking discussion.
Identify pairs of students who attempt the Challenge Problem.
SWD: Posters help students by fostering group work and peer tutoring. Students can represent the concepts visually, helping them to discuss and refine their ideas and understanding.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students analyze what happens when operations are applied to both sides of an inequality. To do this, they need to be able to break the situation into cases (addition of a positive number, addition of a negative number, subtraction of a positive number, and so on.) and then proceed to examine each case separately. To justify their conclusions, they will need to provide examples and counterexamples. When evaluating the arguments of others, they will need to identify when an argument is flawed.
Challenge Problem
Answer
Work Time
Prepare a Presentation
- Summarize your learning about working with inequalities.
- Support your conclusions with examples of your work.
Challenge Problem
Solve this inequality:
Hint:
Think about how addition and subtraction are related and how multiplication and division are related.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson informally. Encourage students to explain their responses. Ask questions such as the following:
- What does solving an inequality mean?
- Why did you change the direction of the inequality sign?
- How do you decide if the graph should be an open circle or a closed circle?
- How is multiplying or dividing by a negative number the same?
- How is adding or subtracting the same?
- If the inequality symbol were an equal sign, how would your answer be similar? How would it be different?
- What happens to an inequality if you add or subtract the same number to both sides? Why?
- What happens to an inequality if you multiply or divide both sides by the same positive number? Why?
- What happens to an inequality if you multiply or divide both sides by the same negative number? Why?
If any students attempted the Challenge Problem, have them share their solutions whether or not their solutions are correct. This inequality differs from those the students just solved because it has the variable on both sides of the inequality. The goal is to get the variable alone on one side and a number on the other side.
ELL: Provide ELLs with sentence frames to support them in building arguments and critiquing. Examples would be “I think that the inequality is true because.…” or “My reasoning behind my solutions are.…”
Examples for critiques would be “I don't quite understand how you came to the conclusion that..… since.…” or “Please explain to me how you came to that conclusion since I can’t see it myself.”
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' explanations for solving each inequality and summarize them into the properties of inequalities.
Hint:
As your classmates present, ask questions such as:
- What does solving an inequality mean?
- Why did you change the direction of the sign?
- How did you decide whether or not to fill in the circle on the number line?
- If the inequality symbol was an equals sign, how would your answer be similar? How would it be different?
Solve Inequalities
Lesson Guide
Have students read the addition property of inequality and the multiplication property of inequality. Ask several volunteers to provide examples of each property. Then have students work individually to solve the inequalities. Allow time for work to be checked by substituting three values into the original inequality: the value which makes both sides equal, one value less than that, and one value greater than that. After they have finished, have students present their solutions to a partner.
Possible Answers
x + 6 > 3
x + 6 − 6 > 3 − 6 Addition property of inequality
x > −3
−4x ≥ 12
Multiplication property of inequality
x ≤ −3
4 − 2x < 12
4 − 4 − 2x < 12 − 4 Addition property of inequality
−2x < 8
Multiplication property of inequality
x > −4
3x + 4 ≥ 15
3x + 4 − 4 ≥ 15 − 4 Addition property of inequality
3x ≥ 11
Multiplication property of inequality
Work Time
Apply the Learning: Solve Inequalities
Addition Property of Inequality
You can add any number to both sides of an inequality and the result will be true.
Multiplication Property of Inequality
You can multiply both sides of an inequality by any positive number and the result will be true. If you multiply both sides of an inequality by a negative number, you will need to reverse the direction of the inequality sign in order for the inequality to be true.
Solve each inequality and represent on a graph. Check your solution by checking values.
- x + 6 > 3
- −4x ≥ 12
- 4 − 2x < 12
- 3x + 4 ≥ 15
INTERACTIVE: Graphing Inequalities
Hint:
Think about how you can check your work using the solution on the number line.
Properties of Inequality
Lesson Guide
Have each student write a summary of the math in this lesson, then write a class summary. When done, if you think the summary is helpful, share it with the class.
ELL: In posing these questions, if the student involved is an ELL, speak at a pace that is adequate and provide ample wait time to allow for a thoughtful response. Present the questions and responses in writing.
A Possible Summary
You can solve equations by using the addition and multiplication properties of equality. These properties allow you to add any number to both sides of an equation or multiply both sides of an equation by the same number and still have a true equation.
You can solve inequalities by using the addition and multiplication properties of inequality. The difference is that for inequalities, the multiplication property allows you to multiply both sides of the inequality by a positive number and still have a true inequality. But, if you multiply both sides of an inequality by a negative number, you have to reverse the direction of the inequality sign for the inequality to be true.
In solving both equations and inequalities, the goal is the same: to get the variable by itself on one side and a number on the other side.
Formative Assessment
Summary of the Math: Properties of Inequality
Write a summary of what you have learned about properties of inequality.
Hint:
Do you explain how solving inequalities is similar to and different from solving equations?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to get an understanding of what students have learned about concepts related to solving inequalities.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something new I learned today is...