Simplifying Expressions Using Distributive Properties

Overview
Students use the distributive property to simplify expressions. Simplifying expressions may include multiplying by a negative number. Students analyze and identify errors that are sometimes made when simplifying expressions.
Key Concepts
This lesson focuses on simplifying expressions and requires an understanding of the rules for multiplying negative numbers. For example, students simplify expressions such as 8 − 3(2 − 4x). These kinds of expressions are often difficult for students because there are several errors that they can make based on misconceptions:
- Students may simplify 8 − 3(2 − 4x) to 5(2 − 4x) because they mistakenly detach the 3 from the multiplication.
- Students may simplify 8 − 3(2 − 4x) to 8 − 3(−2x) in an attempt to simplify the expression in parentheses even though no simplification is possible.
- Students may simplify 8 − 3(2 − 4x) to 8 − 6 −12x. This error could be based on a misunderstanding of how the distributive property works or on lack of knowledge of the rules for multiplying integers.
Goals and Learning Objectives
- Simplify more complicated expressions that involve multiplication by negative numbers.
- Identify errors that can be made when simplifying expressions.
An Expression for Area
Lesson Guide
Have students work in pairs for this activity.
Mathematics
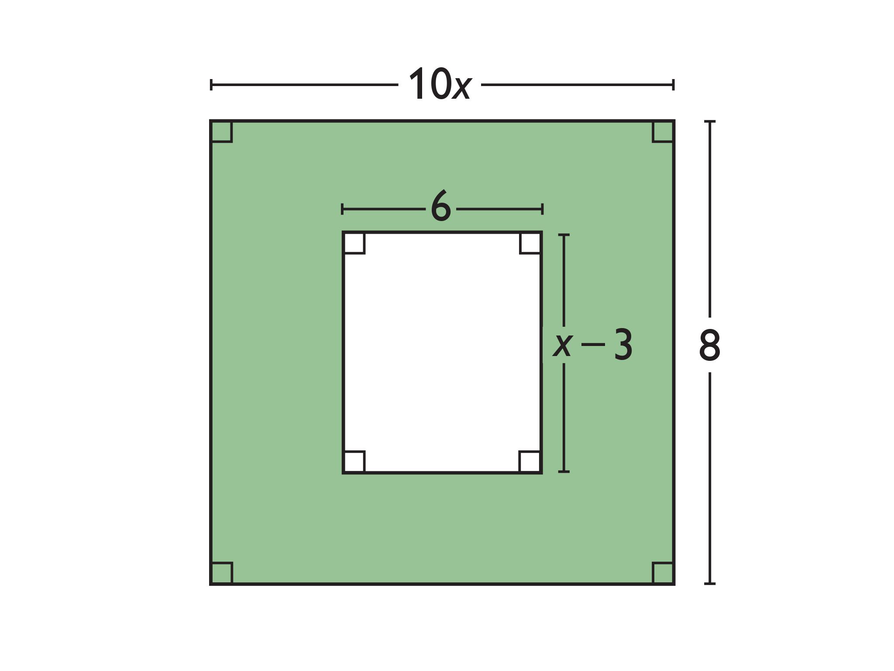
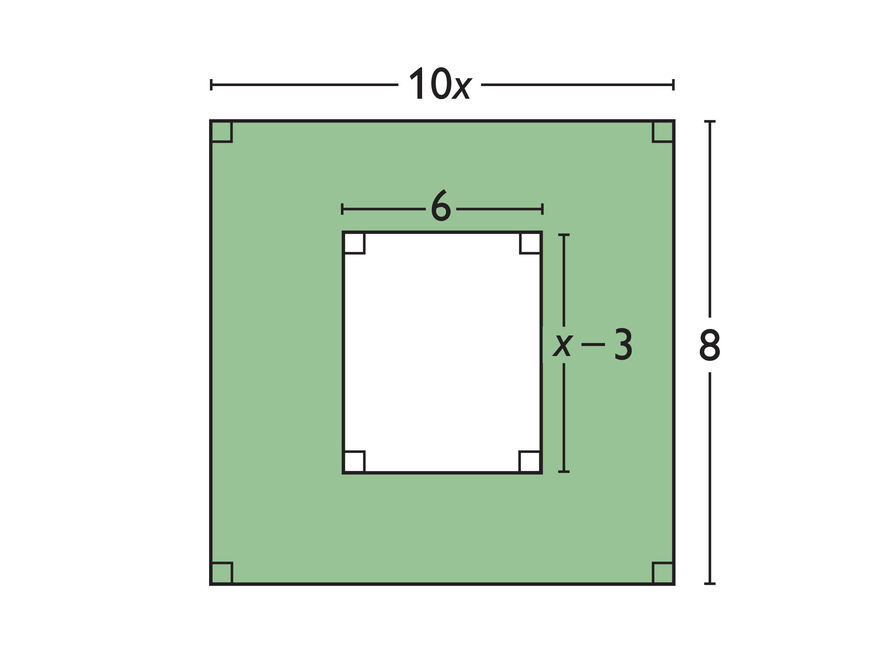
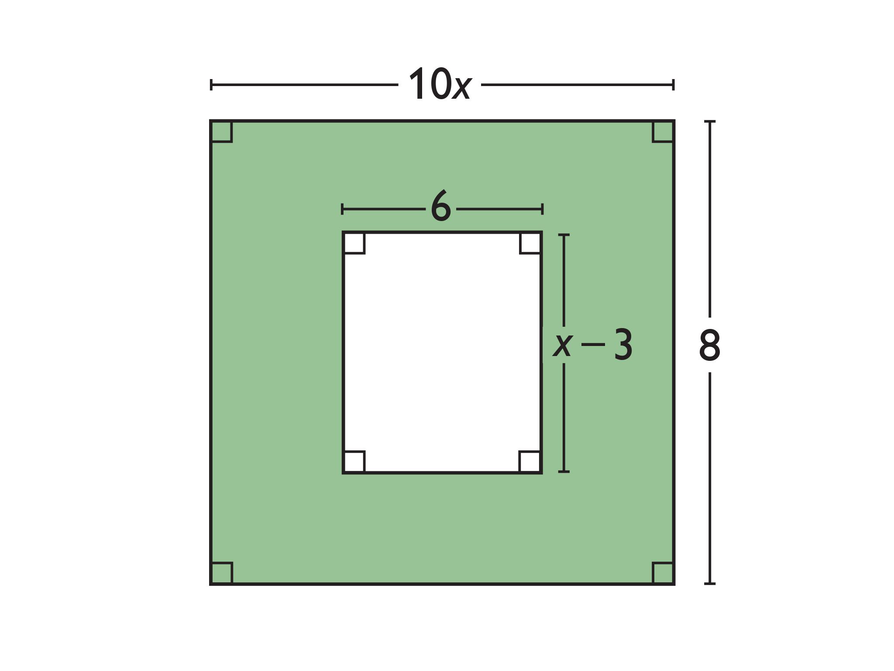
Allow time for student pairs to look at the figure and write an expression for the area of the shaded part of the figure. Students should all see that the expression (10x)(8) − 6(x − 3) can be used to represent the area.
Opening
An Expression for Area
Write an expression for the area of the shaded part of the figure.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will detect errors that can be made when simplifying expressions.
Opening
Detect errors that can be made when simplifying expressions.
Correct Work on Simplifying Expressions
Lesson Guide
Have students work with a partner on the activities. Ask a few questions to make sure that students understand what it means to simplify an expression:
- Should the simplified expression contain parentheses?
- How many terms of each variable should the simplified expression contain?
- How many numbers should the simplified expression contain?
- How can you use the distributive property to simplify an expression?
ELL: Provide scaffolding so that ELLs develop the vocabulary and English skills needed to provide written comments that describe common errors. Provide models and examples that are comprehensible.
Interventions
Student has difficulty getting started.
- Did all four students begin with the same expression?
- Look at one student's work at a time. Look at one line at a time. Do you see a mistake?
[common error] Student multiplies integers incorrectly.
- Make a list of the possible combinations of signs when multiplying two integers.
- How do you decide the sign of the product when you multiply two integers?
Student has a solution.
- Why did you approach the problem the way that you did?
- Explain your strategy.
- Could we have used another method to solve this problem?
Possible Answers
- Jack's solution is correct.
- The other students made the following mistakes: Karen found the difference of 8 − 6 before completing the multiplication. Lucy attempted to simplify x − 3 to −2x; x − 3 cannot be simplified. Marcus simplified −6(x − 3) to −6x − 18. He either misunderstood how the distributive property works or he did not know that multiplying two negative integers results in a positive product.
Work Time
Correct Work on Simplifying Expressions
Karen, Lucy, Jack, and Marcus each simplified the expression he or she wrote for this problem.
- Whose solution is correct?
- What mistakes did the other students make?

Hint:
- When you simplify an expression, write an equivalent expression that is as simple as possible. It should not contain any parentheses. It should have only one term with each variable and only one number without a variable. Examples:
2(x – 4) = 2x – 8
and
x + 5x + 4x = (1 + 5 + 4)x = 10x - Can you use the distributive property to rewrite expressions?
- Remember: Multiplying two negative integers results in a positive product.
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion:
- Students who are able to articulate the errors in the activity (choose these students as presenters in the Ways of Thinking discussion)
- Students who have misconceptions about simplifying expressions (discuss the misconceptions during the Ways of Thinking discussion)
- Students who attempt the Challenge Problem even if their answers are not correct (discussing their errors will provide worthwhile discussion)
- Students who justify the correct answer by substituting and evaluating each step to prove that the expressions for each step are equivalent
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Throughout this lesson students justify their answers and explain errors.
Mathematical Practice 6: Attend to precision.
Look for students who use precise mathematical language in their explanations.
Challenge Problem
Answers
- 4.5 and make sense.
- 2 does not make sense because the length of the inner rectangle would be –1, which is impossible. 14 does not make sense because the height of the inner rectangle would be 11, which is greater than the height of the outer rectangle.
Work Time
Prepare a Presentation
- Summarize the mistakes made by three of the students.
- For the correct answer, prove that all steps are equivalent expressions by using substitution.
Challenge Problem
Look again at the shaded figure.
- Which of these numbers make sense for a value of x?
4.5, 2, , 14
- Explain your reasoning.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson informally. Encourage students to explain their responses. Ask questions such as the following:
- How did you know to multiply or add those numbers?
- Did you consider whether your answer makes sense?
- Can you explain that step again?
- How can you use substitution to check for equivalent expressions?
- What does an expression in simplest form look like?
SWD: If you know that some students may need additional time and/or prompting to participate in this discussion, provide them several of the questions ahead of time (printed out or digitally).
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ strategies for simplifying expressions.
Hint:
As your classmates present, ask questions such as:
- How did you know to multiply/add those numbers?
- Did you check for equivalent expressions by substitution?
- Did you consider whether your answer makes sense?
- Can you explain that step again?
Recognize Equivalent Expressions
Lesson Guide
Have students work in pairs to answer the questions. Have each pair present their explanation of the answer to another pair.
Interventions
When working on the Apply the Learning tasks, the student's expressions are not equivalent.
- How did you simplify the problem (10 − 8) − 6(x − 3)?
- Compare your answer with the answer of another pair of students.
ELL: When forming groups, be aware of your ELLs and ensure that they have a learning environment where they can be productive. Different types of partnerships include:
- Pairing them up with English speakers so they can learn language skills.
- Pairing them up with students who are at the same level of language skills, so they can take a more active role and they can work things out together.
- Pairing them up with students whose proficiency level is lower, so they play the role of the “supporter.”
You can also pair them up based on their math proficiency.
Possible Answers
- Yes; (8) and (10x) can be switched because multiplication is commutative, and the additional brackets are not necessary but help clarify organization.
- Yes; again, multiplication is commutative and +(–6) and –6 have the same value; (–1)3 and –3 have the same value.
Work Time
Apply the Learning: Recognize Equivalent Expressions
Are each of the following expressions equivalent to (10x)(8) − 6(x − 3)?
Explain why or why not.
- (8)(10x) − [6(x − 3)]
- (8)(10x) + (−6)[x + (−1)3]
Check your work by substituting the value 10 for the variable x.
Hint:
Check your work by substituting the value 10 for the variable x .
Simplify Expressions
Lesson Guide
Have each student write a summary of the mathematics in this lesson, then write a class summary. When done, if you thing the summary is helpful, share it with the class.
A Possible Summary
In this lesson we continued to write expressions and simplify them. When you simplify an expression, you write an equivalent expression that is as simple as possible. It contains only one term with each variable and only one number without a variable. Expressions like 4x, 5a + 2, 7 − 5y, and 9 are all in simplest form. When you simplify an expression, you always get an expression equivalent to the original expression. You can check that the expressions are equivalent by substituting some values for the variable and checking that the original expression and the simplified expression have the same value.
When you use the distributive property to simplify an expression, you need to be careful. For example, when you simplify 8 − 3(x + 2), you have to be sure you multiply both x and +2 by –3, not just by 3.
Formative Assessment
Summary of the Math: Simplify Expressions
Write a summary about simplifying expressions.
Hint:
Check your summary:
- Do you explain how to use the distributive property to rewrite an expression?
- Do you discuss the importance of paying attention to plus and minus signs in multiplication?
- Do you describe how to check whether two expressions are equivalent?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to recognize additional questions that students may have regarding simplifying expressions as well as newly learned concepts that students understand.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starters below if you find them to be helpful.
Something new I learned today is …
I still have questions about …