Gallery Problems Exercise

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery Descriptions
Flight of the Albatross
Students use estimation to learn about the distances albatrosses fly.
Sales
Students use equivalent expressions to solve two-step percent of increase or percent of decrease problems in one step.
Carpet Cleaning
Students write and solve equations to model the relationship between hours worked and the cost of carpet cleaning.
Equations About Numbers
Students write an equation to solve a problem about the sum of three consecutive numbers. Then they write and solve their own problem about the sum of three consecutive numbers.
Equations About Sports
Students write and solve equations to solve problems about a basketball game and about walking versus bicycling.
Equations About Figures
Students write and solve equations to model the side lengths and areas of rectangles.
A Number Trick
Students use what they know about simplifying algebraic expressions to do number tricks.
Flight of the Albatross
Answers
- 24,901.45 miles is the circumference of the Earth at the equator, so approximately 25,000 miles is the circumference of the Earth around the equator.
- About zero miles at a pole if you were flying east to west (not north to south).
a. Estimates will vary but will generally be between 21,500 miles and 12,500 miles. The circumference of the Earth around the equator is approximately 25,000 miles. Justifications will vary based upon students’ methods of approximation. Students may approximate that the 30th south parallel is about one third of the distance from the equator to the South Pole.
b. Speed will vary based on the answer to problem 3(a) but will generally fall between 85 miles per hour and 50 miles per hour.
The important part of this task is the justifications the students give for their answers.
Work Time
Flight of the Albatross
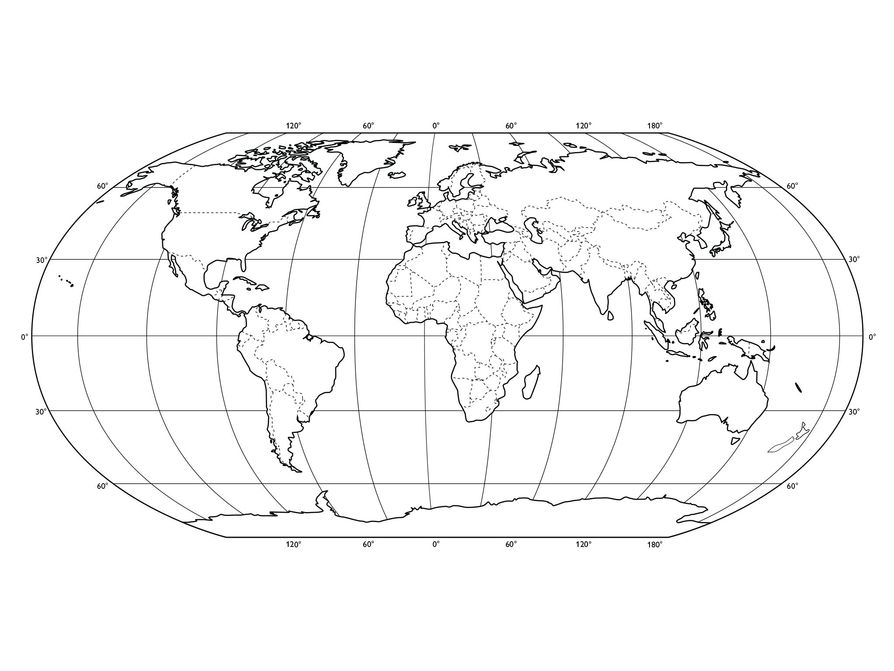
The albatross is a very large bird (with a wingspan of more than 12 feet). These feathered giants live near oceans, and New Zealand has a large number of them. An albatross can soar like no other bird. Recent research has shown interesting details about the behavior of the albatross in New Zealand. Some birds soar nearly continuously but just around their island. Another group migrates from New Zealand all the way to the Indian Ocean. The rest fly around the world, without landing, and return to their home base in as little as six weeks. There are also some albatross that continue, without landing, to soar for another trip around the globe.
Albatrosses fly so much that both getting into the air and landing are very difficult. They need some kind of a runway to take off, and landings are sometimes more like crashes.
Look at this coordinate system of the Earth.
You see the meridians (from the North Pole to the South Pole) and the parallels (parallel to the equator). New Zealand lies on the 45th parallel south.
- If you fly around the world going due east all the time, the maximum distance of the trip is about 25,000 miles. Explain why.
- What is the shortest distance around the world if you fly along a parallel?
Suppose an albatross flies within a band between the 30th south parallel and the 60th south parallel.
a. Estimate the distance around the Earth within this band. Think of ways to make an argument that your guess is correct.
b. The path of an albatross is not straight; the albatross does not make “direct flight.” Suppose the distance traveled by the albatross is four times the straight-line distance you estimated in problem 3(a), and the albatross completes the trip in six weeks. Estimate the albatross’s speed in miles per hour.
Sales
Answers
- Possible answer: No, because both stores don’t have the same original prices.
The best deal for running shoes is at Cheap Sports. The best deal for running shirts is at Sports Unlimited. The best deal for running shorts is at Sports Unlimited. The best deal for running socks is at Cheap Sports. - Sports Unlimited:
Cheap Sports: - 8% increase
Work Time
Sales
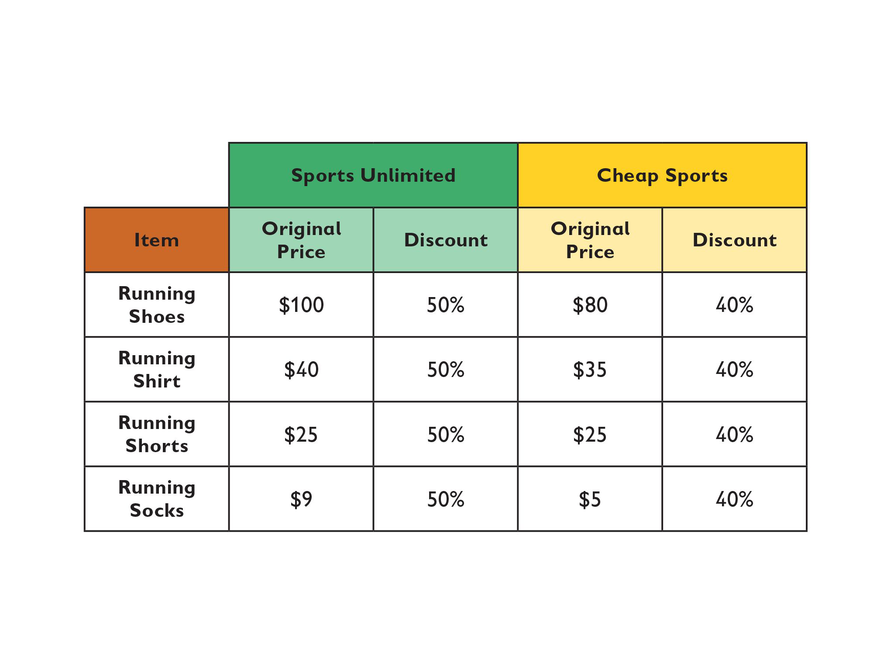
Sales, sales, sales! They are everywhere around you. You know the signs, and you know that you have to be careful.
Assume the items at both stores below are of the same quality.
Look at the two signs. Are you sure you get the best deals at the store that offers the 50% discount? Where can you get the best deal for each item?
Look at the following table.
If the original price per item at Sports Unlimited is a dollars, then the discount price can be expressed as a – 0.5a, or as (1 – 0.5)a.
If the original price per item at Cheap Sports is b dollars, then the discount price can be expressed in similar ways. Give the three ways the discount price at Cheap Sports can be expressed.
- After the sale, the stores get new collections, and prices go up. At Sports Unlimited, each price is now 5% greater than the original price. At Cheap Sports, each price is now 10% greater than the original price. Give three expressions for the new prices, using a notation similar to the notations used in problem 2.
Suppose the new price of an item can be expressed as follows:
1.08 • (original price)
What is the percent change from the original price?
Carpet Cleaning
Answers
- $260 is the total cost of the job.
- 6 hours
- $80 per hour
- $45 is the flat fee.
Possible answers:
Work Time
Carpet Cleaning
Mr. Adams’s brother owns a carpet cleaning business. Problems 1–4 show different jobs his company was hired to do. Answer the questions for each job using the following for each situation.
- Let a represent the flat fee, in dollars, for coming to the house.
- Let b represent the number of hours spent at the house.
- Let c represent the charge, in dollars, for each hour spent at the house.
- Let d represent the total cost, in dollars, of the job.
- Determine the total cost of a job.
- If a = 60, b = 4, and c = 50, write an equation for calculating the total cost, d, of this job.
- Solve your equation to find the total cost of this job.
- Determine the number of hours spent at the house.
- If a = 40, c = 30, and d = 220, write an equation for calculating the number of hours, b, the cleaners spent on this job.
- Solve your equation to find the number of hours the cleaners spent on this job.
- Determine the hourly charge for a job.
- If a = 50, b = 7, and d = 610, write an equation for calculating the charge, c, for each hour this job took.
- Solve your equation to find the hourly charge for this job.
- Determine the flat fee the cleaners charged for coming to a house.
- If b = 3, c = 35, and d = 150, write an equation for calculating the flat fee, a, the cleaners charged for this job.
- Solve your equation to find the flat fee the cleaners charged for this job.
- Write all the algebraic equations you can to show the relationships between a, b, c, and d for the carpet cleaning business of Mr. Adams’s brother.
Equations about Numbers
Answers
The three consecutive numbers are 64, 65, and 66.
- Possible problem: The sum of three consecutive whole numbers is 33. Find the three numbers.
Answer: 10, 11, 12
Work Time
Equations about Numbers
- The sum of three consecutive whole numbers is 195. Find the three numbers.
- Write a problem about the sum of three consecutive whole numbers. Give it to your partner to solve.
Equations about Sports
Answers
Sophie scored 11 points.
It will take his brother 16 minutes.
Work Time
Equations about Sports
- Sophie and Karen together scored 19 points in a basketball game. Karen scored 3 fewer points in the game than Sophie. How many points did Sophie score?
- Kevin starts walking from his home at a speed of 80 yards per minute. Kevin's brother starts out after Kevin on a bicycle 50 minutes later. His brother's speed is 330 yards per minute. How long will it take his brother to catch up to Kevin?
Equations about Figures
Answers
Confirm that
- Possible explanation:
The solution does not make sense. If , then . A negative number cannot be a length. - If :
- Larger rectangle: –24 centimeters by –11 centimeters
- Smaller rectangle: –9 centimeters by –2 centimeters
- Possible explanation:
- Possible answers:
Work Time
Equations about Figures
- A rectangle is 8 feet long and 6 feet wide. If each dimension is increased by the same number of feet, the area of the new rectangle is 80 square feet. Write an equation for the new rectangle, with x representing the increase in feet.
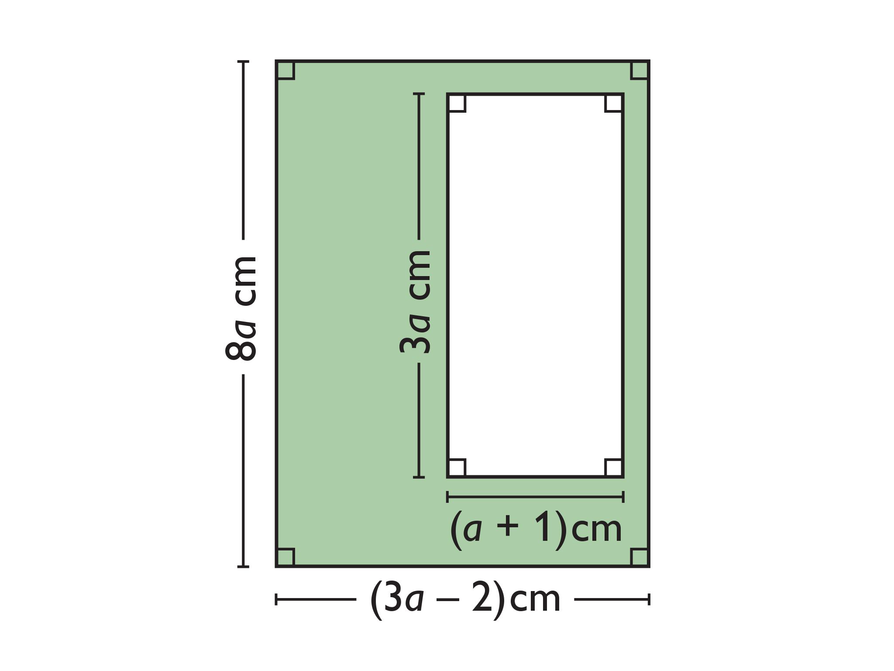
Here is an equation stating that the area of the shaded region is 260 square centimeters:
8a(3a – 2) – 3a(a + 1) = 260
Confirm that a = 4 is the solution to this equation.
- Marcus said, “If the area of the smaller, white rectangle in the figure is 246 square centimeters, a would have to equal –3.”
- Does this solution make sense? Why or why not?
- What would the dimensions of both rectangles in the figure be if a were equal to –3?
- A piece of wire 36 centimeters long is bent into the shape of a rectangle with a length that is twice its width. Write an equation for the width.
A Number Trick
A Number Trick
Answers
- The numbers students choose will vary.
The following expression shows what the student was asked to do with the number they chose.
- Answers will vary.
Work Time
A Number Trick
- Work with a partner. Give each of these directions to your partner, one at a time:
- Write down a number, but don’t let me see which number you wrote.
- Add 3 to your number.
- Multiply that sum by 5.
- Subtract 10 from that product.
- Divide that difference by 5.
- Subtract your original number from the quotient.
- The difference is 1. Am I correct?
- Use what you know about simplifying expressions to show why the trick works.
- Make up your own number trick. Try it with your partner.