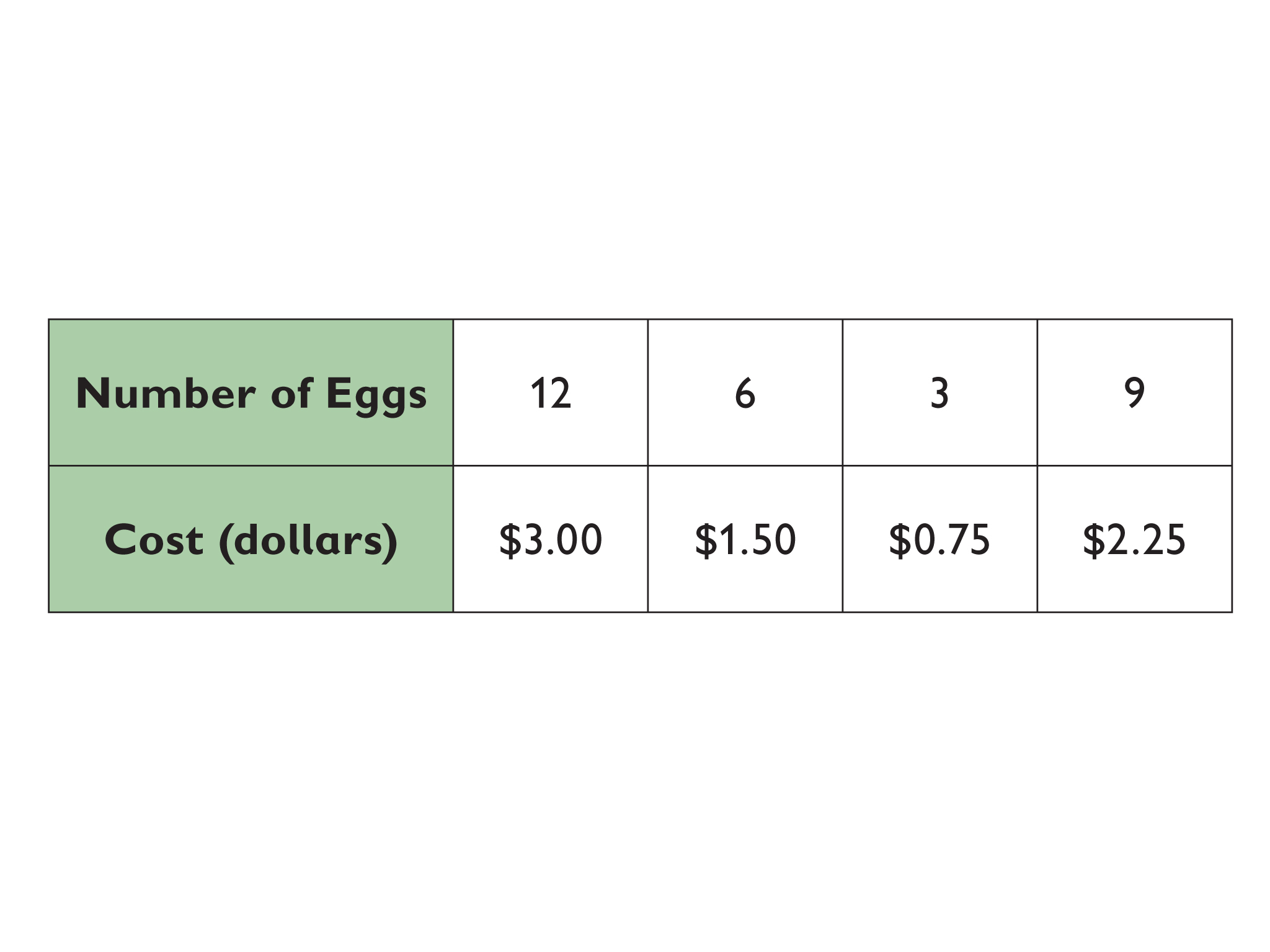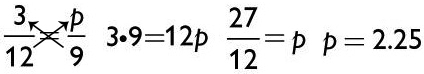- Author:
- Chris Adcock
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Exploring Rate In The Context Of Shopping

Overview
In this lesson, students explore rate in the context of grocery shopping. Students use the unit price, or price per egg, to find the price of any number of eggs.
Key Concepts
A unit price is a rate. The unit price tells the price of one unit of something (for example, one pound of cheese, one quart of milk, one box of paper clips, one package of cereal, and so on).
The unit price can be found by dividing the price in dollars by the number of units.
The unit price can be used to find the price of any quantity of something by multiplying the unit price by the quantity.
Goals and Learning Objectives
- Investigate rate as a unit price.
- Find a unit price by dividing the price in dollars by the number of units.
- Find the price of any quantity of something by multiplying that quantity by the unit price.
Breaking Eggs
Lesson Guide
Have students watch the video of a customer at the checkout stand of a grocery store. Discuss what happens and what information students are given in the video.
Tell students that today they will continue their investigation of rate by finding the price of 9 eggs. As they work on the problem, they should think about how to find the price of any quantity of eggs.
Opening
Breaking Eggs
Watch the video.
- What information do you know about this situation?
VIDEO: Broken Eggs
Math Mission
Lesson Guide
Discuss the Math Mission. Students will calculate the unit cost of an item and use this rate to find the price of any number of items.
Opening
Calculate the unit price of an item and use this rate to find the cost of any number of items.
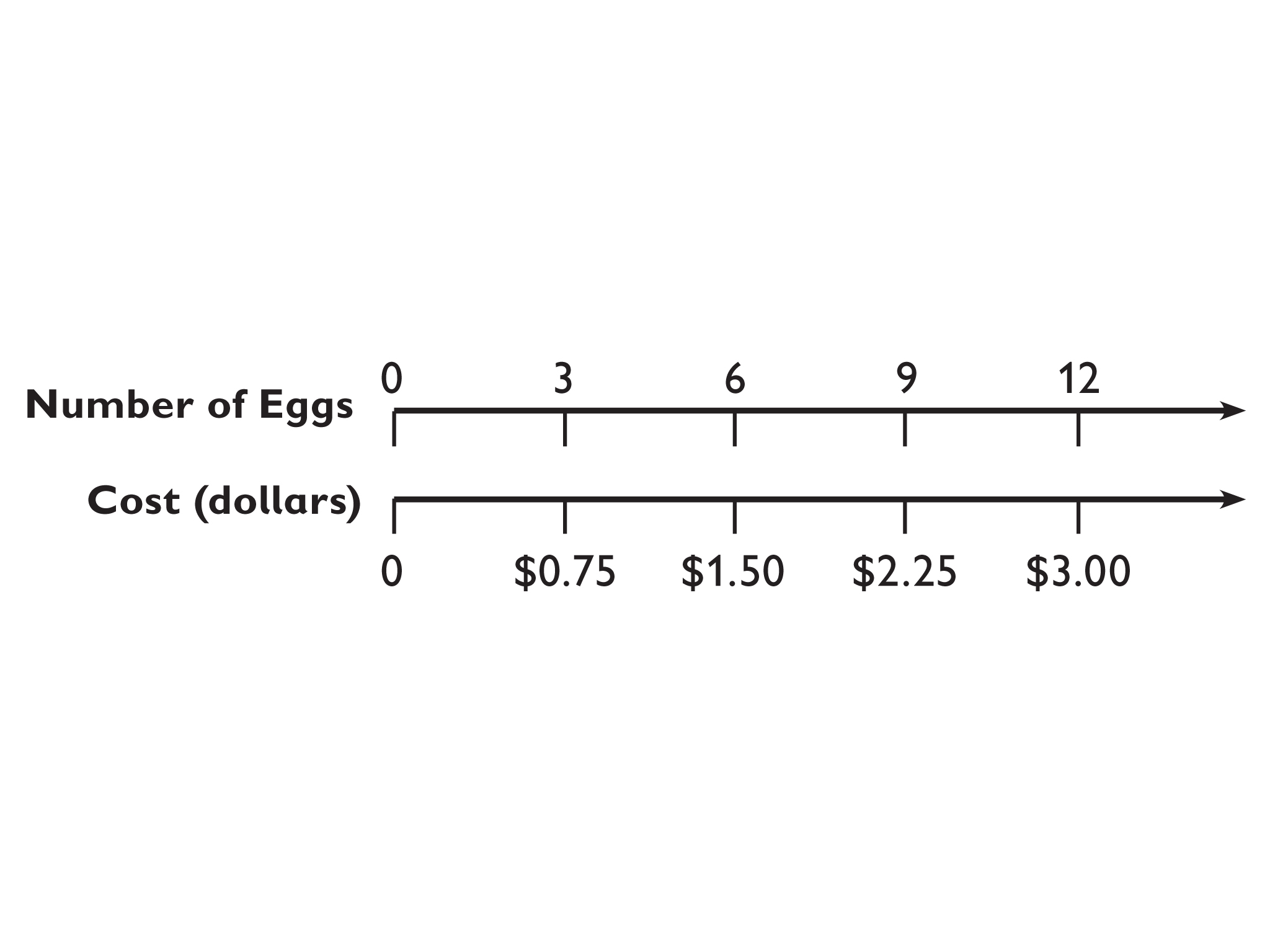
The Price of 9 Eggs
Lesson Guide
Let students use whatever calculation methods they want. Students can use a double number line, a table, or a calculator to solve the problem. It will be important to compare the different methods in Ways of Thinking.
ELL: When eliciting answers, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a foreign language. For example, if you hear a student saying the right things but using the wrong grammatical structure, show signs of agreement and softly rephrase using the correct grammar (using the student’s words as much as possible).
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- There are many different ways to find the price of 9 eggs. As students work, identify several students who are using different approaches to make sense of the problem. Be sure to identify at least one student who is using the unit price and multiplication.
Mathematical Practice 2: Reason abstractly and quantitatively.
- Identify students who can articulate what the different quantities in their solutions mean: what parts of the solution represent the price of 12 eggs, the price of 1 egg, and the price of 9 eggs?
Mathematical Practice 6: Attend to precision.
- Watch for students who show all the steps in their calculations and who calculate accurately and efficiently. Look for students who label their double number lines and complete their tables correctly using price in dollars and cents, and number of eggs. These students are attending to precision.
Interventions
Student has difficulty getting started.
- Describe the problem in your own words to your partner.
- What are you trying to find?
- What quantities do you see in the problem?
- Have you estimated the answer?
Student has an incorrect solution.
- Have you checked your work?
- Does your answer make sense?
- Explain the method you used to solve the problem.
Student has a solution.
- Why did you approach the problem in the way you did?
- Did you try a different method? Explain what you did.
- How does [Name]’s method compare with [Name]’s method? How are they similar? How are they different?
- Can you solve the problem using a different method? Explain the method.
Answer
- Nine eggs will cost $2.25.
Work Time
The Price of 9 Eggs
Carlos wants to buy 9 eggs.
- How much will the 9 eggs cost?
- Include in your solution:
- The quantities involved in the problem
- A diagram, table, double number line, or other representation that shows why your solution makes sense
- An equation, your work, and the solution
- A complete sentence that answers the question
- Remember that there are often multiple ways to solve a math problem. If you have time, try solving this in more than one way.
Hint:
- Do you think the price will be greater or less than the price of 12 eggs?
- How much would 1 egg cost?
- Does your answer make sense?
Prepare a Presentation
Prepare for Ways of Thinking
Look for students who find the rate by dividing and then use the rate to multiply. This is the preferred method because it allows students to find the price of any quantity of any item. If you have a student who uses this method, be sure to allow that student to present in Ways of Thinking. If no student uses this method, you should demonstrate it. Identify students who solve the problem using methods such as the following:
Table
Double Number Line
Fractions
Because 9 eggs is or of 12 eggs, the price is of $3.00.
⋅ $3.00 = $2.25
Cross Multiplication
Unit Price and Multiplication
Because $3.00 ÷ 12 = $0.25, the price of 1 egg is $0.25, so the price of 9 eggs is 9 × $0.25 = $2.25.
Unit Price and Repeated Addition
Because $3.00 ÷ 12 = $0.25, the price of 1 egg is $0.25, so the price of 9 eggs is $0.25 + $0.25 + $0.25 + $0.25 + $0.25 + $0.25 + $0.25 + $0.25 + $0.25 = $2.25.
Some students may find the unit price and then use repeated addition to find the price of 9 eggs. This approach does not exhibit grade level thinking.
Challenge Problem
Answers
- Paying $1.79 for a 32-ounce sports drink is a better buy than paying $0.83 for a 12-ounce sports drink.
- Explanations will vary.
Work Time
Prepare a Presentation
- Explain how you determined the cost of 9 eggs.
- Use your work to support your explanation.
Challenge Problem
- Which is a better buy: $1.79 for 32 ounces of a sports drink, or $0.83 for 12 ounces of the same sports drink?
- Explain your thinking.
Make Connections
Lesson Guide
By the end of the discussion, students should understand one another’s methods and make connections between the methods.
Select a variety of work and connect the different representations. Display all of these approaches:
- Tables
- Double number lines
- Calculations that find only the price of 9 eggs (for example, by cross multiplying)
- Calculations that find the unit price and then use it to find the price of 9 eggs
By the end of this discussion, students should understand that unit price is a rate and the grade level way to solve this problem is to find the unit rate and then multiply by the number of times that unit rate is applied.
Move back and forth among the representations, and encourage students to critique each method. Focus on the mathematics by asking questions such as the following:
- How did [Names] make sense of the problem?
- How was the egg problem solved differently?
- What was similar about the approaches?
- What was different?
- Where do you see the unit price in the different solution methods? Where do you see the price of 9 eggs?
- Which approach showed the structure of the mathematics most clearly?
- Can you find the price of 11 eggs? Which approach would you use? Explain why.
ELL: When giving directions for this discussion, be sure that students understand that they can complement their oral explanation with graphs, pictures, and drawings. Provide a few sentence frames that you think might be needed for ELLs.
SWD: As students present their solutions, make connections between different solutions to the same problem so that students can see the multiple ways to solve a problem.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ approaches to solving the problem.
- Determine an approach you will use to solve a different problem involving unit price.
Hint:
As your classmates present, ask questions such as:
- What are the quantities in this situation?
- What equation did you use?
- Where do you see the price of 1 egg in your equation?
- What operation did you use to find the unit price? Explain your thinking.
- Does your answer make sense? Why?
- If you know the unit price, how do you find the price for any amount of eggs?
- You used an equation and another student used a table to find the cost of 9 eggs. Can you compare the two representations?
Find the Unit Price
Lesson Guide
Let students use whatever calculation methods they want. Students can use a double number line, a table, or a calculator to solve the problem.
Interventions
Student has difficulty getting started.
- Describe the problem in your own words to your partner.
- What are you trying to find?
- What quantities do you see in the problem?
- Have you estimated the answer?
Student has an incorrect solution.
- Have you checked your work?
- Does your answer make sense?
- Explain the method you used to solve the problem.
Student has a solution.
- Why did you approach the problem in the way you did?
- Can you solve the problem using a different method? Explain the method.
Answer
- Apples cost $2.50 per pound. $2.50 per pound is the unit price—it is the price of 1 pound.
Work Time
Find the Unit Price
Emma buys 3 pounds of apples for $7.50.
- What is the unit price of the apples?
Hint:
- What are the two quantities in this problem?
- How can you find the cost of 1 pound of apples?
- What operations would you use?
- Does your answer make sense?
Find the Cost
Lesson Guide
Let students use whatever calculation methods they want. Students can use a double number line, a table, or a calculator to solve the problem.
Interventions
Student has difficulty getting started.
- Describe the problem in your own words to your partner.
- What are you trying to find?
- What quantities do you see in the problem?
- Have you estimated the answer?
Student has an incorrect solution.
- Have you checked your work?
- Does your answer make sense?
- Explain the method you used to solve the problem.
Student has a solution.
- Why did you approach the problem in the way you did?
- Can you solve the problem using a different method? Explain the method.
Answer
- The unit price of apples is $2.50 per pound. If you want to find the cost of 7 pounds of apples, you need to multiply 7 times $2.50. Thus, 7 pounds of apples cost $17.50.
Work Time
Find the Cost
Emma changes her mind. Instead of buying 3 pounds of apples for $7.50, she buys 7 pounds.
- How much money will she pay for the apples?
Hint:
Once you know what 1 pound of apples costs, how can you find the cost of 7 pounds?
Comparing Prices
Lesson Guide
Let students use whatever calculation methods they want. Students can use a double number line, a table, or a calculator to solve the problem.
Interventions
Student has difficulty getting started.
- Describe the problem in your own words to your partner.
- What are you trying to find?
- What quantities do you see in the problem?
- Have you estimated the answer?
Student has an incorrect solution.
- Have you checked your work?
- Does your answer make sense?
- Explain the method you used to solve the problem.
Student has a solution.
- Why did you approach the problem in the way you did?
- Can you solve the problem using a different method? Explain the method.
Answers
- They both paid the same amount per ounce. Carlos paid , or $0.25 per ounce. Emma paid , or $0.25 per ounce.
Work Time
Comparing Prices
Carlos bought a box of cereal. The box contained 16 ounces of cereal and cost him $4.00.
Emma bought a box of a similar cereal. The box contained 24 ounces of cereal and cost her $6.00.
- Who got the better deal? Explain how you know.
Hint:
- What are the two quantities in this problem?
- How can you find the cost of 1 ounce?
- What operations should you use?
- Does your answer make sense?
Understanding Unit Price
Lesson Guide
Discuss the summary with students. Ask students to come up with further examples of unit price.
Formative Assessment
Summary of the Math: Understanding Unit Price
Read and Discuss
- The unit price is a rate that tells you the price of 1 unit of something—for example, the price of 1 pound of cheese, 1 quart of milk, 1 box of paper clips, 1 package of cereal, and so on.
- The unit price, or rate, can be found by dividing the price in dollars by the number of units.
- The unit price can be used to find the price of any quantity by multiplying the unit price by the quantity.
Hint:
Can you:
- Explain what unit price means and how to find it?
- Include the term rate ?
- Explain how to find the total price of an item by using its unit price?
Reflect On Your Work
Lesson Guide
Students write a reflection on their work. Students may use the sentence starter below if they find it helpful.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
As I worked on unit price problems, I found that a useful strategy is …