Rules For Computing A Value

Overview
In this lesson, students use their knowledge of rates, graphs of rates, and formulas to solve problems.
Key Concepts
The formula for a rate is a mathematical way of writing a rule for computing a value. Rate formulas describe a constant relationship between two quantities. Each point on the graph of a rate shows a pair of related values. A graph of a constant rate is a straight line.
Goals for Learning Objectives
- Uncover any partial understandings and misconceptions students have about rate, graphs of rates, and formulas.
- Develop a more robust understanding of rate.
- Help identify which Gallery problems students should work on.
Revise and Extend Your Work
Lesson Guide
Have students work in pairs to revise their Self Check. Encourage students to incorporate ideas from their partner in their revisions.
By now, students have worked with graphs and rate formulas for a while. Students will have varying degrees of understanding of graphs and formulas, and in many cases, their understanding is still very delicate, containing a mix of good conceptualization, partial understandings, and misconceptions.
This pre-assessment should uncover any partial understandings and misconceptions. Students' revised work will provide data that you and your students can use to assess the degree to which they were able to cement their understanding of rate graphs and formulas.
Answers
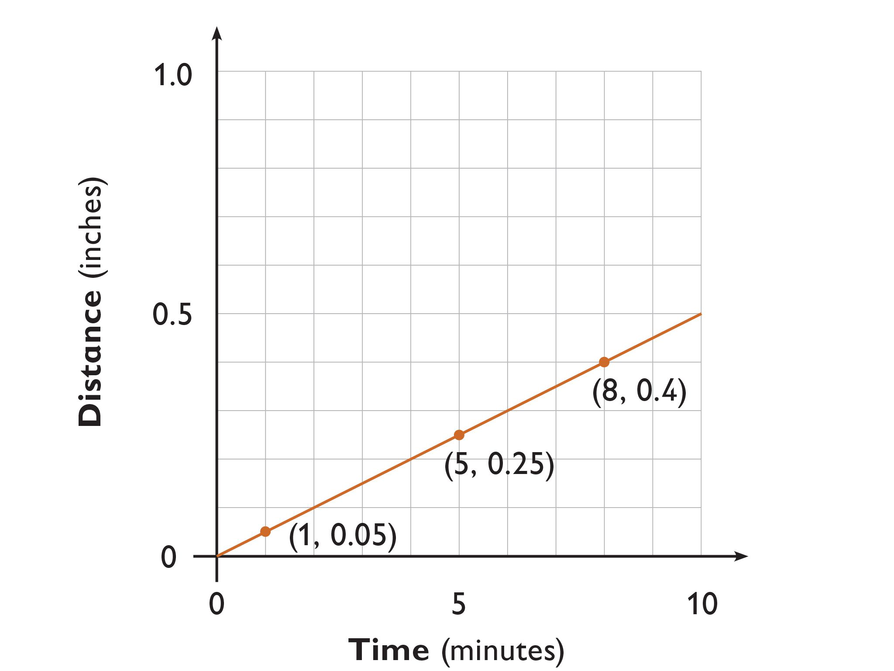
- The graph most likely shows the speed of a garden snail.
- In 8 minutes, the creature traveled 0.4 inch.
- In 3 minutes, the creature traveled 0.15 inch.
- The creature's rate of speed is 0.05 inch per minute.
- In 12 minutes, the creature travels 0.6 inch.
- . It takes the creature 40 minutes to travel 2 inches.
Opening
Check Your Understanding
Use the graph to answer the questions.
- Does this graph most likely show the speed of a garden snail or a cheetah?
- How far did this creature travel in 8 minutes?
- How far did this creature travel in 3 minutes?
- What is this creature’s rate of speed in inches per minute?
- Solve an equation to find the distance the creature travels in 12 minutes.
- Solve an equation to find the time it takes the creature to travel 2 inches.
Independent and Dependent
Lesson Guide
Discuss the idea of independent variables and dependent variables.
The work students do in this lesson and in revising their pre-assessments will help you and your students make decisions about the work they will undertake during the Gallery lesson. Students' work in this lesson will reveal the depth and clarity of their understanding of the connections among rates, graphs of rates, and formulas.
Students whose understanding of rate is still delicate should turn first to the exercises and then to application problems.
Students who successfully revise their pre-assessments and who feel fairly confident in their understanding of rate should choose from any of the application and the problem-solving problems.
Students who feel that they have a robust understanding of rate may choose from any of the problem-solving or the deeper mathematics problems.
SWD: Consider the prerequisite skills for this Putting it Together lesson. Students with disabilities may need direct instruction and/or guided practice with the skills needed to complete the tasks in this lesson. It may be helpful to pull individual students and/or a small group for direct instruction or guided practice with the skills they have learned thus far in this unit.
Opening
Independent and Dependent
Read and Discuss
- You’ve seen many quantitative relationships—for example, the relationship between distance and time when you’re riding your bike. In these relationships, the quantity that changes independently is called the independent variable, and the quantity that is calculated is called the dependent variable.
- In the above relationship, distance is the dependent variable because your distance depends on the amount of time that has passed. Time is the independent variable because the amount of time that has passed really does not depend on how far you have gone.
- You graph the independent variable on the horizontal axis, the x-axis, and the dependent variable on the vertical axis, the y-axis. There isn’t any great mystery behind this; it’s just something mathematicians and scientists agreed on so that everyone would graph things the same way.
Math Mission
Lesson Guide
Discuss the Math Mission. Students summarize what they know about using rates, graphs of rates, and formulas.
Opening
Summarize what you know about using rates, graphs of rates, and formulas.
Cost Versus Weight
Lesson Guide
Have students work on their graphs and problems individually. When they are done, have students share their problems with a partner. Partners should use the graphs to answer the problems.
As students work, pay attention to how they are finding the values for their graphs. The different approaches you notice will allow you to engage students in a rich conversation during Ways of Thinking.
Look for students who:
- Plot only one point and draw the graph through that point and the origin.
- Have calculation errors that lead to graphing errors.
- Have graphing errors caused by using the inverse rate.
SWD: Consider the prerequisite skills for this Putting it Together lesson. Students with disabilities may need direct instruction and/or guided practice with the skills needed to complete the tasks in this lesson. It may be helpful to pull individual students and/or a small group for direct instruction or guided practice with the skills they have learned thus far in this unit.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Select a variety of problems that ask for different unknowns. For example, in the formula c = 0.4w, the cost is known and the weight is unknown, or the weight is known and the cost is unknown. Students can make sense of the problem in different ways.
Mathematical Practice 4: Model with mathematics.
- Watch for how students determine what values to plot on graphs. Some students may make a table of values, easily translating from one model (formula) to another model (table) to the final model (graph). These students are modeling the mathematics in different ways.
Mathematical Practice 6: Attend to precision.
- Watch for students who attend to different levels of precision. For example, look for students who plot each pair of values and then draw the graph through all the points.
Interventions
Student has difficulty getting started.
- What is the rate that is represented by the formula?
- How can you graph that rate?
Student has an incorrect solution.
- Could your partner use your graph to answer the problem? What happened?
- Explain how you used the formula to make a graph.
- Explain how you used the graph to write your problem.
Student has a solution.
- Where do you see the rate on your graph? In your formula?
- What does a point on your graph represent?
- What strategy did you use to write a problem for your graph?
- Where do you see the known quantity on your graph? Where do you see the answer?
Answers
- Word problems will vary. Sample answer: In 2005, Marisol paid $2.00 for a silver ring that weighs 5 grams. What was the price per gram?
- The independent variable is weight.
- Student discussions will vary.
- Problem answers will vary.
Work Time
Cost Versus Weight
- Graph the formula c = 0.4w. Label the x-axis “weight” and the y-axis “cost.”
- Write a problem using the information from the graph.
- What is the independent variable in your problem?
- Share your problem with a partner. Discuss whether your partner agrees that your problem can be answered using the information from the graph.
- Challenge your partner to use the graph to answer your problem.
Hint:
For an idea for a word problem, look at the exercises from Lesson 2 that had to do with price.
Volume Versus Time
Lesson Guide
Have students work on their graphs and problems individually. When they are done, have students share their problems with a partner. Partners should use the graphs to answer the problems.
Interventions
Student has difficulty getting started.
- What is the rate that is represented by the formula?
- How can you graph that rate?
Student has an incorrect solution.
- Could your partner use your graph to answer the problem? What happened?
- Explain how you used the formula to make a graph.
- Explain how you used the graph to write your problem.
Student has a solution.
- Where do you see the rate on your graph? In your formula?
- What does a point on your graph represent?
- What strategy did you use to write a problem for your graph?
- Where do you see the known quantity on your graph? Where do you see the answer?
Answers
- Word problems will vary. Sample answer: A gasoline pump delivers 4 gallons of gas per minute. How many minutes will it take to pump 12 gallons of gas?
- The independent variable is time.
- Student discussions will vary.
- Problem answers will vary.
Work Time
Volume Versus Time
- Graph the formula v = 4t. Label the x-axis “time” and the y-axis “volume.”
- Write a problem using the information from the graph.
- What is the independent variable in your problem?
- Share your problem with a partner. Discuss whether your partner agrees that your problem can be answered using the information from the graph.
- Challenge your partner to use the graph to answer your problem.
Distance Versus Time
Lesson Guide
Have students work on their graphs and problems individually. When they are done, have students share their problems with a partner. Partners should use the graphs to answer the problems.
Interventions
Student has difficulty getting started.
- What is the rate that is represented by the formula?
- How can you graph that rate?
Student has an incorrect solution.
- Could your partner use your graph to answer the problem? What happened?
- Explain how you used the formula to make a graph.
- Explain how you used the graph to write your problem.
Student has a solution.
- Where do you see the rate on your graph? In your formula?
- What does a point on your graph represent?
- What strategy did you use to write a problem for your graph?
- Where do you see the known quantity on your graph? Where do you see the answer?
Answers
- Word problems will vary. Sample answer: Emma's aunt drove her car on a 70-mile scenic drive. It took her 2 hours from start to finish. What was her average speed for the drive?
- The independent variable is time.
- Student discussions will vary.
- Problem answers will vary.
Challenge Problem
Answers
- Problems, graphs, and solutions will vary.
Work Time
Distance Versus Time
- Graph the formula d = 35t. Label the x-axis “time” and the y-axis “distance.”
- Write a problem using the information from the graph.
- What is the independent variable in your problem?
- Share your problem with a partner. Discuss whether your partner agrees that your problem can be answered using the information from the graph.
- Challenge your partner to use the graph to answer your problem.
Challenge Problem
- Write a problem that requires making and using information from graphs to find solutions, similar to the problems you just worked on.
- Set up the problem with a blank graph, and trade problems with a partner.
- Make the graph and solve your partner’s problem.
Make Connections
Lesson Guide
Students should understand each other's methods and make connections between methods. By the end of the discussion, all students should understand that any rate can be graphed, and they should see the connections between graphs and formulas.
Mathematics
Encourage students to critique each other's work. Ask questions such as the following:
- How did you use the formula to make a graph?
- Did someone use a different method? What did you do?
- Where do you see the rate in the formula? On the graph?
- How does [student name]'s graph compare with [student name]'s graph?
- What is similar?
- What is different?
- Which graph is easiest to read?
- Compare one student's problem with another student's problem.
- How are the problems similar?
- How are they different?
- How can you use the related graph to solve the problem?
- What strategy did you use to make sense of your partner's word problem?
- Did anyone use a different strategy? Explain what you did.
- If you graph any rate formula, do you think it will be a straight line? Why or why not?
- How did you know what was the independent variable and the dependent variable?
Performance Task
Ways of Thinking: Make Connections
Take notes as you listen to problems your classmates wrote to match the formula and the graph.
Hint:
As your classmates present, ask questions such as:
- How did you use the formula to make a graph?
- Where do you see the rate in the formula? On the graph?
- What strategy did you use to make sense of your partner’s word problem?
- If you graph any rate formula, do you think it will be a straight line? Why or why not?
Summarize Your Learning
A Possible Summary
Rate compares two quantities and expresses the comparison as a new quantity using the word “per.” You can use a rate formula to create a graph. Each point on the graph shows a pair of related values. A graph of a constant rate is a straight line.
Additional Discussion Points
- The formula for a rate is a mathematical way of writing a rule for computing a value.
- Rate formulas describe a constant relationship between two quantities.
- Each point on the graph of a rate shows a pair of related values. A graph of a constant rate is a straight line.
- The dependent variable depends on the input of the independent variable.
Formative Assessment
Summary of the Math: Summarize Your Learning
Take a moment to summarize the concept of rate.
Hint:
Check your summary.
- Does your summary explain how to represent quantitative relationships involving rates using graphs and formulas?
- Does your summary talk about how to create one such representation given another?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections. If any reflections look interesting enough to pursue later, put them in a canvas and “collaborate” to share the canvas with the class.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
The most important thing I learned about rates and quantitative relationships in this unit is…