Reviewing Quantitative Relationships

Overview
In this lesson, students represent quantitative relationships involving rates using tables, graphs, double number lines, and formulas. Students will understand how to create one such representation when given another representation.
Key Concepts
Quantitative relationships involving rates can be represented using tables, graphs, double number lines, and formulas. One such representation can be used to create another representation. Two rates can describe each situation: the rate and its inverse. For the water pump situation, there are two related formulas: a formula for finding the quantity of water pumped for any amount of time, and a formula for finding the amount of time for any quantity of water.
Goals and Learning Objectives
- Understand that tables, graphs, double number lines, and formulas can be used to represent the same situation.
- Compare the different representations within a situation and the same representation across similar situations.
- Understand each representation and how to find the rate in each one.
Graph of Pumping Water
Lesson Guide
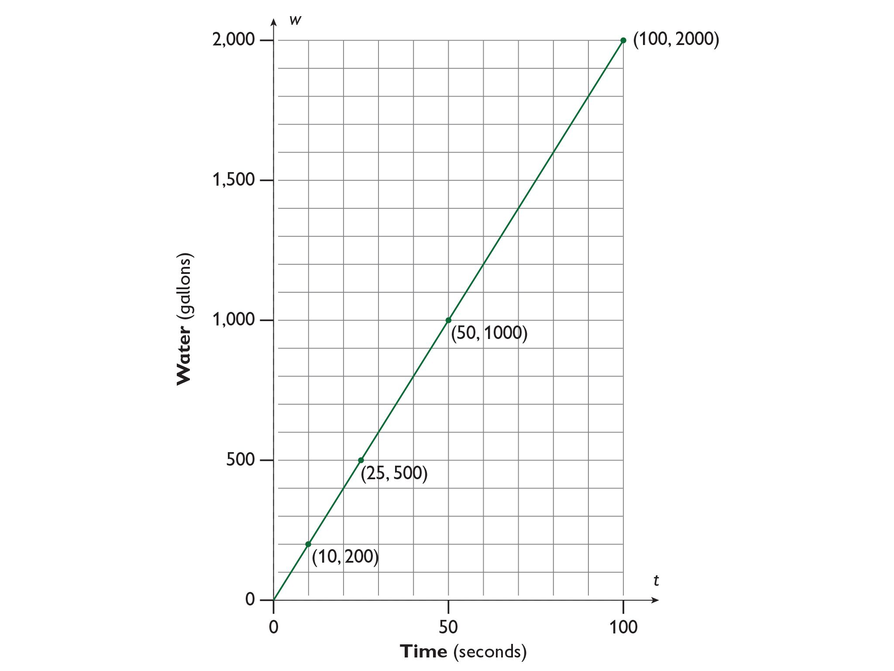
Review the graph and make sure students know how to read the coordinates and interpret the graph.
- The point (10,200) tells you 200 gallons were pumped in 10 seconds.
- The rate is 20 gallons/second.
Opening
Graph of Pumping Water
The graph shows the amount of water pumped over time.
- What does the point (10, 200) tell you?
- At what rate is the water being pumped?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will represent quantitative relationships in different ways.
SWD: Students with disabilities may struggle to independently find patterns and to observe similarities between formulas. Use your understanding of your students' needs to inform any pre-teaching and/or interventions you may provide.
Opening
Represent rates in different ways.
Graph the Relationships
Lesson Guide
As students work, look for these types of responses:
- Students that find the rate by solving for gallons per minute.
- Students that find the rate by solving for minutes per gallon.
- Students who use different types of formulas for the situations, because the inconsistency will cause problems when graphing.
SWD: Color coding of ideas, relationships, and formulas can be helpful for students with special needs. Consider providing these color-coded formulas to students once they have learned about the concepts.
Mathematical Practices
Mathematical Practice 6: Attend to precision; and Mathematical Practice 1: Make sense of problems and persevere in solving them.
- To find each rate and formula, students must first make sense of the problem situation and attend to precision. In some situations, the rate is given, and students need to write the formula. In other situations, students need to calculate the rate. In some situations, the time is given first and then the number of gallons. In other situations, the number of gallons is given first and then the time.
- Later, students will compare the different situations on the same graph. While graphing, students may have difficulty selecting axes value ranges that will work for all four situations. Identify student work that has different values for the axes and that attends to different levels of precision.
Mathematical Practice 4: Model with mathematics.
- Students will be working from one model in order to create another model of the same situation (for example, from a table to a formula to a graph). Watch for students who are able to model the mathematical relationships correctly.
- Also look for students who are able to use their graph to draw conclusions about the four situations.
Interventions
Student is having difficulty getting started.
- Describe what you need to do for each situation to your partner.
- What information do you know?
- What is the first thing you need to find?
- Once you identify the rate, what will you do?
- How can you use your formula to make a graph of the situation?
Student doesn't understand how to write a formula.
- How do you know your formula is correct?
- What do the variables in your formula represent?
- What formula matches this line on the graph? Explain how you know.
- How does your formula compare to your partner's formula?
- How are they the same?
- How are they different?
- Can you use both formulas to make the same graph?
Make sure your students are correctly representing the units.
- What does the vertical axis of your graph show? What is the scale? What size intervals did you use?
- What does the horizontal axis of your graph show? What is the scale? What size intervals did you use?
- Does the range of your scales cover all problem situations?
Answers
- Students should come up with the same formulas, but they might use different variables for gallons, g, or time, t. Solving for gallons:
- Pump 1: g = 125t
- Pump 2: g = 52t
- Pump 3: g = 260t
- Pump 4: g = 52t
- Solving for minutes:
- Pump 1: t = (1,125)g
- Pump 2: t = (152)g
- Pump 3: t = (1,260)g
- Pump 4: t = (152)g
Work Time
Graph the Relationships
Below are four situations describing the rate of water flowing through a pump.
Situation 1: Pump 1 pumps water at a rate of 125 gallons per minute.
Situation 2: Pump 2 pumps water at a constant rate. Pump 2 pumps 364 gallons in 7 minutes.
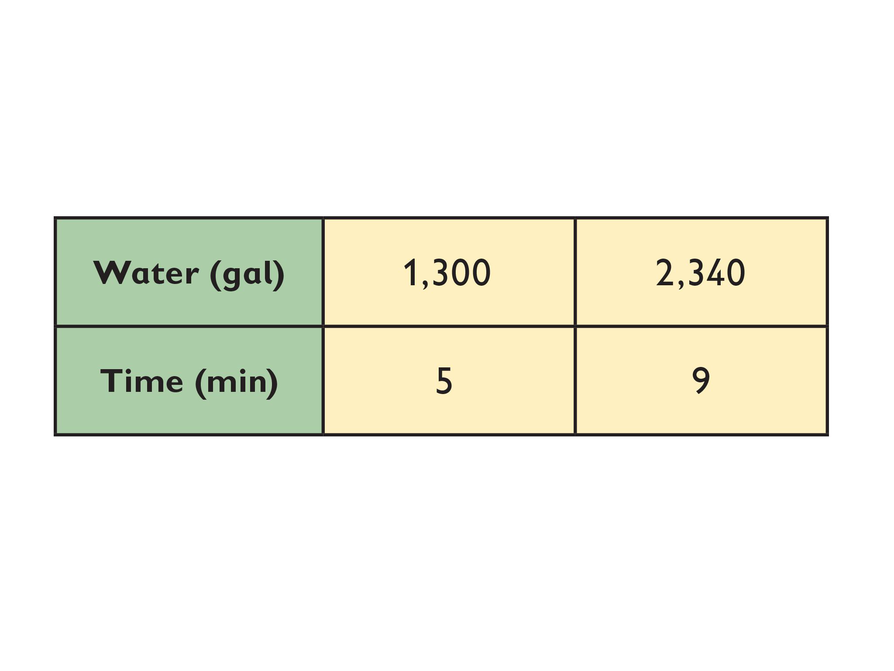
Situation 3: Pump 3 pumps at a constant rate, represented by the table.
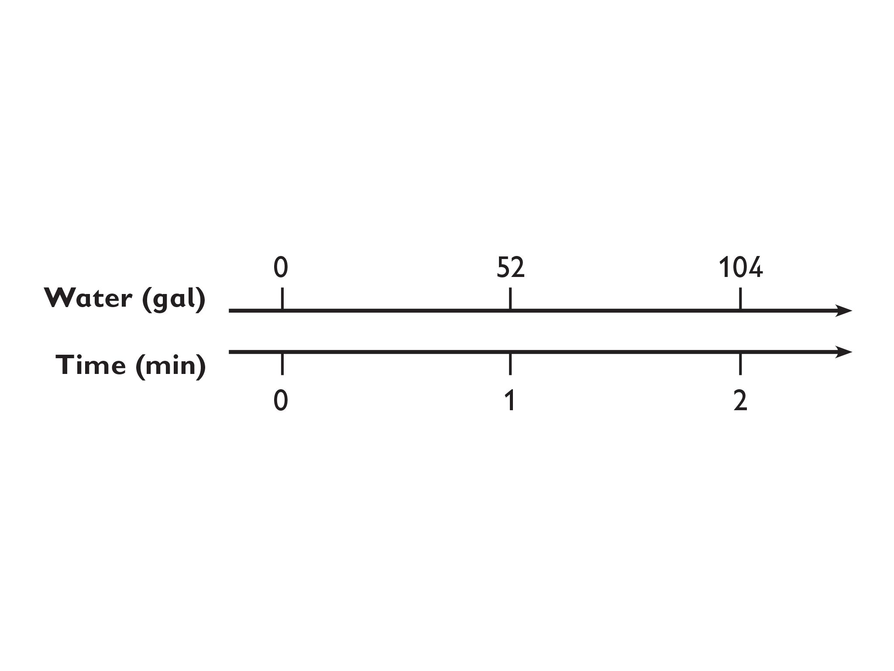
Situation 4: Pump 4 pumps at a constant rate, represented by the double number line.
For each situation, do the following.
- Write a formula that represents the rate relationship.
- Graph all four relationships on a single graph.
Situation 3:
Situation 4:
Hint:
- What rate will you find gallons per minute or minutes per gallon?
- How will you represent this rate as a formula?
- Why should you represent time on the x -axis?
Prepare a Presentation
Preparing for Ways of Thinking
- Look for students who wrote equations that solve for gallons, in particular students whose methods may differ from others.
- Look for students who wrote equations that solve for minutes, in particular students whose methods may differ from the others.
- Look for students who had issues with graphing due to the formula they wrote.
- Look for students who have a clear understanding of the relationship between rate and the slope of the graph.
Challenge Problem
Answers
- On the graph, the line for pump 3 is the steepest because it is pumping water at the fastest rate.
- Pump 1: g = 125t or
- Pump 2: g = 52t or
- Pump 3: g = 260t or
- Pump 4: g = 52t or
- Possible answer: We are interested in how many gallons of water there will be after a given time, so the number of gallons depends on the time. Thus, time is the independent variable and gallons is the dependent variable. The formula g = kt indicates that time is the independent variable and g is the dependent variable. The formula t = kg indicates that volume is the independent variable and time is the dependent variable.
Work Time
Prepare a Presentation
Prepare a presentation about the four situations.
- Compare the situations. What is similar, and what is different?
- What did you notice about two of the situations?
Challenge Problem
- Which line on your graph of the rate relationships is the steepest? Explain why.
- In this problem, the time is considered the independent variable and the volume the dependent variable. Explain why.
Make Connections
Lesson Guide
By the end of the discussion, students should understand each others' methods and make connections between methods.
If any students work on the challenge problems, have them share their thinking about independent and dependent variables.
ELL: When discussing how to find the formulas, make it a point to write, in words, what each of the formulas represents. It is important to provide students with the opportunity to practice a combination of written and oral skills.
Mathematics
Make note of any mathematical practices that you observe students using.
Ask the following questions:
- How does one student's graph compare with another student's graph?
- What is similar?
- What is different?
- Which graph is easiest to read?
- Did anyone use different strategies? Explain what you did.
- Where do you see the rate in each representation (table, double number line, graph, formula)?
- Which representation of the rate situation is easiest for you to understand? Why?
- What conclusions can you draw from interpreting the graph?
- Which pump is the fastest? How do you know?
- Which pump is the slowest? How do you know?
- How does the graph show that each pump works at a constant rate?
Performance Task
Ways of Thinking: Make Connections
Take notes as you listen to your classmates’ solutions.
Hint:
As your classmates present, ask questions such as the following:
- What strategies did you use to make sense of the four situations?
- Whose method makes most sense to you? Why?
- Where do you see the rate in each representation (table, double number line, graph, formula)?
- Which representation of the rate situation is easiest for you to understand? Why?
- What conclusions can you draw from interpreting the graph?
- Which pump is the fastest? How do you know?
- Which pump is the slowest? How do you know?
- How does the graph show that each pump works at a constant rate?
Summarize Your Learning
A Possible Summary
You can represent rate situations using tables, double number lines, graphs, or formulas. You can use one representation to create another representation.
Additional Discussion Points
- Quantitative relationships involving rates can be represented using tables, graphs, double number lines, and formulas. One such representation can be used to create another representation.
- Two rates can describe each situation: each rate is the inverse of the other.
- For the water pump situation, there are two related formulas: a formula for finding the quantity of water pumped for any amount of time and a formula for finding the amount of time for any quantity of water.
Formative Assessment
Summary of the Math: Summarize Your Learning
Summarize the mathematics you learned about graphing rates.
Hint:
Check your summary.
- Does your summary explain what each point on your graph represents?
- Does your summary include the term constant rate ?
- Does your summary describe the two rates for each situation and their related formulas?
Check Your Understanding
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery problems and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes about what their work reveals about their current levels of understanding and their different problem-solving approaches. Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
ELL: It might be helpful for ELLs and other students to have a sample or model for the concepts, strategies, and applications that will be addressed in the quiz and the format you want them to follow. Be prepared to address and explicitly re-teach or review vocabulary, concepts, strategies, and applications.
SWD: Students with disabilities may benefit from having the Self Check presented in a variety of ways (as auditory and visual information). Provide students the option of listening to the content for this task. Some students with disabilities may need additional time to complete the Self Check. Be sure to make provisions for the additional time or consider reducing the number of tasks required for students to demonstrate mastery of skill.
Interventions
Student has trouble getting started
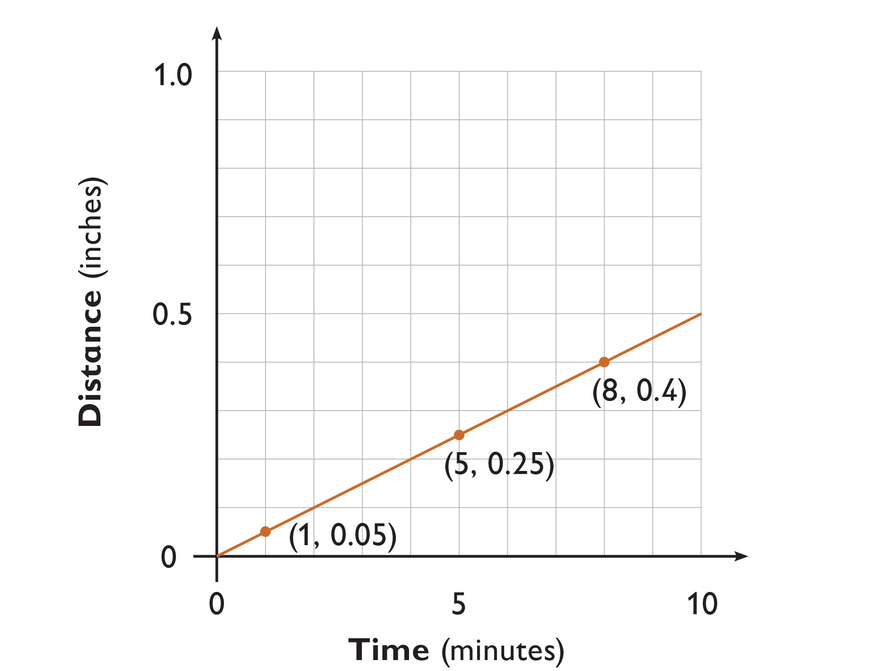
- The scale of the graph is in inches; which animal is more likely to travel just one inch at a time?
Student does not know how to write a formula.
- Look at the formulas you wrote in the previous lessons. How do those formulas relate to this situation?
- What is the general formula to find distance? How can you use this to help you write the formula for this situation?
- What is the general formula to find time? How can you use this to help you write the formula for this situation?
Answers
- The graph most likely shows the speed of a garden snail.
- In 8 minutes, the creature traveled 0.4 inch.
- In 3 minutes, the creature traveled 0.15 inch.
- The creature's rate of speed is 0.05 inch per minute.
- In 12 minutes, the creature travels 0.6 inch.
- . It takes the creature 40 minutes to travel 2 inches.
Formative Assessment
Check Your Understanding
Use the graph to answer the questions.
- Does this graph most likely show the speed of a garden snail or a cheetah?
- How far did this creature travel in 8 minutes?
- How far did this creature travel in 3 minutes?
- What is this creature’s rate of speed in inches per minute?
- Solve an equation to find the distance the creature travels in 12 minutes.
- Solve an equation to find the time it takes the creature to travel 2 inches.
Reflect On Your Work
Lesson Guide
Have each student do a quick reflection before the end of class. Review the reflections.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One thing I know about representing rate relationships is …