- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Dollars and Pesos
Hours, Speed, and Miles
Prepare a Presentation
Price per Gallon
Stack of Books
Using Rates To Solve Problems

Overview
Students use their knowledge of rates to solve problems.
Key Concepts
Given any two values in a rate situation, you can find the third value.
These three equations are equivalent, and they all describe rate relationships:
y = rx, r = yx, x = yr
At the beginning of this lesson (or for homework), students will revise their work on the pre-assessment Self Check. Their revised work will provide data that you and your students can use to reassess students' understanding of rate. You can use this information to clear up any remaining misconceptions and to help students integrate their learning from the past several days into a deeper and more coherent whole.
The work students do in this lesson and in revising their pre-assessments will help you and your students decide how to help them during the Gallery. In this lesson, students will reveal the depth and clarity of their understanding of rate.
- Students whose understanding of rate is still delicate should get extra help during the Gallery.
- Students who feel that they have a robust understanding of rate may choose from any of the problem-solving or deeper mathematics problems in the Gallery.
Goals and Learning Objectives
- Uncover any partial understandings and misconceptions about rate.
- Develop a more robust understanding of rate.
- Identify which Gallery problems to work on.
Revise and Extend Your Work
Lesson Guide
Have students work in pairs to revise their work from the Self Check. Encourage students to incorporate ideas from their partner in their revisions. Then students will work together on a similar task.
Students have worked with rate in a variety of contexts. At this point, their understanding is still very delicate, containing a mix of good conceptualization, partial conceptions, and some misconceptions.
While students work with their partners, note different approaches to the task:
- How do they organize their work?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
Answers
- He can multiply the rate $3.00 per pound by 5.75 pounds to find the price in dollars.
- She can divide 12 miles by 1.5 hours to find her speed in miles per hour.
- He can divide 325 square feet of wall by 85 square feet per quart to find the number of quarts.
- She can divide 13.1 miles by 2.6 hours to find her speed in miles per hour.
Opening
Revise and Extend Your Work
Work with your partner to revise your work on the Self Check.
- Explain what calculation the person can perform to find what he or she wants to know.
- Explain what the unit of the answer is.
- At the store, Jason sees that the price of cherries is $3.00 per pound. What calculation can he perform to find the price of 5.75 pounds of cherries?
- Rosa knows that she can skate to the park in 1.5 hours. The park is 12 miles away. What calculation can she perform to find her speed?
- Denzel knows that 1 quart of paint will cover about 85 square feet of wall. He needs enough paint to cover 325 square feet of wall. What calculation can Denzel perform to find how many quarts of paint he will need?
- Mina ran a half marathon (13.1 miles) this weekend. She completed the run in 2.6 hours. What calculation can Mina perform to find her speed during this run?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will work through several rate problems using what they have learned about rates.
Opening
Use what you know about rates to work through problems.
Distance, Time, and Speed
Lesson Guide
Pay attention to how students are finding values for their tables. Do they start with the first row? With some other row? How are students navigating between the rows?
The different approaches you notice will allow you to engage students in a rich conversation during Ways of Thinking.
SWD: Consider the prerequisite skills for this Putting it Together lesson. Students with disabilities may need direct instruction and/or guided practice with the skills needed to complete the tasks in this lesson. It may be helpful to pull individual students and/or a small group for direct instruction or guided practice with the skills they have learned thus far in this unit.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- In these problems, students can enter any numbers into the tables as long as the relationship between the numbers is correct. As students work, identify a variety of work with an eye to making connections among different methods. For example, look for the following different approaches:
- Choosing a speed and a time, and then calculating distance; choosing a distance and a time, and then calculating speed; and choosing a speed and a distance, and then calculating time.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Look for students who understand that they can choose any two numbers to find the third number; these students are using a general method to solve all rate problems.
Interventions
Student has difficulty connecting the problem to familiar situations.
- What do you think a typical bike riding speed might be?
- How long might you ride your bike? If you ride for that length of time at that speed, how far would you ride?
- What is the relationship among speed, distance, and time?
- What is a common rate for the speed of a car?
- If a car travels for two hours, how far would it go at that constant speed?
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
- Answers will vary, but the relationships should show that speed is equal to distance divided by the time.
Work Time
Distance, Time, and Speed
In this problem, you will work with three quantities: distance, time, and speed.
Create a set of three numbers that shows the relationship among the quantities. For instance, if you chose a time of 3 hours and a speed of 25 miles per hour, the distance would be 75 miles.
- Create your sets of three numbers in three different ways:
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
INTERACTIVE: Distance, Time, and Speed
Price per Gallon
Lesson Guide
Students will fill in a table showing the relationship between gallons, total price, and price per gallon.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students can enter any numbers into the tables as long as the relationship between the numbers is correct. As students work, identify a variety of work with an eye to making connections among different methods. For example, look for the following different approaches:
- Choosing a number of gallons and a total price, and then calculating unit price; choosing a total price and a unit price, and then calculating a number of gallons; and choosing a number of gallons and a unit price, and then calculating total price.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Look for students who understand that they can choose any two numbers to find the third number; these students are using a general method to solve all rate problems.
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
- Answers will vary, but the relationships should show that price per gallon is equal to price divided by gallons.
Work Time
Price per Gallon
In this problem, you will work with three quantities: gallons, total price, and price per gallon.
Create a set of three numbers that shows the relationship among the quantities.
- Create your sets of three numbers in three different ways:
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
INTERACTIVE: Price per Gallon
Dollars and Pesos
Lesson Guide
Have the students look up the current exchange rate of pesos per dollar or dollars per peso. Students fill in a table reflecting one of those rates.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students can enter any numbers into the tables as long as the relationship between the numbers is correct. As students work, identify a variety of work with an eye to making connections among different methods. For example, look for the following different approaches:
- Choosing a number of dollars and a rate, and then calculating a number of pesos
- Choosing a number of pesos and a rate, and then calculating a number of dollars.
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
- Answers will vary, but the relationships should show that dollars per peso is equal to dollars divided by pesos.
Work Time
Dollars and Pesos
In this problem, you will work with three quantities: dollars, pesos, and dollars per peso.
Create a set of three numbers that show the relationship among the quantities.
- Create your sets of three numbers in three different ways:
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
INTERACTIVE: Dollars and Pesos
Hours, Speed, and Miles
Lesson Guide
Student will fill in a table showing the relationship of hours, speed, and miles.
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
- Answers will vary, but the relationships should show that speed is equal to the miles divided by the hours.
Work Time
Hours, Speed, and Miles
In this problem, you will work with three quantities: hours, speed, and miles.
Create a set of three numbers that show the relationship among the quantities.
- Create your sets of three numbers in three different ways:
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
Stack of Books
Lesson guide
Students will fill in a table showing the relationship of the number of books in a stack, the height of the stack, and the thickness of each book (inches per book).
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Do your answers make sense?
- Explain the relationship among your numbers in this problem.
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
- Answers will vary, but the relationships should show that the thickness of a book is equal to the height of the stack divided by the number of books.
Work Time
Stack of Books
In this problem, you will work with three quantities: the number of books in a stack, the height of the stack, and the thickness of each book (inches per book).
Create a set of three numbers that show the relationship among the quantities.
- Create your sets of three numbers in three different ways:
- The first set contains any numbers.
- The second set contains numbers greater than 10.
- The third set contains decimal numbers.
INTERACTIVE: Stack of Books
Prepare a Presentation
Lesson Guide
Students fill in a table on a runner to find out if a runner runs at a constant speed. Then they prepare a presentation on their method.
Preparing for Ways of Thinking
Look for students who understand that they can choose any two numbers to find the third number. These students are using a general method to solve all rate problems.
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- Can you use your definition of rate to help you get started?
Student has an incorrect solution.
- Have you checked your work?
- Did you remember to convert minutes to hours?
- Do your answers make sense?
- Where do you see the rate in this problem? Describe it.
Student has a solution.
- Why did you approach this problem in the way that you did?
- Could you have used another method to solve this problem? Explain.
- What still confuses you about rate?
Answers
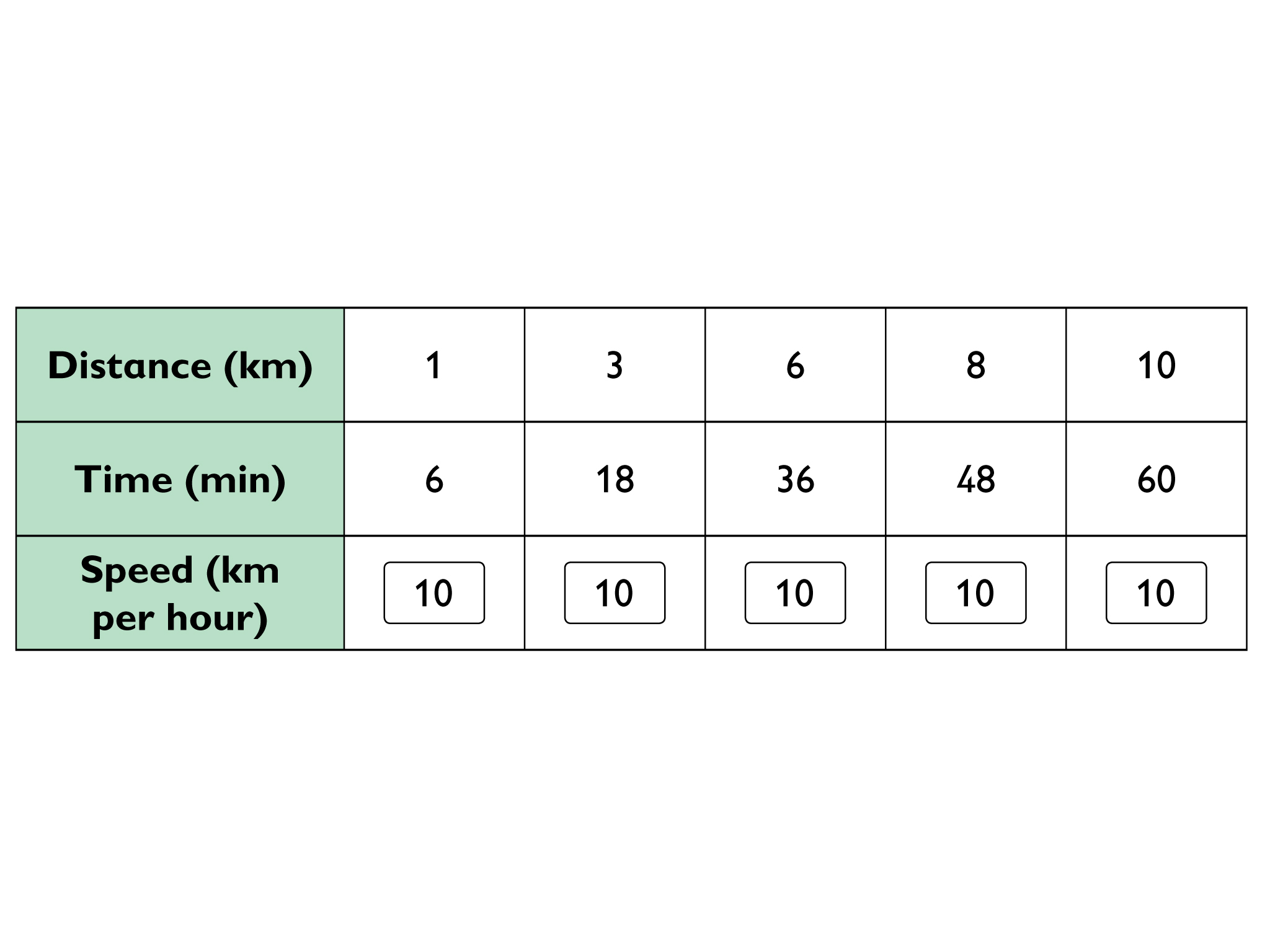
Yes. The table supports the statement that the runner runs at a constant speed.
10 kilometers per hour
Work Time
Prepare a Presentation
Prepare a presentation of your work.
- The runner runs at a constant speed.
- Does the table support this statement?
- Complete the table.
- Express the speed of the runner in kilometers per hour.
INTERACTIVE: Prepare a Presentation
Make Connections
Lesson Guide
By the end of the discussion, students should understand each other's methods and make connections between methods. All students should also understand that given any two values in a rate situation, they can find the third value. Encourage students to critique each method.
Mathematics
Discuss the different approaches students use. Ask questions such as the following to help students critique each other's work and to help them see relationships among the different methods:
- How did the student make sense of the problem?
- What was similar about their approaches?
- What was different?
- Did anyone try a method that did not work? What did you do? Why didn't your method work?
Performance Task
Ways of Thinking: Make Connections
As you listen to other students present their work, find ways to understand how to think about rate.
Hint:
As your classmates present, ask questions such as:
- Where is the rate in your numbers?
- Where do you see the other two quantities?
- How would you describe the relationship among the three numbers?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review students' reflections.
If any reflections look interesting enough to pursue later, share them with the class at an appropriate time.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I still wonder about rates is …