- Author:
- Chris Adcock
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Container
Flow Rate
Water Efficiency
Gallery Problems Exercise

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery Descriptions
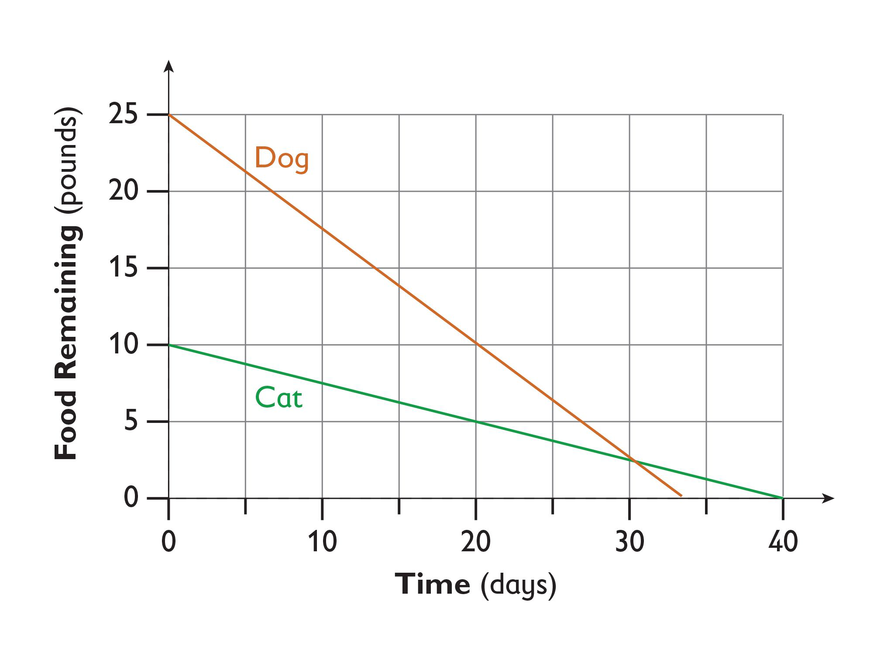
Dog and Cat
Students refer to a pre-made graph showing how much dry food a dog eats and how much dry food a cat eats over the same time period. They analyze the graph and list specific information they can conclude from the graph.
Faucet Rate Problem
Students perform research on the Internet about standard water flow rates of bathroom faucets in the United States. They test faucets at home or at school and prepare responses to the questions.
Shower versus Bath
Students will use their knowledge of rates to figure out which uses less water, a shower or a bath.
Laps, Miles, Kilometers
Students use rates to convert measures given in laps, kilometers, and miles. They justify their reasons for ordering distances given in these three units.
Paper Problem
Students write and use formulas for heights of stacks of paper. They practice writing rates for h in terms of n and for n in terms of h.
Three Scales
Students use a triple number line to convert among the units laps on a track, kilometers, and miles. Given one number line, they mark two other number lines to show equal distances in the units.
Water Problem
This problem begins with a video of a cube container being filled with colored water. Students determine what information they'd need in order to figure out the volume of water in the cube at any time.
Dog and Cat
Answers
Students should recognize that the dog ate 25 pounds in about 33 days and the cat ate 10 pounds in 40 days.
More complex relationships students might notice:
- The slopes are constant, meaning that each pet ate the same amount of food day after day. In other words, the cat did not eat a greater quantity of food on one day than on any other day.
- The steepness of the slopes tells students that the dog ate more food per day than the cat. Students can recognize this at any part of the graph regardless of how much food either pet has eaten.
- Students can also deduce the rate of food eaten per day. The dog ate about pound of food per day, and the cat ate pound of food per day.
Spend time with students to bring out all the information they can get from the graph.
Work Time
Dog and Cat
Rosa’s dog eats dry dog food. Rosa’s cat eats dry cat food. Each animal started eating from a new bag of food on the same day. Rosa graphed the situation as shown.
- What information can you conclude from the graph? Be specific.
Faucet Rate Problem
Answers
- Answers will vary.
Work Time
Faucet Rate Problem
Research on the Internet the standards for water flow rates for bathroom faucets in the United States. You should find that the maximum rate should be about 0.5 gallon per minute.
- Test some of the faucets in your school or home.
- Turn the fixture to its fully open position.
- Place a container under the fixture and collect the flowing water for 10 seconds.
- Measure the quantity of water in the container.
- Convert the measurement to gallons. Use the conversion factor 1 gallon = 16 cups.
- Multiply the measured quantity of water by 6 to calculate the flow rate in gallons per minute (for example, 0.25 gallon × 6 = 1.5 gallons per minute).
- Do the faucets you tested have standard flow rates?
Shower versus Bath
Answers
- The answer is a student prediction; answers can vary.
- You need to know the durations of the shower and the bath (the time it takes to fill it) and the water rate in gallons per second.
- The rate of the tub flow is . The rate of the shower flow is .
- Using reasoning, the shower takes about three times as long to fill the gallon as the bath. The shower is 28% longer than the bath. If the bath takes x gallons, then the shower takes , or about gallons. So the shower uses about of the gallons used in the bath. Or, students can use the rate of gallons per second to find the amount of water used. Answers will vary depending on place value rounding.
Bath: 6 minutes 15 seconds is equal to 375 seconds.
Shower: - The answer would change if:
- The shower were longer (about minutes or more)
- The rate of water out of the shower head was faster and it filled the gallon as fast as the tub faucet
- Using that same amount of water, you can take approximately a 19-minute shower. Filling for 6 minutes and 15 seconds at 1 gallon per 11 seconds, the tub holds approximately 34 gallons. While showering at 33 seconds per gallon, it would take about 19 minutes to use 34 gallons.
Work Time
Shower versus Bath
Watch the video Water Efficiency.
- Which do you think uses less water, a shower or a bath? Why?
- What information do you need to figure out which one uses more water?
- Watch the video Flow Rate and use the information in the video to calculate the flow rate of a shower faucet and a bath faucet.
- Watch the video Bath versus Shower. Use the information in the video to determine which uses more water, a bath or an average shower.
- How would the situation need to change to reverse the answer to problem 4?
- Given the information you have, how long a shower can be taken to use the same amount of water as the bath used?
VIDEO: Water Efficiency
VIDEO: Flow Rate
VIDEO: Bath versus Shower
Laps, Miles, Kilometers
Answers
- If 1 lap = 0.4 km, then 2.5 lap = 1 km.
- If 1 lap = 0.25 mi, then 4 laps =1 mi
Converting each girl's distance to laps will make it easier to compare the distances.
Rosa ran 14 laps.
Emma ran 5 km.
Mina ran 3 miles.
- Rosa ran the longest distance: 14 laps.
- Mina ran the shortest distance: 12 laps.
Work Time
Laps, Miles, and Kilometers
A runner can measure her progress in terms of laps, miles, or kilometers.
A sign is posted at a track that gives the distances in miles and in kilometers for one-half of a lap.
lap = miles, or 0.2 km
Rosa ran 14 laps.
Emma ran 5 km.
Mina ran 3 mi.
- Who ran the longest distance? Justify your answer mathematically.
- Who ran the shortest distance? Justify your answer mathematically.
Paper Problem
Answers
- 6 ⋅ 1.25 = 7.5; A stack of 600 sheets would be 7.5 centimeters high.
- 2.5 ⋅ 1.25 = 3.125; A stack of 250 sheets would be 3.125 centimeters high.
- ; One sheet of paper would be 0.0125 centimeter high.
h = 0.0125n
- ; It takes 720 sheets to make a stack that is 9 centimeters high.
- ; It takes 540 sheets to make a stack that is 6.75 centimeters high.
- ; It takes 80 sheets to make a stack that is 1 centimeter high.
In , the constant represents the height of each sheet of paper in centimeters. In , the constant represents the number of sheets in a centimeter.
Work Time
Paper Problem
The stack of paper pictured is 100 sheets.
- Find the height in centimeters of the following:
- 600-sheet stack
- 250-sheet stack
- 1 sheet of paper
- Let equal the number of sheets of paper, and let equal the height of the stack in cm. Write a formula for in terms of .
- Find the number of sheets of paper it takes to make a stack with the given heights:
- 9 centimeters
- 6.75 centimeters
- 1 centimeter
- Write a formula for in terms of .
- What does the constant represent in each of your two formulas?
A 100-sheet stack of a different kind of paper is 1.6 centimeters high. Let equal the number of sheets of paper, and let equal the height.
- Write a formula for in terms of .
- Write a formula for in terms of .
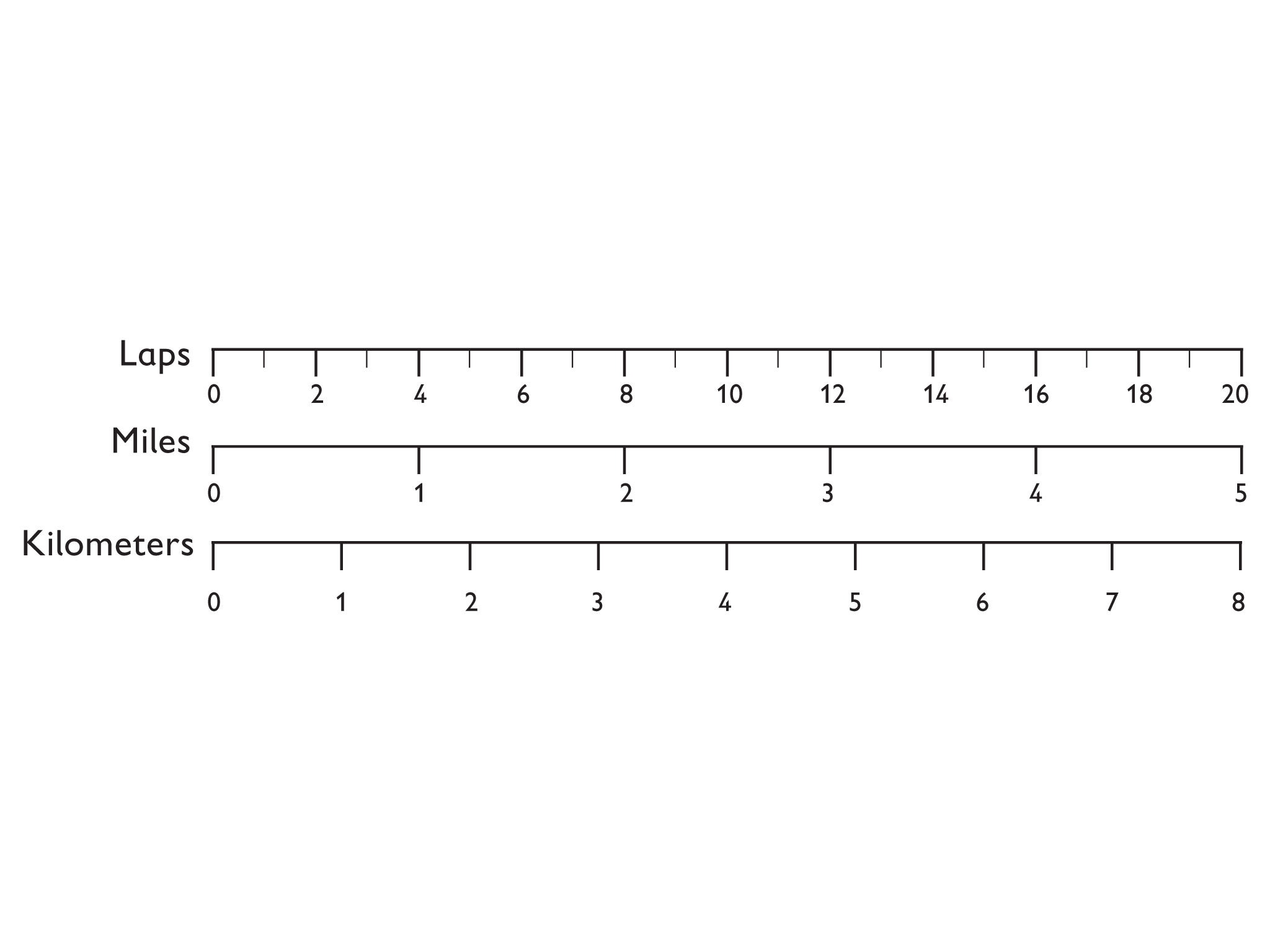
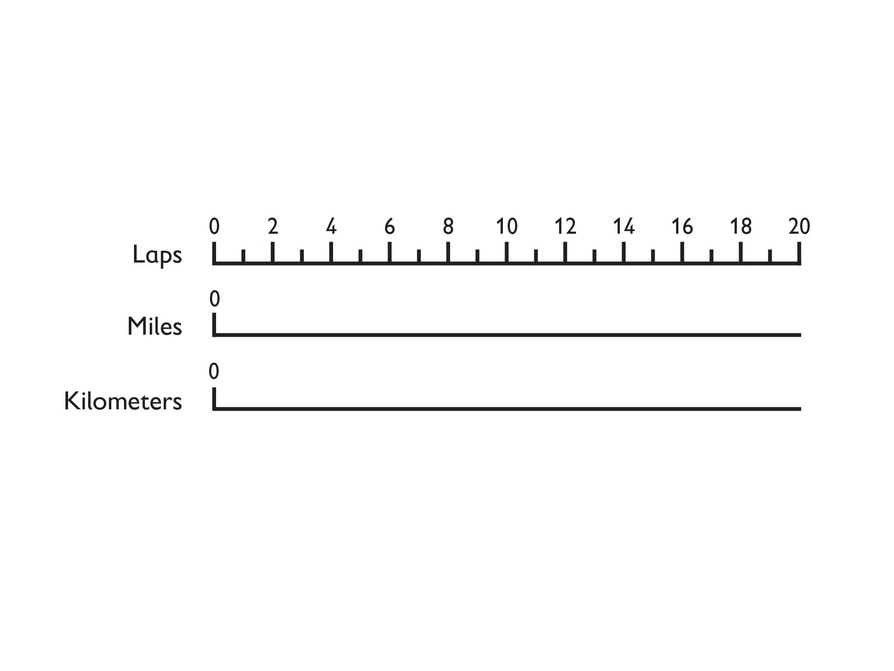
Three Scales
Answers
- A mile is longer than a kilometer. There are fewer miles than kilometers in laps.
- Approximately to kilometer is equal to 1 lap.
- Approximately mile is equal to 1 lap.
- Approximately kilometer is equal to 1 mile.
Work Time
Three Scales
Emma reads this information in a healthclub’s brochure:
“On our track, 1 mi equals 4 laps. On the same track, 1 km equals 2.5 laps.”
- Look at the image and use it to help you with the following:
- Draw three number lines arranged as shown. Work carefully, and use a ruler.
- Mark the Miles scale and the Kilometers scale so that the two scales show the same distance as the Laps scale.
- Use your triple number line to answer these questions:
- Which is longer, a mile or a kilometer?
- Approximately how many kilometers equal 1 lap?
- Approximately how many miles equal 1 lap?
- Approximately how many kilometers equal 1 mile?
Water Problem
Answers
- You would need to know the dimensions of the container and the height of the water at that point in time.
- Volume = width • length • height
If h is the height of the water in inches and v is the volume in cubic inches, then v = 3 ⋅ 3 ⋅ h = 9h. The height h can range from 0 to 3 inches. The volume can range from 0 to 27 cubic inches.
Work Time
Water Problem
Watch the Container video, which shows water filling up a cube container.
- What do you need to know about the situation to determine the volume of the water in the cube container at any point in time?
- If the width and the length of the cube container are each 3 inches, describe the situation using your knowledge of rates and representations of rates.
VIDEO: Container