- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Defining Rate Discussion

Overview
In this lesson, students define rate. After coming up with a preliminary definition on their own, students identify situations that describe rates and situations that do not.
Students determine what is common among rate situations and then revise their definitions of rate based on these observations. Students present and discuss their work and together create a class definition. They compare the class definition of rate with the Glossary definition and revise the class definition as needed.
Key Concepts
A good definition of rate has to be precise, yet general enough to be useful in a variety of situations. For example, the statement “a rate compares two quantities” is true, but it is so general that it is not helpful. The statement “speed is a rate” is true, but it is not useful in determining whether unit price or population density are rates.
A good definition of rate needs to state that a rate is a single quantity, expressed with a unit of the form A per B, and derived from a comparison by division of two measures of a single situation.
Goals and Learning Objectives
- Gain a deeper understanding of rate by developing, refining, testing, and then refining again a definition of rate.
- Use a definition of rate to determine the kinds of situations that are rate situations and to recognize rates in new and different situations.
- Understand the importance of precision in communicating mathematical concepts.
Using Mathematical Definitions
Lesson Guide
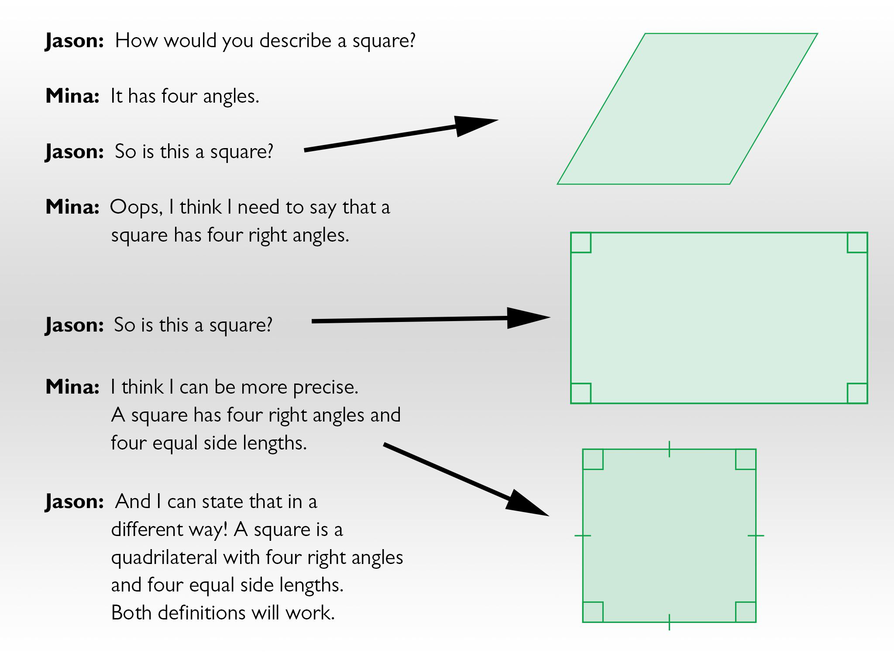
Have students read the conversation to help them understand what precision means. Ask students to talk with their partners about how the description of the square became more and more precise.
Tell students that today they will create a definition of rate and evaluate the precision of their definitions.
Mathematical Practices in Action
Mathematical Practice 6: Attend to precision.
Tell students that mathematicians are concerned with precision because it requires precision to effectively communicate mathematical ideas to others.
Point out that students have already been using this math practice since their first math lesson; they will continue to use it for the rest of the school year and throughout their lives.
Ask students to think back about the work they have done so far with rate and then consider how they might define the word rate.
Give them a few sample definitions that lack precision:
- “Speed is a rate.” Acknowledge that speed is a rate, but challenge students to see that this definition is not very useful or complete.
- “A rate compares two quantities.” Although this definition is accurate, it is so general that it is not helpful. Point out, however, that a good definition of rate has to be general enough to be useful in a variety of situations.
Opening
Using Mathematical Definitions
Attending to precision is an important mathematical practice. One of the most important parts of attending to precision is developing and using clear definitions. In this lesson, you will write a definition of rate and then apply the definition to see if it is precise enough to be useful.
Think about and use this mathematical practice of attending to precision in this class, in other math classes that you take, and as you use mathematics in your life.
- Read the conversation.
- How is the conversation an example of attending to precision?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will write a precise and useable definition of rate.
To define rate in this lesson, students will complete several steps. They will begin by coming up with a preliminary definition of rate. Next they will revise their definitions after comparing situations that do and do not describe rates. Finally, students will create a class definition of rate and then compare this definition to a formal definition.
Opening
Write a precise and usable definition of rate.
Define Rate
Lesson Guide
Begin by having students write a preliminary definition of rate.
Interventions
Student is having difficulty getting started.
- Describe the task in your own words.
- What are some examples of rate that you have done in this unit?
- Using one of those examples, how would you define rate?
Student has a very limited definition.
- Would that work if you think about rate as (fill in a situation such as population density or price).
Answer
- Answers will vary.
Work Time
Define Rate
Think about the different rates you have worked with in previous lessons. Use what you know about rates to write a definition of the term rate.
Hint:
- What does a rate compare?
- What word is usually used to express a rate?
- Does a rate involve subtraction, multiplication, or division?
Identify Rates
Lesson Guide
In this activity, students review different situation cards. They sort the cards into three categories: rate, not a rate, not sure. After students have gone through all the card, they should look for similarities in the situations they defined as rate situations. Students should revise their definitions based on their observations.
Interventions
Student has difficulty getting started.
- Describe the Task in your own words to your partner.
- How can you decide if a situation describes a rate?
- Can you use your definition of rate to help you?
Student has an incorrect solution.
- How did you decide whether a situation described a rate?
- Explain why you think this situation describes a rate.
- Explain why you think this situation does not describe a rate.
- Would it help if you revised your definition of rate?
- Can you go back and reexamine the cards in the “not sure" category?
Student has a solution.
- Explain your approach for determining whether or not situations are rates.
- Was your definition of rate helpful? Why or why not?
- What makes a situation a rate situation?
- What makes a situation not a rate situation?
- Can you make your definition of rate more precise?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Identify students who put cards in the “not sure” category, but then later correctly moved the card into one of the other two categories. These students are persevering to find a solution.
Mathematical Practice 2: Reason abstractly and quantitatively.
- Students will use reasoning to determine whether or not a situation represents a rate.
Mathematical Practice 7: Look for and make use of structure.
- Students will look at the structure of the situation to determine whether or not it is a rate.
Possible Answers
- Solutions will vary because several situations could be interpreted in different ways:
- Some students might say that a stack of books is not a rate. Other students might point out that all the books are equal in height, and thus the books describe the rate in inches per book.
- The pieces of ribbon could simply be three pieces of ribbon, in which case the situation does not describe a rate. However, if students explain the situation by saying that a specific length of ribbon is needed to make a bow, then it does describe a rate (length per segment)
The relationship between students and computers could be described by a ratio; but if the relationship is expressed as a single quantity of two students per one computer, it is a rate.
Explanations will vary.
- Definitions will vary, so the fit of the situations to the definition will vary as well.
Work Time
Identify Rates
Look at the situations cards and sort them into the following categories:
- Situations that describe rates
- Situations that do not describe rates
- Situations in which you are not sure whether or not it describes rates
HANDOUT: Card Sort
Hint:
- Sort the cards into the appropriate categories.
- For each situation, explain your thinking to your partner.
- If a situation describes a rate, check it against your definition.
- If the situation does not describe a rate or if it is not possible to tell, explain why not.
- Use your definition of rate to help you decide whether or not each situation describes a rate. If your definition is not helpful, revise your definition.
Define Rate
Lesson Guide
Sample definition: A rate is a single quantity that compares two quantities with different units. It is expressed with a unit of the form A per B, and is derived from a comparison by the division of two quantities in a single situation.
Interventions
Student is having difficulty getting started.
- Name one situation that describes a rate.
- Check the example against your definition. Does your definition work for that example?
Student has a very limited definition.
- Would that work if you think about rate as [fill in a situation]?
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Students will revise their definitions of rate to be more precise.
Work Time
Define Rate
Think about the situations that you categorized as describing a rate. What do these situations have in common?
By identifying things that these situations have in common, you can make your definition of rate more precise.
- Review your initial definition of rate. Then, using what you have learned from the previous task, refine your definition to make it more precise.
Prepare a Presentation
Lesson Guide
Student will revise their definitions of rate to make the definitions more precise.
Have students prepare presentations of their work. Students' presentations should include their revised definitions of rate and a discussion of how specific situations either fit the definition or did not fit the definition.
Preparing for Ways of Thinking
Look for students who are able to make sense of the quantities in the situations and express the quantities as rates. Also look for students who accurately explain why particular situations do not describe rates.
Watch for students who see the similarities in the rate situations and use these similarities to refine their definitions of rate.
Challenge Problem
Answers
- Answers will vary.
Work Time
Prepare a Presentation
Prepare a presentation about your work.
- Write your revised definition of rate.
- Select one situation that you are sure describes a rate, and explain why it fits your definition.
- Select one situation that you are sure does not describe a rate, and explain why your definition excludes it.
- Select one situation that you are not sure about to discuss with the class.
Challenge Problem
Read the definition of rate in the Glossary. Then go back and review your solutions with this definition in mind.
- Would you categorize the situations in the same way?
- Can you think of any situation that does describe a rate using your definition but does not describe a rate using the Glossary definition?
- Can you think of any situation that does describe a rate using the Glossary definition but does not describe a rate using your definition?
Make Connections
Lesson Guide
The goal of this discussion is for students to test the limitations of their own definitions of rate in order to generate a more precise class definition. Students will then compare the class definition with the Glossary definition to further test and refine the class definition.
At the end of the presentations, display the situations that all students agreed were rates. Ask students what these situations have in common. Use this discussion and students' definitions that they shared during their presentations to write a class definition of rate.
Next, show some situations that not all students agreed on. Focus the discussion on explaining why the situation does or does not describe a rate. Use this discussion to help students evaluate the class definition of rate and refine it as needed.
To facilitate the discussion and highlight mathematical practices, ask questions such as the following:
- [Name] says that this situation is a rate situation. Do you agree? Explain why or why not.
- [Name] says that this situation is not a rate situation. Do you agree? Explain why or why not.
- I noticed that you initially categorized this situation in the “I can't tell” category, but then later you moved categorized it in another category. What helped you to persevere in finding better ways to describe the situation?
- How did finding the similarities among the situations in the “describes a rate” and the “does not describe a rate” categories help you revise your definition of rate?
- How can we revise our class definition of rate to make it more precise?
ELL: When engaging in oral discussions that require understanding of academic vocabulary recently introduced, monitor that ELLs are familiar with the vocabulary and are able to apply it. Monitor that all students are on topic and ask probing questions when in doubt.
SWD: While students have had multiple exposures to the domain-specific terms, students with disabilities will benefit from repetition and review of these terms. As students move through the lesson, check to ensure they understand the meaning of included domain-specific vocabulary. Use every opportunity to review and reinforce the meaning of domain-specific terms to promote comprehension and recall.
Performance Task
Ways of Thinking: Make Connections
Share your presentation.
- Be ready to defend your solutions by using your definition of rate.
- As other students present, challenge answers that differ from your own by presenting your ideas.
Hint:
As your classmates present, ask questions such as:
- Why did you put this card in the “describes a rate” category? What makes the situation a rate situation?
- Why did you put this card in the “does not describe a rate” category? What makes this situation not a rate situation?
A Final Definition of Rate
Lesson guide
Students will write a final definition for rate.
A Possible Definition
A rate is a single quantity that compares two quantities with different units. It is expressed with a unit of the form A per B, and is derived from a comparison by the division of two quantities in a single situation.
SWD: Ask students to build a concept map about rate. Concept maps are an excellent way to access students' prior knowledge.
Formative Assessment
Summary of the Math: A Final Definition of Rate
- Write a final definition of rate.
Hint:
Check your summary
- Does your definition provide enough specific information to be useful, but enough general information so that it can be applied to a variety of situations?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review students' reflections.
If you find some reflections interesting enough to pursue later, share them with the class at an appropriate time.
Work Time
Reflection
Reflecting on your work is another way to solidify your understanding of a mathematical concept.
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
What I learned about defining rate is …