- Author:
- Chris Adcock
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Interactive Ruler
Reviewing Conversion Factors

Overview
In this lesson, students use a ruler that measures both inches and centimeters to find conversion factors for converting inches to centimeters and centimeters to inches.
Key Concepts
Rates can be used to convert a measurement in one unit to a corresponding measurement in another unit. We call rates that are used for such purposes conversion factors.
The conversion factor 2.54 centimeters per inch is used to convert a measurement in inches to a measurement in centimeters (or, from the English system to the metric system).
The conversion factor 0.3937 inches per centimeter is used to convert a measurement in centimeters to a measurement in inches (or, from the metric system to the English system).
In the calculation, the inch units cancel out and the remaining centimeter units are the units of the answer, or vice versa.
Goals and Learning Objectives
- Explore rate in the context of finding and using conversion factors.
- Understand that there are two conversion factors that translate a measurement in one unit to a corresponding measurement in another unit, and that these two conversion factors are inverses of one another.
Explore Centimeters and Inches
Lesson Guide
Students will continue their investigation of rates by thinking about how to convert between inches and centimeters.
Give students a few minutes to investigate the two sliders on the interactive ruler. Then hold a class discussion in which students discuss their observations. By the end of the discussion, make sure that students understand that they were using the two sliders to find rates—specifically, rates called conversion factors.
ELL: To help students access the mathematics in this problem, review key information before beginning the problem. It would be helpful to walk students through the problem.
Mathematics
During the class discussion, ask students what they notice about the ruler and the sliders. Students may make the following observations:
- Using the top slider, it is easy to locate parts of an inch.
- Using the bottom slider, it is easy to locate parts of a centimeter.
- The inch scale and the centimeter scale are arranged much like a double number line.
- By moving the top slider to any number on the inch scale, the ruler gives a measurement in centimeters.
- By moving the bottom slider to any number on the centimeter scale, the ruler gives a measurement in inches.
This alignment allows students to directly observe the relationship between inches and centimeters. If students do not come to the understanding themselves, point out that the relationship between inches and centimeters is a rate.
Explain that the term conversion factor is used to describe the rate when dealing with conversions between measurements—just as speed and population density were used to describe the rate in other situations.
Explain that by moving the top slider to 1 inch, students can find the conversion factor for converting inches to centimeters. By moving the bottom slider to 1 centimeter, students can find the conversion factor for converting centimeters to inches.
Opening
Explore Centimeters and Inches
Open the interactive and move the slider above the ruler to 1 inch.
About how many centimeters are equal to 1 inch?Move the slider below the ruler to 1 centimeter.
About how many inches are equal to 1 centimeter?
INTERACTIVE: Interactive Ruler
Hint:
Use the sliders on the ruler to find rates.
Math Mission
Lesson Guide
Discuss the Math Mission. Explain how to use the information on the ruler to define two conversion factors and how to use those conversion factors to solve problems. Students will use the ruler to find conversion factors for converting inches to centimeters and centimeters to inches.
Opening
Find conversion factors and use them to solve problems.
Unit Conversions
Lesson Guide
Identify students who find and use the conversion factors correctly, as well as students who use the wrong conversion factors to solve the problems.
ELL: Consider allowing, or even encouraging, students to sketch a diagram to go along with the problems they create to share with the class. This will help ELLs better understand the problems presented by their classmates. Diagrams also allow ELLs another way to communicate concepts that may be difficult for them to express in English.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Find several students who use different strategies to make sense of the problems.
Mathematical Practice 5: Use appropriate tools strategically.
- Look for students who use the ruler to first find conversion factors and then calculate the lengths, and for students who extend their thinking with the ruler by using other tools such as a double number line or a table.
Mathematical Practice 6: Attend to precision.
- Identify students who are careful about specifying the proper units of measure in their work.
Interventions
Student has difficulty getting started.
- What is a rate?
- How can you find the number of centimeters per inch?
- How can you find the number of inches per centimeter?
Student does not understand how to use the ruler.
- What does the top scale show?
- What does the bottom scale show?
- If you move the top slider to 1 inch, what is the corresponding measurement in centimeters?
- If you move the bottom slider to 1 centimeter, what is the corresponding measurement in inches?
Student has a solution.
- Explain how you converted 9 inches into centimeters.
- Explain how you converted 25 centimeters into inches.
- Where do you see a rate in each of your solutions?
- How did the ruler help you solve the problem?
Answers
- The conversion factor for converting inches to centimeters is 2.54 centimeters per inch.
- 9 inches = 22.86 centimeters
- The conversion factor for converting centimeters to inches is 0.3937 inches per centimeter.
- 25 centimeters = 9.8425 inches
Work Time
Unit Conversions
A conversion factor is a rate used to convert from one unit of measure to another unit of measure, where the types of things being measured are the same (for example, length to length or weight to weight). Only the units are different.
- Find a conversion factor that you can use to convert inches into centimeters.
- Use your rate to convert 9 inches into centimeters. Check your answer using the ruler.
- Find a conversion factor that you can use to convert centimeters into inches.
- Use your rate to convert 25 centimeters into inches. Check your answer using the ruler.
INTERACTIVE: Ruler
Hint:
- Use the ruler to find the conversion factor of inches per centimeter or centimeters per inch.
- Would the number of inches be more or less than the number of centimeters for the same length?
- Once you have the rate, what operation do you need to use to make the conversion?
- Can you use a double number line or a ratio table to help you make conversions?
Prepare a Presentation
Lesson Guide
Students will prepare presentations about their methods of converting from inches to centimeters.
 Preparing for Ways of Thinking
Preparing for Ways of Thinking
Look for students who do the following:
- Represent the ruler in the form of a double number line or a table.
- Use conversion factors to calculate the length in centimeters of 9 inches and to calculate the length in inches of 25 centimeters.
Challenge Problem
Answer
- Answers will vary.
Work Time
Prepare a Presentation
- Prepare a presentation about the method you used to find the conversion factors to convert from one unit to another.
Challenge Problem
- Write an explanation of the similarities and differences among unit price, fuel efficiency, population density, speed, and conversion factors. Be prepared to present your explanation to the class.
Make Connections
Lesson Guide
During the discussion, students should understand each other's methods and make connections among methods.
Select a variety of work with an eye to making connections between different representations. Display all of these solution methods:
- Representing the ruler in the form of a double number line or a table
- Using conversion factors to calculate the length in centimeters of 9 inches and to calculate the length in inches of 25 centimeters
If anyone has a good explanation from the Challenge Problem, have them share it.
SWD: Struggling students have difficulty articulating their thinking, constructing viable arguments, and critiquing each other's work. Consider pulling a small group of struggling students to provide guided modeling and more support. If pulling a small group is not feasible, strategically selecting partners that can articulate their thinking and are able to peer mentor will be beneficial to struggling students.
ELL: Encourage students to use the academic vocabulary they learned. Encourage all students to listen attentively to each other, and make sure all students know about the importance of being patient when non-native speakers express themselves—possibly at a slower pace or with sentences that are a little harder to follow.
Mathematics
Ask students who used different methods (for example, a table, a double number line, or calculations with a conversion factor) to present. As part of the discussion, challenge students to compare these representations of the problem by asking the following questions:
- How did the student make sense of the problem and how did they model the problem situation mathematically? What is similar about their approaches? What is different?
- Which method helps you see the structure of the mathematics most clearly? Which method makes the most sense to you?
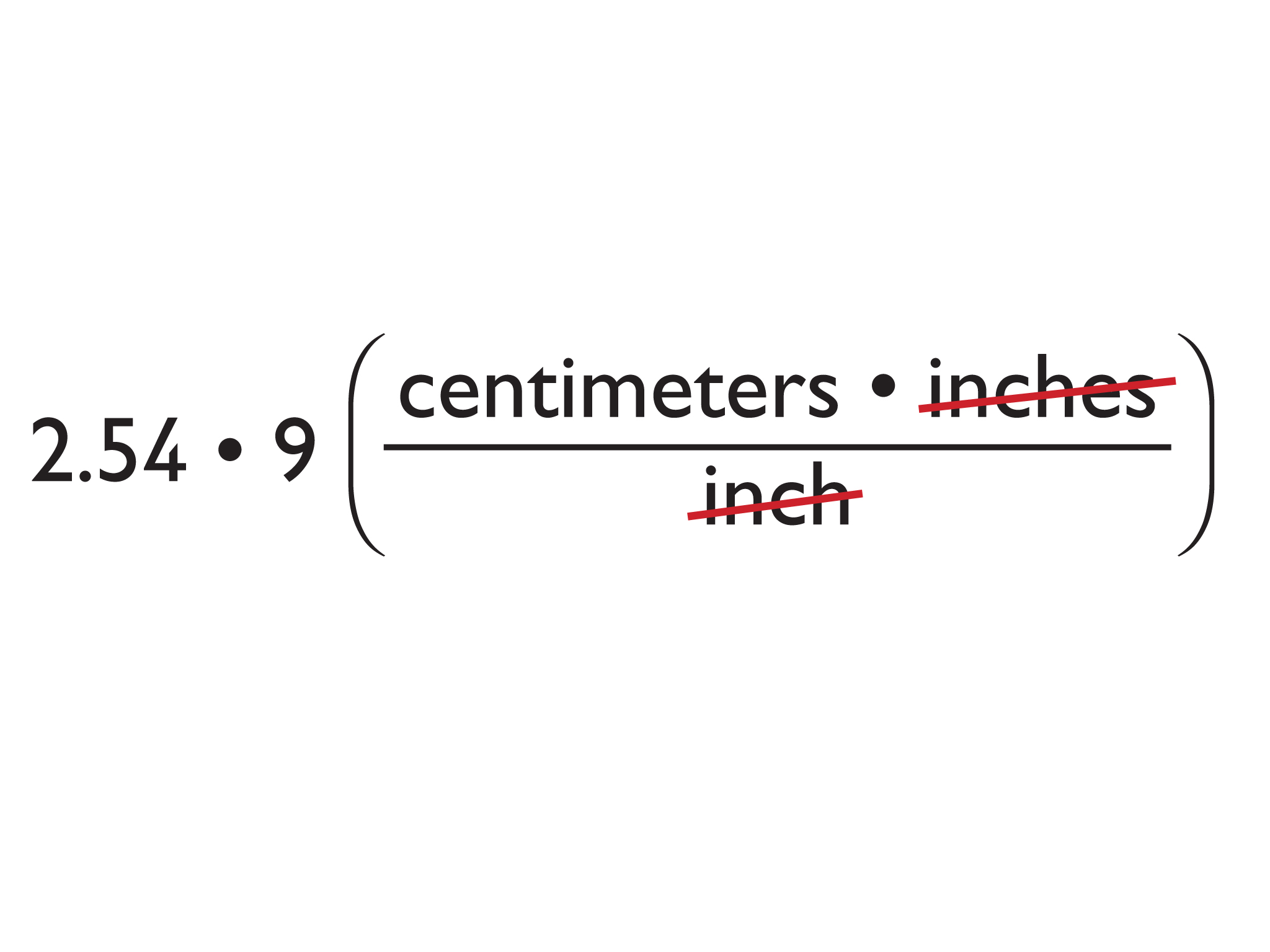
Part of a solid understanding of multiplying by a conversion factor—or by any rate—is making sense of the units. Focus on a piece of student work that has the correct calculation for the number of centimeters in 9 inches:
Help students reason that the conversion factor 2.54 centimeters/inch means that each inch is 2.54 centimeters long. A length of 9 inches has 9 one-inch segments. Each of those segments is 2.54 centimeters long. The whole 9-inch length is 2.54 ⋅ 9 = 22.86 centimeters long. Once students can explain why the units of the answer must be centimeters, display the work and show the class that the problem can be written like this:
The inch units in the numerator and in the denominator cancel out and the unit that remains is centimeters.
Be sure to introduce the canceling process before engaging the students in a discussion to make sense of the concept so students don't see the canceling as “magic.”
Performance Task
Ways of Thinking: Make Connections
Did any of your classmates use a method that is different from the one you used to find the conversion factors and solve the problems?
- Take notes on the different approaches.
Hint:
As your classmates present, ask questions such as:
- Explain how you used the ruler to find conversion factors.
- Where do you see the conversion factor in your method? Where do you see the answer?
- Why is multiplication rather than division the correct operation to use to make the conversions?
- What happened to the units as you performed the multiplication?
Miles and Kilometers
Interventions
Student has difficulty getting started.
- What is the given rate?
- Can you use the given rate to find the number of kilometers in 1 mile? What would you do to find the number of kilometers in 10 miles?
- What unit needs to be converted when going from miles per hour to kilometers per hour—miles, kilometers, or hours?
Answers
- There are approximately 16 kilometers in 10 miles.
- The speed limit is 88 kilometers per hour.
- The distance between New York City and Los Angeles is 3,912 kilometers.
Work Time
Miles and Kilometers
There are approximately 1.6 kilometers per mile. Use this conversion factor to solve these problems.
- How many kilometers are in 10 miles?
- How can you express the speed limit 55 miles per hour in kilometers per hour?
- The distance between New York City, New York, and Los Angeles, California, is 2,445 miles. What is this distance in kilometers?
Hint:
- Would the number of kilometers be more or less than the number of miles?
- If you have the conversion factor, what operation do you need to use to make the conversion?
Conversion Factors as Rates
A Possible Summary
Conversion factors are rates that convert measurements in one unit to corresponding measurements in another unit. Two conversion factors are 2.54 centimeters per inch (for converting inches to centimeters) and 0.3937 inches per centimeter (for converting centimeters to inches).
Additional Discussion Points
- Conversion factors are rates that are used to convert a measurement in one unit to a corresponding measurement in another unit.
- The conversion factor of approximately 1.6 kilometers per mile is used to convert a measurement in miles to a measurement in kilometers.
- In the multiplication centimeterinch⋅inch, the inch units cancel out and the remaining centimeter unit is the unit of the answer.
Formative Assessment
Summary of the Math: Conversion Factors as Rates
Write a summary of what you have learned about conversion factors.
Hint:
Check your summary.
- Does your summary explain what a conversion factor is and how to use it?
- Does your summary include the term rate ?
- Does your summary describe how to convert inches to centimeters and centimeters to inches?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review students' reflections. If any reflections look interesting enough to pursue later make a note of them and consider sharing them with the class when appropriate.
It may be helpful to provide students with scaffolding questions or a bulleted list of ideas that were discussed for students to write about. In addition to the sentence starter, students may also benefit from paragraph frames such as “So far, I have completed … . I have noticed that … . The parts I found challenging were … .”
SWD: Some students may struggle to initiate writing for this reflection. Prompt them to refer to the sentence starter as a support.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
What I learned about conversion factors from someone else in class is …