- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
House Plans
House Plans

Overview
Students are introduced to real-world applications of geometry and measurement by looking at architectural plans. Students also begin to get familiar with reading architectural plans and thinking about scale.
Key Concepts
Since this lesson is exploratory, all of the mathematics discussed will be informal. However, most of the mathematics that students will see in the unit is introduced in this lesson. Students look at length, area, surface area, and volume and examine how these measurements pertain to architectural plans and determining building costs. Students will also consider scale and how scale is used in architectural plans and math drawings.
Goals
- Think about what measurements are needed to build a building.
- Think about what measurements determine the cost of a building.
- Think about how scale is used in math drawings.
SWD: Check in to ensure that students understand the meaning of domain-specific vocabulary terms such as dimensions, scale, and area. You may also need to clarify the meaning of the word contract for some students.
ELL: Consider having students compile a list or resource with key vocabulary terms for this unit.
House Plans
Lesson Guide
Have the House Plans video ready to show at the start of the lesson.
ELL: When showing the video, be sure that ELLs can follow the explanations. Pause the video, as necessary, to allow ELLs time to process the information. Ask students if they need to watch it a second time. Consider asking some questions to make sure students understand the video.
SWD: It may be helpful to allow students with language processing or attention variability behaviors to preview the video. Another way to support students’ understanding of the video is to cue students to “look out for” particular elements of the video. You may even provide a list of key ideas for students to review prior to viewing.
Mathematics
Briefly discuss the opening questions. Take only a few observations, as students will be answering these questions in more depth during the work period.
Make sure that students understand how to read the house plans. The floor plan matches up with the front elevation of the house (compare window and door locations on the plan with the 3-D house model). The side elevation of the house also matches the floor plan, but in the video the side view is not located directly beside the plan.
Opening
House Plans
Watch the House Plans video.
- Do you think you could determine any of the actual measurements of the house based on these house plans?
- Do you think these house plans would be useful to an architect or a builder?
VIDEO: House Plans
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore building plans and consider how geometry and measurement are important to people such as architects and builders.
Opening
Explore how geometry and measurement are important to architects and builders.
House Plans
Preparing for Ways of Thinking
Monitor students as they work, making sure that they are interpreting the plans correctly. Ask questions to prompt students’ thinking.
- Students who point out flaws in the house floor plan when comparing it to a human scale (the kitchen is very small—smaller than the bathroom; one bedroom is narrow but workable; the dining room and living room locations should probably be switched)
SWD: Some students may need additional prompting and scaffolding to interpret the plans. It may be helpful to model for students how one can make observations using information presented in the plans (e.g., key, legend, scale). Then support students as they complete guided practice with this skill. Determine which partnerships and configurations best support all students’ learning. You may decide to group or partner students with similar abilities (to allow for teacher support) or group them heterogeneously to promote cooperative learning. Students with disabilities may benefit from working alongside typically developing peers who are able to provide ongoing modeling of skills and strategies.
ELL: Most students from countries outside the United States are used to the metric system. If some students are having trouble with the measurements “foot” and “feet,” explain the history around the origin of those words. It used to be the case that people measured with their foot. Additionally, be sure students understand that “feet” is the plural of “foot” (it is an irregular plural), and ask them to find similar examples such as “tooth” and “teeth.”
ELL: When eliciting answers, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a foreign language. For example, if you hear students say the right things but with the wrong grammatical structure, show signs of agreement and softly point to the correct grammar, using the student’s words as much as possible. For example, in this task, if the students says “36 long and 22 across, and then 792 total,” nod and say something along the lines of, “Exactly, the house is 36 feet long and 22 feet wide. The area is 792 square feet.” (Words in bold should be spoken slowly and sometimes repeated by the student who stated the answer—and other students as appropriate).
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
- Look for students who see the connection between the measurements and human scale, understanding what the quantities mean in context.
Mathematical Practice 5: Use appropriate tools strategically.
- Look for students who use a scale to determine the measurements and the size of a person to determine the scale.
Mathematical Practice 6: Attend to precision.
- Look for students who identify units when discussing the numbers and who use the correct units (feet versus square feet versus cubic feet)—a very important aspect to measurement at this level.
Possible Answers
- The house is 36 ft long and 22 ft wide and has an area of 792 sq ft. (Remind students how to find area.)
- The kitchen window is about 2 ft from the side of the house and about 2 ft above the ground. It would use about 12 sq ft of glass.
Lists will vary.
Students may notice that the front door is 5 ft tall and approximately 2 ft wide, the hallways are 2 ft wide, and the doors to each room are 2 ft wide. These measurements are unreasonable because it would be difficult for people to walk around in the house. In addition, the height of the house varies by approximately 1 ft when comparing the front and side elevations. The wall thickness also varies as you compare the front and side walls of the house.
Work Time
House Plans
What measurements could you determine based on the house plans?
For example:
- How long is the house? How wide is the house? How much floor space does the house have?
- How far is the kitchen window from the side of the house? How far above the ground is the kitchen window? How much glass is needed for the window?
- Make a list of some other measurements that you could determine based on the house plans. (You do not need to calculate the answers.)
- After examining the video, are there any measurements that are unreasonable or inaccurate in the house? Provide evidence and explain why.
VIDEO: House Plans
Hint:
- What types of measurements besides length can you determine based on the plans?
Building Plans
Preparing for Ways of Thinking
Look for students who find unusual measurements, such as the wall thickness (about 1 ft) or roof height (12 ft). Some students may look at the interior dimensions to determine the length of the house. Is it 36 ft long (outside) or about 34 ft long (inside)?
In addition, provide sentence frames in anticipation of the answers students might provide. For example:
- To find these costs, the builder would need to….
- The price of the items would be calculated….
Use sentence frames to help scaffold other responses.
Interventions
Student does not see volume as an option for measuring.
- How could you find how much air would be inside the house?
- How much space would the air take up?
Student does not think of area as a measurement.
- How would you decide how much carpet costs? How much area does it cover?
- How would you compare the amount of carpet needed for each room?
Possible Answers
- To find any of these costs, the builder would need to calculate area (for outside paint, the lateral surface area). Each of these items would be priced by cost per square foot.
- The air takes up all the space inside of the house, i.e., its volume. Heating and air conditioning costs would be priced per cubic foot. The volume could be found by multiplying the length (36 ft) by the width (22 ft) by the height (about 7 ft), which is 5,544 cu ft.
- The builder needs to know specific dimensions to locate things correctly. In fact, the drawings are considered a contract between the architect and the builder (often called a contractor).
Work Time
Building Plans
Think about why being able to determine measurements like the ones you just listed would be important to an architect or builder.
- How could a builder use such measurements to determine the costs of carpet, window glass, or paint for the outside of the house?
- How could a builder use such measurements to determine heating or air conditioning costs?
- Why would an architect need to know the exact location of a window or door when drawing up plans for an addition to a house?
Pantheon
Lesson Guide
Students should be focusing on the strategies they used to approximate the height and width of the building.
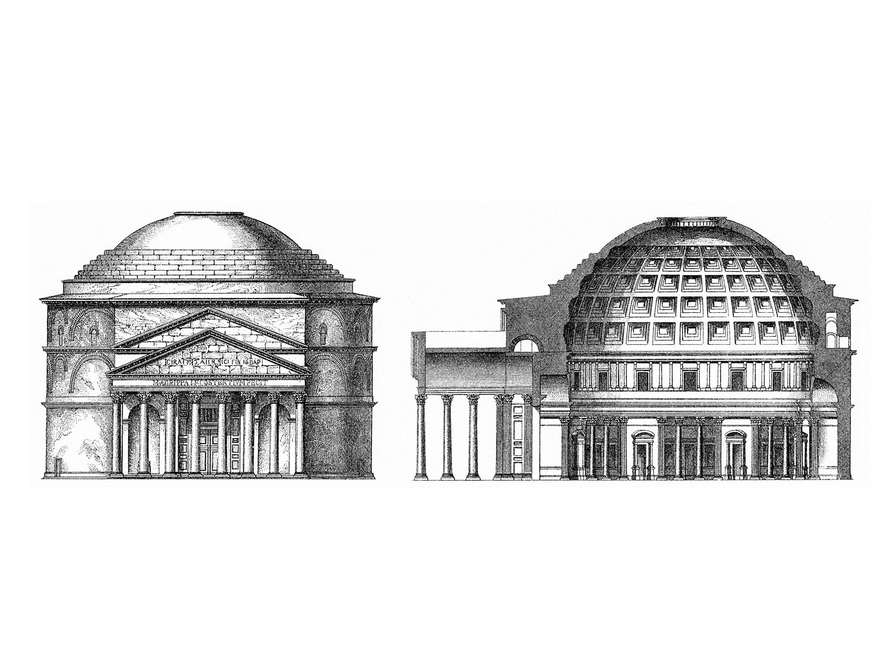
This picture shows the building plans of a famous building in Rome called the Pantheon. The plans also show a “vertical slice” that reveals the inside of the building; notice the domed ceiling.
- How tall and how wide do you think the building is? Explain.
Preparing for Ways of Thinking
Look for students who have sense of scale and respond in ways similar to these:
- Students who explain they found the height of the Pantheon by using the scale of one person to find the number of people that could be stacked vertically beside the building
- Students who notice that the height of the Pantheon is equal to its width (a sphere would fit inside the building)
SWD: Prior to the Ways of Thinking discussion, circulate and check in with students. You may want to preview the questions that will be discussed with students who may need additional time to process the information.
Possible Answers
- Answers will vary.
- Students have nothing to compare the building with to get a sense of scale. The stairs offer a clue as to the dimensions, but the steps are actually fairly large, which makes the user feel smaller still. (The Pantheon is approximately 142 ft tall and 243 ft wide.)
- Student strategies will vary.
Work Time
Pantheon
This picture shows the building plans of a famous building in Rome called the Pantheon. The plans also show a “vertical slice” that reveals the inside of the building; notice the domed ceiling.
- How tall and how wide do you think the building is?
- Explain and justify the thought process you used to determine the height and width of the building.
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- What measurements did you find other than the ones mentioned in the questions?
- How did you determine these measurements?
- Why do you think the roof is sloped? (To shed snow and rain.)
- How could you describe the location of the front bedroom door? (It is about 12 ft into the house and 16–18 ft to the right down the hallway.)
- How did you determine the height and width of the Pantheon?
- If a person were as tall as the Pantheon columns, what do you think the dimensions of the building would be?
- How thick do you think the walls of the Pantheon are? Why are they so thick? (The walls are several feet thick to support the dome.)
- Why do you think the building is so tall? ( To make people feel small and insignificant and in awe of the power it represented as the building was a temple to the ancient Roman gods.)
ELL: The word sloped is widely used in statistics, but some ELLs might not be familiar with its use in everyday life. Consider showing a picture of a sloped roof and ask a few questions to confirm that ELLs have absorbed the new vocabulary. Introduce the noun slope and explain that sloped is the corresponding adjective.
Performance Task
Ways of Thinking: Make Connections
Take notes about other students’ ideas concerning the types of measurements that can be determined from building plans and why being able to make such determinations is useful.
Hint:
As your classmates present, ask questions such as:
- What measurements did you come up with?
- How did you determine these measurements?
- Why do you think the roof is sloped?
- Can you describe the location of the front bedroom door?
- How did you determine the height and width of the Pantheon?
- If the height of the columns of the Pantheon were equivalent to the height of an average person, what do you think the approximate dimensions of the building would be?
- How thick are the walls of the Pantheon? How can you tell? Why do you think the walls are so thick?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see how students think about applying geometry to read architectural floor plans. If you notice any insightful comments, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about showing three-dimensional buildings in two dimensions is…