- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Exploring Cross-Sections

Overview
Students will explore the cross-sections that result when a plane cuts through a rectangular prism or pyramid. Students will also see examples of cross-section cuts in real-world situations.
Key Concepts
Students are very familiar with rectangular prisms, and to a lesser degree, they are familiar with rectangular pyramids. However, students haven’t been exposed to the myriad possibilities for solids that result from planar slices. The purpose of the lesson is for students to explore these possibilities.
Goals
- Identify the plane figures that result from a plane cutting through a rectangular prism or pyramid.
Explore the Effects of Slicing Through Solids
Lesson Guide
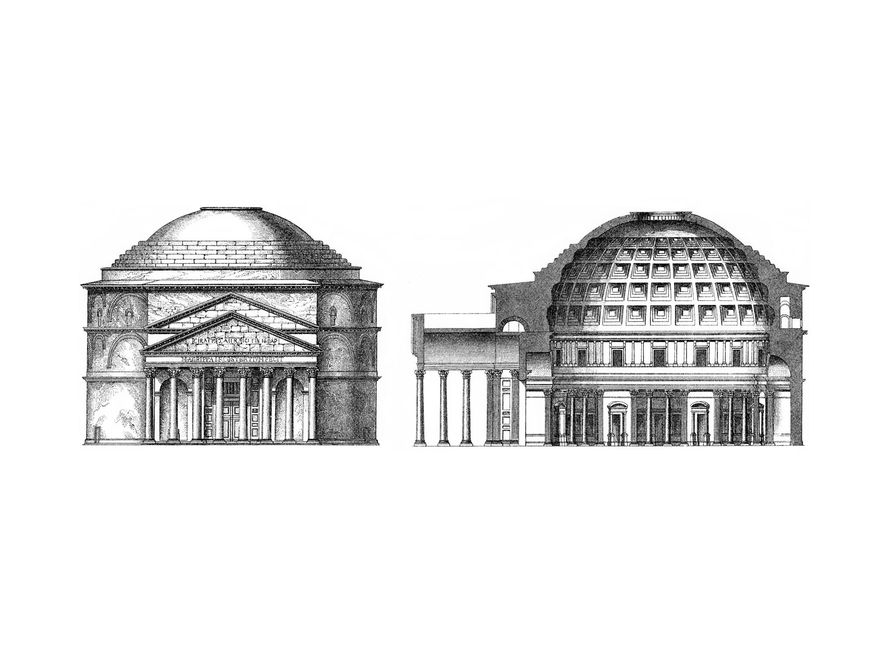
Show students the image of the Pantheon and its cross section. Discuss the question about where students think the cut for the pyramid was made.
Mathematics
The cut for the pyramid was taken perpendicular to the base and parallel to two sides, directly through the apex. The cut must be through the apex because the cross section is a triangle, not a trapezoid. (Actually, the image shows a trapezoid because the capstone is missing, but students could argue that the cut is just in front of or behind the apex.)
Opening
Explore the Effects of Slicing Through Solids
Cuts through buildings result in views called cross sections. Cross sections are used to show the details and structure of the inside of a building. (A floor plan is actually a slice through a building made a few feet above the ground.)
This cross section of the Pantheon shows the dome inside the building.
Look at the cross section of the pyramid.
- Where do you think the cut for the pyramid was made? Explain.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore the cross sections that result from slicing through a rectangular prism or pyramid.
Opening
Explore the cross sections that result from slicing through a rectangular prism or pyramid.
Slicing Through Prisms
Lesson Guide
Spend time prior to the lesson using the interactive and finding the different cross sections.
Have students work in pairs. Give students some time to get familiar with the interactive before moving on to the tasks. They need to see how the interactive works and have some time to experiment.
Make sure students understand how to use the interactive as they explore.
Mathematics
Students will discover several things as they explore. They will see that some cuts produce surfaces similar or congruent to the base or side (in the case of the rectangular prism). Cuts that are parallel generally produce surfaces that are similar to one another (such as an isosceles triangle).
SWD: Students with disabilities may need additional time to learn how to use the tool. If possible, give them a chance to preview the tool prior to class.
Check to make sure that students have a clear sense of the tasks they need to be able to accomplish using the interactive. It may be necessary to model several possible cuts for students who struggle with mathematical understanding to show them variations. Demonstrate for students one possible cut and prompt students to show you another.
It may be helpful to print out basic directions for the interactive, so that students can refer to a paper resource as they develop proficiency with the interactive on their devices.
SWD: Students with visual-spatial vulnerabilities may struggle to recognize the relationships between and among shapes and slices of shapes. Direct instruction and explanation of this concept may be necessary.
ELL: When discussing topics or giving instructions orally, allow time for students to preview the academic vocabulary ahead of time. Examples of academic vocabulary terms to preview are congruent, parallel, base, surface, side, and isosceles. Write the terms on the whiteboard or project definitions. Allow ELLs, and all students, to use a dictionary if they wish.
ELL: Consider allowing ELLs to write up parts of their answers. Sometimes it is hard for ELLs to explain the whole phrase, but they can skillfully either draw what they mean or show a graph or a picture. This applies to all of the answers.
SWD: Students may benefit from scaffolding questions such as:
- How are certain cuts similar?
- How are they different?
- What is the relationship between cuts that run parallel to each other?
Interventions
Student has difficulty getting started.
- How does the surface compare to the base or a side of the rectangular prism?
- If the height were 6 cm, how would the volume change?
Student does not see other possible cuts.
- What happens if the cut is perpendicular to the base but not parallel to a side?
- What happens if the cut is not perpendicular to the base?
Student has a solution.
- Can you make a cut that would be just one point?
- Can you make a cut that would be a line segment?
Student does not see how the slices are made.
- If you had a stick of butter and cut it with a knife, what could the surface of the slice look like?
- How are the slices in a loaf of bread like the cuts parallel to the base of a rectangular prism?
Mathematical Practices
Mathematical Practice 1: Make Sense of Problems and Persevere in Solving Them
Students will be exploring and discovering different things as they work through the problems and use the interactive.
Mathematical Practice 2: Reason Abstractly and Quantitatively
Some students will make connections to the previous lesson and realize that some of the conclusions about slices through a rectangular prism would apply to all prisms (such as cuts parallel to the base being congruent).
Mathematical Practice 6: Attend to Precision
Look for students who use the interactive systematically to establish patterns and draw conclusions.
Mathematical Practice 7: Look For and Make Use of Structure
Some students will again make the connection between 2-D measurement and its application here. Things that they learned about finding the area of polygons, and scale, would apply here, except that calculating the area of cut surfaces would be difficult.
Possible Answers
- The cross sections are congruent to the base. This reinforces the idea of volume, as each cut is like a congruent layer of the prism.
- The cross sections will all be rectangles.
- To produce isosceles or equilateral triangle cross sections, the cuts will not be perpendicular or parallel to the base or side. The slices need to be diagonal so that one end of the plane does not reach two opposite sides, but cuts through an edge to produce a vertex. The One World Trade Center building is an example of architecture in which slices produce isosceles triangles.
Different cuts can produce cross sections that are congruent to the base, a side, or even triangles if the cut is through the corner of a prism.
A slice that is not parallel to the base and contains points from the four vertical edges of the prism reveals a parallelogram. Even slices that are parallel to the base of a rectangular prism can reveal a cross section that is a parallelogram, as a rectangle is considered a parallelogram.
Work Time
Slicing Through Prisms
Use the interactive to explore what happens to solids when you slice through them in different ways. When you slice through a 3-D object, the surface formed is called a cross section.
- For a prism, what shape(s) is the cross section that is formed by making a slice parallel to the base?
- What shape(s) would be formed by making a slice perpendicular to the base?
- Is there a way that you can slice through a rectangular prism to reveal an isosceles triangle or an equilateral triangle?
- What do you notice?
- Is there a way that you can slice through a rectangular prism to reveal a cross section that is a parallelogram?
INTERACTIVE: Slicing through Solids
Hint:
- What is similar about the cross sections that result from each type of slice?
Slicing Through Pyramids
Lesson Guide
Have students work in pairs. Give students some time to get familiar with the interactive before moving on to the tasks. They need to see how the interactive works and have some time to experiment, so they understand how to make the desired cross sections.
Check to make sure that students have a clear sense of the tasks they need to be able to accomplish using the interactive. It may be necessary to model several possible cuts for students who struggle with mathematical understanding to show them variations. Demonstrate for students one possible cut and prompt students to show you another.
It may be helpful to print out basic directions for the interactive so that students can refer to a paper resource as they develop proficiency with the interactive on their devices.
Interventions
Student has difficulty getting started.
- How does the cut parallel to the pyramid base compare to the base?
Possible Answers
- The cross sections are similar to the base.
- For a rectangular or square pyramid: Cross sections formed by slicing perpendicular to the base and through two adjacent edges of the base will be triangles (this includes the cross section that cuts through the apex). Cross sections formed by slicing perpendicular to the base through two opposite sides of the base, and not through the apex, will be trapezoids.
- For a square pyramid: Isosceles triangle cross sections can be formed by slicing through the apex and two opposite vertices of the base (triangular cross sections parallel to this will also be isosceles); it is also possible to make isosceles cross sections without slicing perpendicular to the base. Depending on the dimensions of the pyramid, it may only be possible to make an equilateral triangle cross section with a slice that is not perpendicular to the base.
- It is possible to cut similar shapes without slicing perpendicular to the base. It is also possible to make trapezoid and triangle cross sections that are parallel; the cross section shape will change from a trapezoid to a triangle when the slice intersects the apex.
- A slice that is parallel to the base will reveal a cross section that is a square or rectangle.
Work Time
Slicing Through Pyramids
- For a rectangular or square pyramid, what shape(s) is the cross section that is formed by making a slice parallel to the base?
- What shape(s) could the cross section be when making a slice perpendicular to the base?
- Is there a way to slice through the pyramid to reveal an isosceles triangle or an equilateral triangle?
- What do you notice?
- Is there a way to slice through the pyramid to reveal a cross section that is a parallelogram?
INTERACTIVE: Slicing through Solids
Explore the Effects of Slicing Through Solids
Possible Answers
Citigroup Center: rectangular prism
John Hancock Center: rectangular pyramid
Shanghai World Financial Center: square prism
Transamerica building: combination of a square pyramid and a rectangular prism
Citigroup Center: This is a rectangular prism that has been sliced diagonally.
John Hancock Center: This is a very tall rectangular pyramid that has been sliced off parallel to the base.
Shanghai World Financial Center: This building is similar to the One World Trade Center building. It is based on a square prism that is sliced through the diagonal of the top base down to a vertex of the bottom base, on both sides.
Transamerica building: This building is a little different because it’s really a combination of two solids—a square pyramid with a narrow rectangular prism intersecting it. (Note: Its official name is the Transamerica Pyramid, but it was changed in the lesson so as to not reveal the answer.)
Work Time
Explore the Effects of Slicing Through Solids
These images show four well-known buildings from around the world: the Citigroup Center in New York City, the John Hancock Center in Chicago, the Shanghai World Financial Center, and the Transamerica building in San Francisco.
- What solid do you think each building is based on?
- How was the solid sliced to produce the shape of the building?
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who demonstrate the following strategies during the class discussion:
- See the relationship between slices that are parallel to a rectangular prism base and the volume of those prisms (that each slice is congruent to the base and similar to the layers of a prism).
- See the similarity between cross sections and their bases (such as a slice that is parallel to the pyramid base).
- See different or unusual slices and their cross sections (such as a slice of a rectangular prism that produces a trapezoid or parallelogram cross section).
- See that cross sections will have different characteristics if the base of the solid is a square (such as an isosceles triangle cross section versus a scalene triangle cross section for slices parallel to the diagonals in a pyramid).
- Find that a pentagon or a hexagon cross section is possible from a slice of a rectangular prism, and a pentagon cross section is possible from a slice of a rectangular pyramid.
Possible Answers
Presentations will vary.
Challenge Problem
Possible Answers
- The largest equilateral triangle has its vertices at the three vertices of the cube that are diagonal from each other. If students made the cube from the Gallery problem “Parallelogram to Cube” in Unit 7.3, they will see this shape after three parallelograms are fitted together.
Work Time
Prepare a Presentation
Describe the shapes you get from slicing a rectangular prism and a rectangular pyramid. Use your work to support your explanation.
Challenge Problem
- What is the largest equilateral triangle cross section that can be made by slicing through a cube?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- What shapes were you able to find for the cross sections?
- Could you make a slice that would produce only a point or a line segment cross section? How?
- What do parallel slices have in common?
- If the base for either solid was square, how would that affect the cross sections?
- Is it possible to have a cross section with more than four sides? How?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of mathematics?
- How did [student name] make sense of the problem?
- Could you state what [student names] said in a different way?
- How would you measure the lengths of the sides of a cross section?
- Can you think of other things in daily life that are sliced, (e.g. bread, cheese, meat)?
ELL: When giving directions for this discussion, be sure that students understand that they can complement their oral explanation with graphs, pictures, and drawings. Provide a few sentence frames that you think ELLs might need.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ explanations and understandings of slicing through solids.
Hint:
As your classmates present, ask questions such as:
- What do the results of the parallel slices have in common?
- What do you notice about the cross sections that result from slicing through solids with square bases?
- Could you make a slice that would produce only a point or a line segment? How?
- Is it possible for a cut to result in a cross section that has more than four sides? Explain how.
Slicing Through Solids
A Possible Summary
- If a plane intersects a solid, the intersection creates 2-D cross sections (a point, a line segment, or a plane). The cross sections are often congruent or similar to the base of the solid (rectangular prisms and pyramids). Many cross sections can be produced, including rectangles, trapezoids, and isosceles triangles.
Formative Assessment
Summary of the Math: Slicing Through Solids
- Write a summary about slicing solids.
Hint:
Check your summary:
- Do you explain, in terms of geometry, how a cross section is made by slicing through a solid?
- Do you explain how some cuts through a rectangular prism are similar to the base or sides of the prism?
- Do you describe which plane figures can be made by slicing through rectangular prisms or pyramids?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see what students think about the cross sections that result from slicing through a rectangular prism or pyramid. If you notice insightful comments about students’ explorations of cross sections, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some places where I have seen solids that have been sliced are …