- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Shape Animation 2
Applying The Volume Formula

Overview
Students discover the formula for finding the volume of a pyramid and apply the formula to solve problems.
Key Concepts
The volume of a pyramid is one-third the volume of a prism with the same base and height. The shape of the base does not matter (including if it’s a circle), and students will see the same one-third comparison between a cylinder and cone.
Goals
- Understand the formula for the volume of a pyramid.
- Apply the volume formula to solve problems.
Shape Animation
Lesson Guide
Show students the video and preface it by asking them to think about what it says about the volume of a pyramid.
Mathematics
Briefly discuss students' ideas about the video. Ask students how the volume of the pyramid compares to the volume of the cube.
ELL: Before starting the discussion, ask students if they understood the video. Check that the ELLs were able to follow it and the foundations of the topic presented in it. Offer to play it one more time, pausing when necessary, if some ELLs struggled to follow it.
Opening
Shape Animation
Watch this video.
- What does this video show?
- What can you say about the volume of a pyramid based on the video?
VIDEO: Shape Animation 1
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore and apply the formula for finding the volume of a right rectangular pyramid.
Opening
Explore and apply the formula for finding the volume of a right rectangular pyramid.
Find Volumes of Right Pyramids
Lesson Guide
Have students work with a partner. Make sure that students are clear on how to find the volume of a pyramid before they move on to solving the problems.
ELL: As you listen to the answers, you may want to ask ELLs to write up what they are saying. Sometimes it is hard for ELLs to explain the whole phrase, but they can skillfully either draw what they mean, show a formula, or do something else in writing. This approach applies to all of the answers.
SWD: Partner work provides students with disabilities with numerous opportunities to collaboratively interact with the mathematics as they share ideas, strategies, and solutions.
Interventions
Student has trouble seeing the formula.
- How many times was the pyramid emptied into the prism?
- So, what fraction of the cube’s volume is the pyramid’s volume?
- How do you find the volume of a prism?
- Then, how would you find the volume of a pyramid with the same dimensions?
Student has a solution.
- How many times larger is the prism’s volume compared to the pyramid’s volume?
- How does the density of the material in the pyramid affect its volume? (It doesn’t, but it does affect its weight.)
Student does not think that the volume of the pyramid will always be one-third of the prism.
- Construct your own pyramid and prism of any base or height and see if three pyramids fill the prism. (Make the figures out of paper and use something light to fill them, such as rice or corn kernels or popcorn!)
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Look for students who see that a prism with the same base and height as a pyramid will have three times the volume.
Look for students who realize that the rectangular prism problem has many solutions, including altering the prism.
Mathematical Practice 4: Model with mathematics.
Some students will realize that volume does not need to be calculated to find the dimensions of a rectangular pyramid that has the same volume as a prism with known measurements.
Some students will realize that they can take one-third of one of the dimensions before multiplying, rather than after multiplying (especially if one dimension is a multiple of 3).
Possible Answers
- The video demonstrates that the volume of the pyramid is one-third of the volume of the prism (or that the prism’s volume is three times the pyramid’s volume).
- The prior video demonstrates the same principle, but it does so by combining the pyramids.
- Yes, if the prism and pyramid measurements differed from one another, the results would be different.
- As long as the bases and heights of the prism and the pyramid match, the results will be the same.
- When finding the volume of a prism, find the area of the base and then multiply by the height of the prism. For a right pyramid, find the area of the base and multiply by the height of they right pyramid. Then multiply by because it takes the volume of three pyramids to equal one prism that has the same base and height.
Work Time
Find Volumes of Right Pyramids
Watch the video.
- What does the video demonstrate?
- How does the video relate to the video you just watched?
- If the pyramid and cube had different heights or widths from each other, do you think the results would be different?
- If the base of the prism had a different shape, do you think the results would be different?
- Explain the difference between finding the volume of a prism and finding the volume of a right pyramid. Provide rationale.
VIDEO: Shape Animation 2
Find Volumes of Rectangular Right Pyramids
Lesson Guide
By the end of this task, make sure students are clear on the formula for finding the volume of a pyramid before they move on to solving the problems in this task and the next task. Students will continue to work in pairs for the rest of the volume problems.
Possible Answers
- The volume of a prism can be found using V = Bh.
- The volume of a prism can be found using V = Bh.
For a right rectangular pyramid with a height of 8 in. and a base of 5 in. by 6 in.:
V = (5 ⋅ 6)8
V = (30)8
V = (240)
V = 80 or 80 in
Work Time
Find Volumes of Rectangular Right Pyramids
- What is the formula for the volume of a prism (with any type of base)?
- Use this formula, as well as what you learned from the video, to determine the formula for the volume of a right rectangular pyramid.
- What is the volume of a right rectangular pyramid that has a height of 8 in and a base that is 5 in long and 6 in wide?
Find the Volume of the Great Pyramid in Egypt
ELL: Be sure to define approximation. Explain that in solving math problems, we sometimes look for answers that are precise while other times an approximation is sufficient. The context of the problem determines whether the answer should be precise or an approximation.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
- A calculator would be a useful tool to find the volume of the Great Pyramid, as long as students have an idea of how large the number will be.
Mathematical Practice 6: Attend to precision.
- Students should see that the volume of the Great Pyramid is at best an approximation (the dimensions are also given as an approximation), and that the answer will not be precise.
- Look for students who use the correct units for the answers (cubic units).
Possible Answers
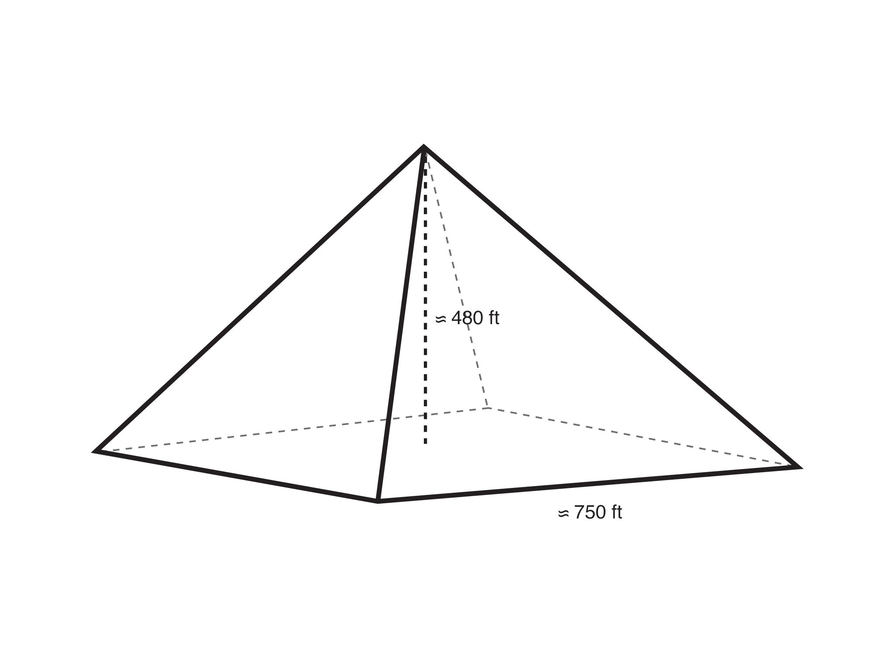
V = Bh
The volume is 90 million ft.
V= (750 ⋅ 750)480
V = (750 ⋅ 750)160
V = (562,500)160
V = 90,000,000 or 90,000,000 ft
Work Time
Find the Volume of the Great Pyramid in Egypt
The Great Pyramid in Egypt is about 480 ft high. It has a square base with side lengths of about 750 ft.
- What is the volume of the pyramid?

Find Dimensions of Pyramids Given the Volume
Possible Answers
- With the dimensions the same for each figure, the pyramid will have one-third the volume. So, one of the dimensions must be three times larger for the volumes to be equal. The volume of the prism would be 72 cm.
Pyramid height: 27 cm (9 ⋅ 3 = 27)
Pyramid base width: 4 cm
Pyramid base length: 2 cm
OR
Pyramid height: 9 cm
Pyramid base width: 12 cm (4 ⋅ 3 = 12)
Pyramid base length: 2 cm
OR
Pyramid height: 9 cm
Pyramid base width: 4 cm
Pyramid base length: 6 cm (2 ⋅ 3 = 6)
- Some students might look at the prism and make its height 3 times less, or 3 cm (9 ÷ 3 = 3), but otherwise have the same dimensions for both figures.
Work Time
Find Dimensions of Pyramids Given the Volume
A rectangular prism has a height of 9 cm, a width of 4 cm, and a length of 2 cm.
- Find the dimensions of a rectangular pyramid that has the same volume as the prism.
- Can you find more than one solution?
Hint:
- How does the volume of a prism compare to the volume of a pyramid that has the same base and height?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to be shared during the class discussion:
- Students who use different dimensions to solve the rectangular prism problem
- Students who also realize that the prism could be one-third of the height of the pyramid (rather than having the pyramid’s volume match the prism’s volume)
- Students who make the connection to prisms, where the shape of the base does not matter in finding the volume, just as it doesn’t with pyramids
Possible Answers
Presentations will vary.
Challenge Problem
Possible Answers
- If the plastic in the toy is 1.2 grams per cubic centimeter, then the volume of the pyramid is about 41.7 cm ( 50 g ÷ 1.2 g/cm = 41.7 cm).
The area of the base is 25 cm (5 cm • 5 cm), so the formula can be used to solve for the height.
V = Bh
41.7 = () (25)h
125 = (25)h
5 = h
So, the pyramid will be 5 cm in height.
Work Time
Prepare a Presentation
Explain what you know about finding the volume of right pyramids. Use examples of your work to illustrate your explanation.
Challenge Problem
A toy company wants to make a solid square pyramid toy. The base of the toy will have side lengths of 5 cm, and the toy will weigh 50 g.
- If the plastic in the toy weighs 1.2 g per cm, what will the height of the toy be?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work.
Ask questions such as these:
- How accurate do you think your answer is for the volume of the Great Pyramid? Why?
- How did you calculate the volume of the pyramids?
- What strategies did you use to equalize the volume of the pyramid and prism in the rectangular prism problem?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- How is density related to volume?
SWD: Provide a safe setting for students with disabilities to ask questions about any misconceptions they may have. Help students break problems down by thinking aloud and asking questions that get them to think about the mathematics behind the problem.
ELL: As students present their solutions, make connections between different solutions to the same problem so that students can see the multiple ways to solve a problem.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ explanations for finding the volume of right pyramids.
Hint:
As your classmates present, ask questions such as:
- How did you use the formula for the volume of a prism to find the formula for the volume of a pyramid?
- How did you calculate the volume of the pyramid?
- What strategies did you use to make the volume of the pyramid and prism equal?
- How accurate do you think your answer for the volume of the Great Pyramid is? Explain your reasoning.
Volumes of Right Pyramids
A Possible Summary
- The volume of a pyramid is one-third the volume of a prism with the same base and height, regardless of the shape of the base. The formula for the volume of a pyramid is V = Bh.
Formative Assessment
Summary of the Math: Volumes of Right Pyramids
Write a summary about finding the volumes of right pyramids.
Hint:
Check your summary:
- Do you discuss how the volume of a pyramid compares to the volume of a prism with the same base and height?
- Do you explain how to find the volume of a pyramid?
- Do you provide the formula for the volume of a pyramid, and explain the formula?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see how students think about finding the volume of a right pyramid. If you notice insightful comments about how to explore and apply the formula for finding the volume of a right pyramid, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some examples of pyramid shapes that I have seen outside of the classroom are …