Polygons

Overview
Students find the area of regular polygons, recalling what they already know about the area of geometric shapes and generalizing a formula for any regular polygon.
Key Concepts
Students will recall what they already know about the area of geometric shapes and apply that to find the area of regular polygons. Any regular polygon can be divided into congruent isosceles triangles. If the length from the center to the midpoint of a side (the apothem) is known, the area of the triangles and the area of the polygon can be found. Students will see the similarities between the area of a polygon and derive the formula for the area of a circle.
Goals
- Review area of triangles, rectangles, and parallelograms.
- Find the area of regular polygons.
- Generalize an area formula for any regular polygon.
ELL: This lesson offers students a rich opportunity to learn academic vocabulary. Display the new terms in writing somewhere visible in the classroom so that you can refer to them. Allow ELLs to use their bilingual dictionaries to help with understanding the terms. When possible, have ELLs discuss the terms in their language of choice with other ELLs who share the same primary language.
Area of an Octagon
Lesson Guide
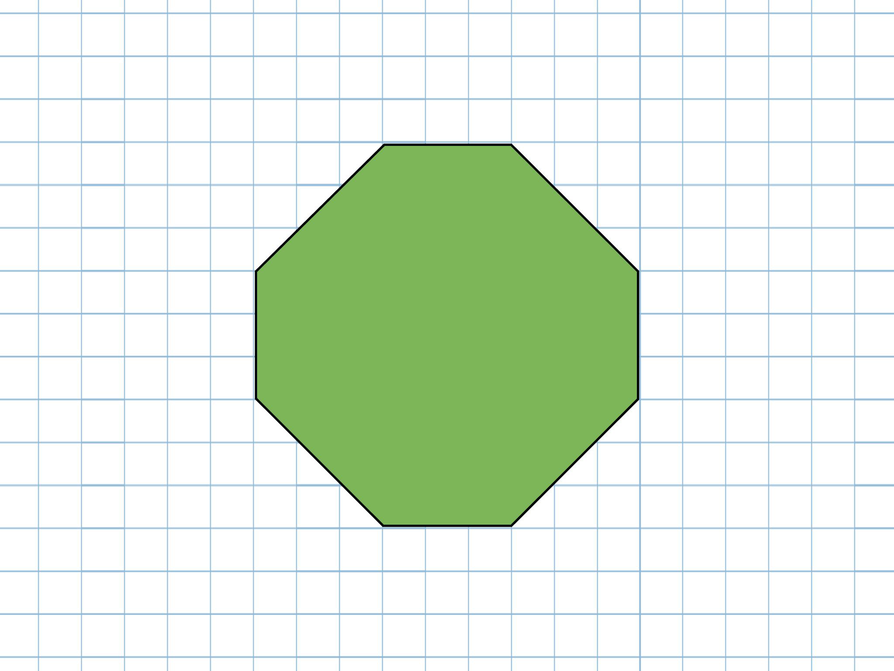
Show students the octagon and read aloud the question, “How can you find the area of this octagon?”
Mathematics
Briefly discuss the opening question, taking a few suggestions. Students will see that the octagon can be divided into figures for which they know the area. There are several ways to divide the figure. Make sure to discuss these ideas:
- The area of a rectangle or parallelogram is length multiplied by width (or base multiplied by height): A = lw or A = bh
- The area of a triangle is the base multiplied by the height, divided by 2, or one-half the product of the base and the height: A = bh
- Is the octagon regular? (Answer: No, the sides are not all congruent.)
ELL: Students with language-based learning disabilities may struggle to retain and recall the meaning of number prefixes such as oct. It may be helpful to review these prefixes with students or provide a chart with the prefixes and their numerical meanings.
When teaching students numerical prefixes, it may be helpful to provide examples of words that include that prefix along with images that represent the words; for example, octopus. This technique will support student comprehension and recall of these prefixes.
If you are having students compile a list or resource with key vocabulary terms for this unit, this may be a good time to have them add these words to their resource.
SWD: Check in to ensure that students understand the meaning of domain-specific vocabulary terms such as regular, congruent, isosceles, parallelogram, apothem, vertex, radius, prism, right prism, polygon, base, scale, and net.
Opening
Area of an Octagon
How can you find the area of this octagon?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find the area of regular polygons.
Opening
Find the area of regular polygons.
Find the Area of Regular Polygons
Lesson Guide
Have rulers ready for students to use, as well as printed copies of the polygons.
Make sure students spend time discussing the first task. Ask them prompting questions to see if they have thought about the problem and to guide them toward a solution.
Examples for critiques would be: “I don’t quite understand how you came to the conclusion that… because…,” or “Please explain to me how you came to that conclusion since I can't see it myself.”
ELL: When prompting responses from ELLs, be sure to listen closely since they might not be using the right grammatical structure. For example, if they say, “Polygons are divided into triangles,” agree with them, and further explain that polygons can be divided, and so on. Also, ask questions to get more accurate responses. An example of a probing question might be, “What type of triangle?” If they can show it but don't say the word, further ask, “What is the word we use to talk about that type of triangle?”
ELL: Consider providing ELLs with sentence frames to support them in building arguments and critiquing. Examples would be: “I think that the area of this polygon is … because…” or “My reasoning behind the formula is…."
SWD: Students with visual-spatial reasoning challenges may have trouble identifying the sub-shapes that make up the polygons. In this case, it may be helpful to model for students how to divide the octagon into congruent isosceles triangles. Then have students divide the hexagon into congruent isosceles triangles during guided practice.
- Providing a tactile manipulative will help students to better understand the relationships between the triangles and the polygons.
- Showing students one of the visuals, the trapezoid or the rectangle, may help them to see how the shape might be reconfigured. Students with visual-spatial vulnerabilities may not be able to make this step independently.
ELL: If students use the wrong grammatical structure, such as, “The polygons have congruent isosceles triangles. We measure height and base,” nod and say something like, “Exactly. The polygons can be divided into congruent isosceles triangles. The measurements are the base and the height.” (Words in bold can be uttered more slowly and repeated by the student who uttered the answer—and by other students as appropriate).
Interventions
Student has difficulty getting started.
- What measurements do you know about the polygon?
- Can you use those to find the area of a figure in the polygon?
- What is true about the side lengths of a regular polygon?
- If a regular polygon has 20 sides, how can you find its area? What information do you need?
Student thinks that all polygons are regular and/or that the formula would apply to any polygon.
- Can you draw a figure with 6 sides? Are the lengths of each side the same?
- If you divide the hexagon into 6 triangles, would they all be the same?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Look for students who work out how to find the area prior to cutting the polygons into figures they know how to find the area for.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Some students will explain and defend their reasoning in generalizing the area formula.
Mathematical Practice 5: Use appropriate tools strategically.
- Some students may not need to cut the polygons into triangles to see the pattern in finding the area, but for many students, this will be a very useful step (and will help when the area of a circle is discussed in a later lesson).
Mathematical Practice 6: Attend to precision.
- Look for students who use the term apothem correctly and understand its meaning in relation to the polygon. Also look for students who label units and label units correctly (centimeters for length and square centimeters for area).
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Students work through the process of finding patterns and similarity between the figures, as they move toward a general formula.
Possible Answers
Choices may vary.
- The polygons can be divided into congruent isosceles triangles (with given measurements being the base and height). The area of each polygon can be found by multiplying the area of the triangle by the number of sides:
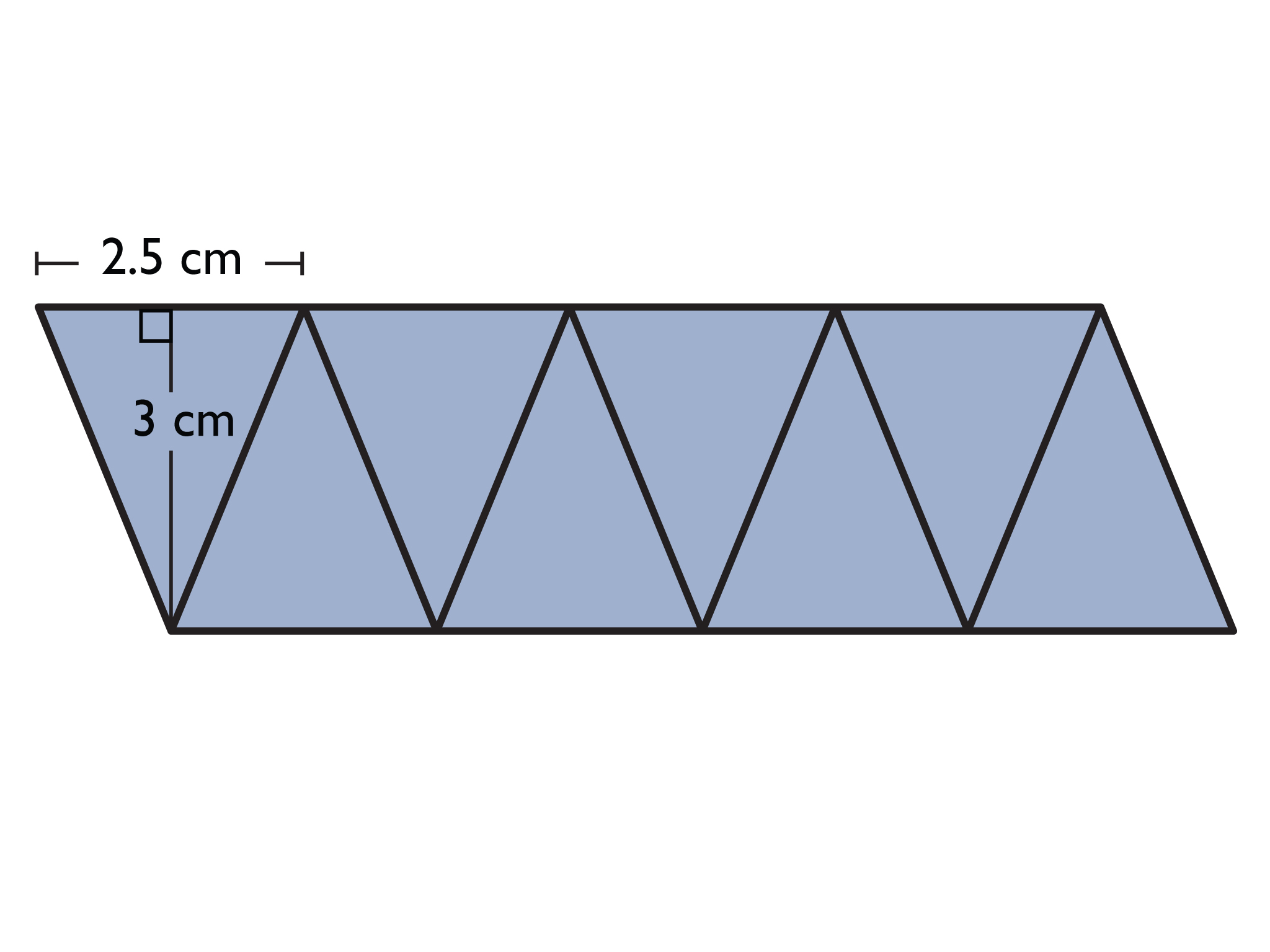
Octagon
Area of one triangle = 12(2.5)(3) = 3.75
Area of octagon = 3.75 ⋅ 8 = 30
The area of the octagon is 30 square centimeters.
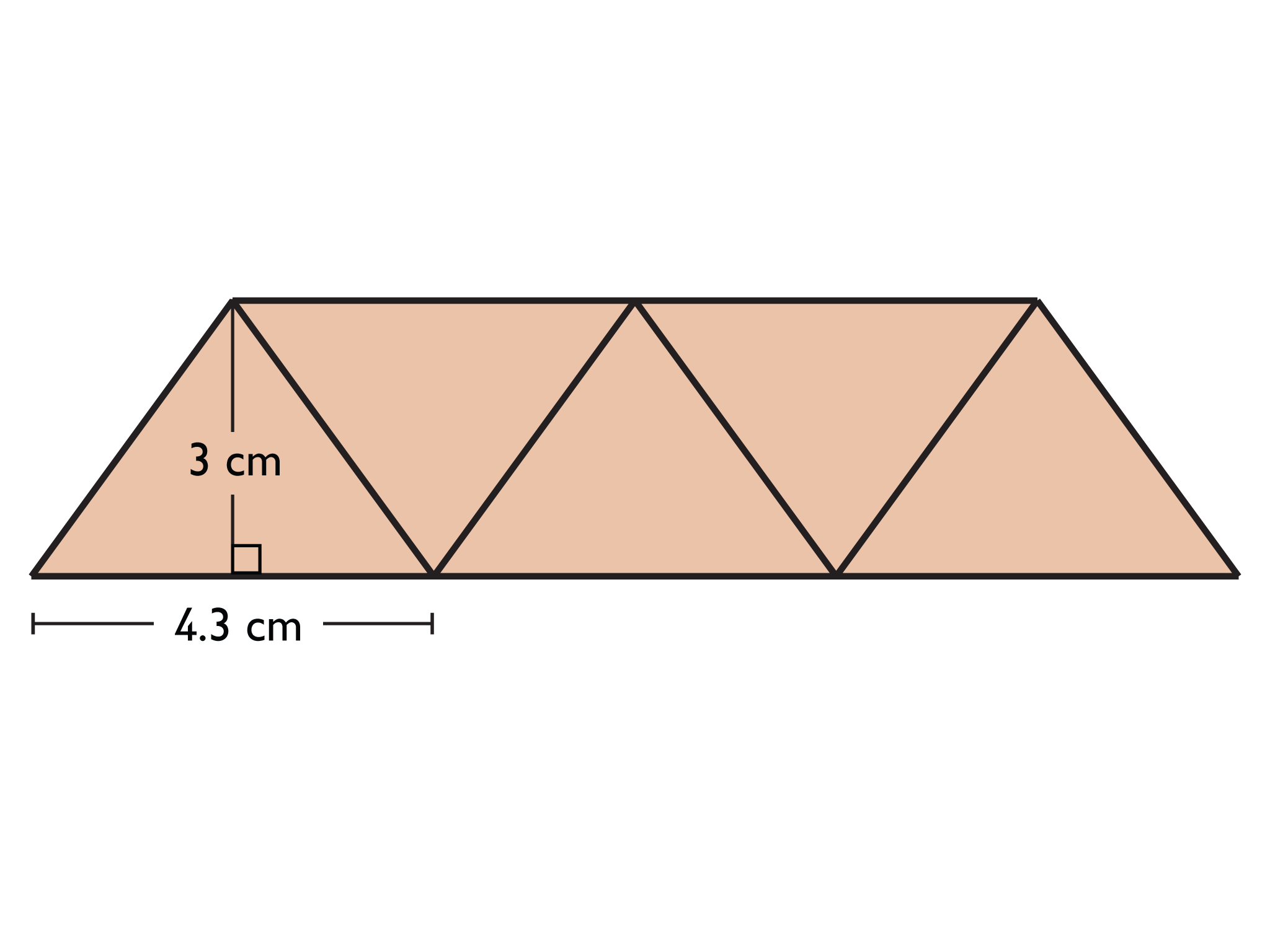
Pentagon
Area of one triangle = 12(4.3)(3) = 6.45
Area of pentagon = 6.45 ⋅ 5 = 32.25
The area of the pentagon is 32.25 square centimeters.
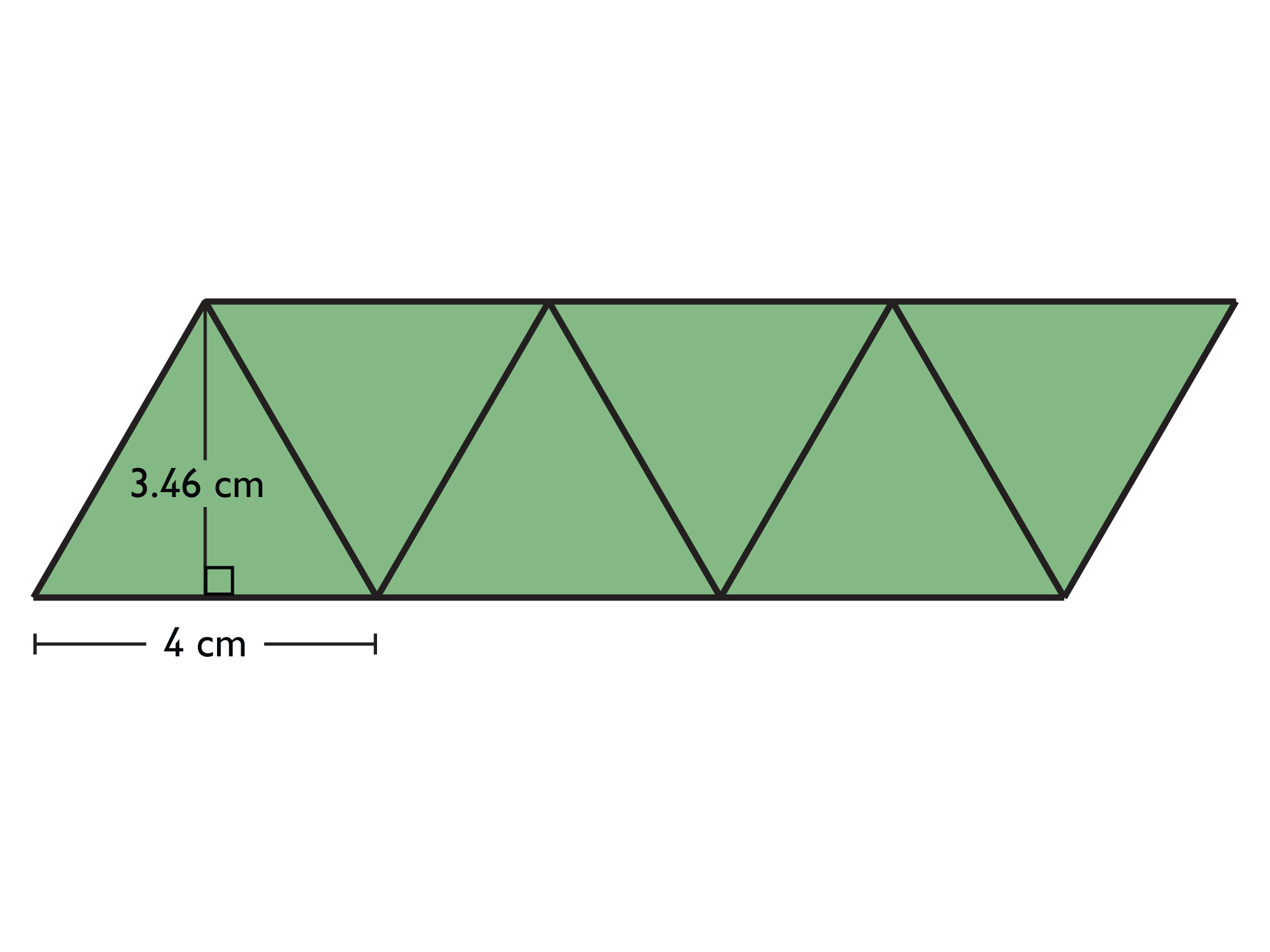
Hexagon
Area of one triangle = 12(4)(3.46) = 6.92
Area of hexagon = 6.92 ⋅ 6 = 41.52
The area of the hexagon is 41.52 square centimeters.
- Students will find the area of a second polygon, time permitting.
Work Time
Find the Area of Regular Polygons
All of these figures are regular polygons. In each figure, a vertical line has been drawn from the center of the figure to the midpoint of a side. This line is called the apothem. Note that the center of a regular polygon is the same distance from the midpoint of any side. Choose one of these figures, then:
- Use the length of the apothem and the side length to find the area of the polygon. (To get started, think about how you could divide the polygon into shapes that you know how to find the area of.)
- If you have time, find the area of a second polygon.
Hint:
- How could you divide the polygon into triangles?
- How could you divide the polygon into parallelograms?
- How could you use the triangles to make a parallelogram that represents the total area of the polygon?
Find the Area of Regular Polygons
Possible Answers
- The side length of the cabin is 20 feet. (The distance across is 40 feet, or two side lengths, because this is a regular hexagon and each triangle is equilateral.) The apothem is half the width of 34 feet 7.75 inches, or 17 feet 3.875 inches. Converting 3.875 inches to feet: 3.875 ÷ 12 ≈ .32. So, 17 feet 3.875 inches is about 17.32 feet.
Area of one triangle sq ft
Area of the cabin = 173.2 ⋅ 6 = 1,039.2 sq ft
The area of the cabin is about 1,039.2 sq ft
The area of the cabin is about 1,039.2 sq ft.
Work Time
Find the Area of Regular Polygons
Look at this floor plan of a build-it-yourself log cabin. Assume the cabin is a regular polygon.
- What is the area of the cabin?
Prepare a Presentation
Preparing for Ways of Thinking
Look for this type of response to be shared during the Ways of Thinking discussion:
Look for these different methods of finding the area of the polygons so that they can be compared during the class discussion:
- Students who see that the polygons can be divided into congruent isosceles triangles, and students who can generalize that any regular polygon can be divided into congruent triangles
- Students who find the area of each triangle (the apothem multiplied by the base, divided by two) and multiply by the number of sides
- Students who multiply the apothem by half the perimeter
- Students who find the area of a right triangle (half of the isosceles triangle) and multiply by twice the number of sides, thinking in terms of a rectangular area
- Students who notice that the length of the base is getting shorter relative to the apothem (these students may speculate about what will happen when the polygon has many sides—moving toward a circle—or realize, for example, that a regular decagon with an apothem of 6 cm and side lengths of 8 cm is not possible)
Possible Answers
- Presentations will vary.
Challenge Problem
Possible Answers
- Each side is 5 in. long.
There are 6 sides.
30 ÷ 6 = 5
Work Time
Prepare a Presentation
Prepare a presentation about finding the area of regular polygons. Support your thinking with your work.
Challenge Problem
If the area of a regular hexagon is 64.5 square inches, and the apothem is 4.3 inches, how long is each side?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- What ideas did you have for finding the area at the start of Work Time?
- How is the apothem like the radius of a circle?
- What patterns did you notice in dividing the polygons (e.g., number of triangles, length of the parallelogram)?
- When you printed the polygons, were the actual measurements the ones given in the drawings? Why?
This question has to do with scale and understanding that although the drawings most likely did not print at actual size (the computer screen scales images to fit), they still are proportional.
- The pentagon was different from the other polygons, but how was it the same?
- How would you find the area of a regular polygon with 20 sides?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
Performance Task
Ways of Thinking: Make Connections
Take notes about other students’ approaches to finding the area of regular polygons.
Hint:
As your classmates present, ask questions such as:
- How is the apothem like the radius of a circle?
- How was your approach to finding the area of the pentagon different from your approach to finding the areas of the other polygons? How was it the same?
- What did you do first when solving the cabin problem—that is, how did you make sense of the problem?
Area of Regular Polygons
A Possible Summary
- To find the area of many polygons, break them up into figures whose areas can found (such as triangles, rectangles, trapezoids, or parallelograms). In the case of regular polygons, because all of the sides are congruent, they can be broken up into the same number of congruent triangles as there are sides. Multiplying the apothem by half of the perimeter gives the area of the regular polygon.
Formative Assessment
Summary of the Math: Area of Regular Polygons
Write a summary about finding the area of regular polygons.
Hint:
Check your summary.
- Do you explain how to find the area of a regular polygon in at least two ways?
- Do you explain how a regular polygon is different from a polygon that is not regular, in a way that makes it easier to find its area?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for finding the area of regular polygons. If you notice any insightful comments about finding the area of regular polygons, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some places I see regular polygons are …