- Author:
- Chris Adcock
- Subject:
- Geometry, Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Scale

Overview
Students will explore scale and use it to find measurements in scale drawings.
Key Concepts
Scale drawings are drawn proportionally so that there is a ratio between a given length on the drawing and the actual length. This ratio is used to set up a proportion to find other measurements.
Goals
- Understand that scale drawings are proportional.
- Use scale to find actual measurements.
ELL: Define these terms in the context of the discussion:
- scale
- scale drawing
- scaled to fit
- proportional
Allow ELLs to use the dictionary if they wish.
Modeling
Lesson Guide
Show the video of the architect and discuss mathematical modeling and scale drawings.
ELL: When showing the video, be sure that ELLs are following the explanations. Pause the video as necessary to allow ELLs time to process the information. Ask students if they need to watch it a second time. Consider asking some questions to check for understanding.
Opening
Modeling
- Watch the video.
- Discuss how this architect uses mathematical modeling in his work.
VIDEO: Architect
Modeling
Lesson Guide
Show students the drawing of the One World Trade Center building and give them time to think about the height of the building and how they might estimate the height.
Mathematics
Briefly discuss how students might be able to estimate the height of the building. Explain this is a photograph that shows the One World Trade Center, although we don’t know the scale. It is important to note the difference between scale drawings, perspective drawings, or photographs. Some photographs can be taken at different perspectives and can make things appear shorter or taller than they really are. Since this picture is taken from an angle, not looking straight on, we can’t really find the actual height of the building. In addition, another reason why we can't find the height is because there are no trees or people in the drawing to compare to. Some architectural drawings include a person to give a sense of scale, but in this case, a person would be too small to help.
Discuss the idea that scale drawings are proportional to the actual object they represent. The ratio between the length and the actual length is called the scale. This ratio can be used to set up a proportion to find other measurements.
Opening
Modeling
This is a city view of One World Trade Center in New York City.
- How tall do you think the building is (including the antenna)?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find measurements using scale drawings.
Opening
Find measurements using scale drawings.
Interpreting Scale from a Picture
Lesson Guide
Have students work in groups. Give students time to work out how to use scale before prompting them. Make sure each group understands how to use scale before students move on to the remaining tasks.
Preparing for Ways of Thinking
Look for these types of responses to be shared during the class discussion:
- Students who use the scale more accurately, rather than rounding to multiples of the scale
- Students who use different methods to answer the question (multiplying versus using a proportion) so that these can be compared during the class discussion
ELL: Define the term approximations in the context of the discussion. Allow ELLs to use the dictionary if they wish.
Interventions
Student has difficulty getting started.
- If the building were as tall as eight 200-ft sections, how tall would it be?
- Can you show that relationship as a proportion?
1 length = 200 ft, 8 lengths = ____ ft?
Student does not set up the proportion correctly.
- What is one length compared to?
- How many of those lengths make up the distance you want to measure?
- Lengths are compared to distance in both ratios.
Student has a solution.
- How accurate do you think your answers are?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Look for students who work out how to use scale and can explain it.
Mathematical Practice 6: Attend to precision.
- Students should see that most of the measurements are approximations due to the size of the drawings (if 1 in. on the actual drawing represents a distance, it does not show as 1 in. on screen and can’t be measured accurately), and that it is difficult to be precise.
- Look for students who label their answers with the correct units.
Possible Answers
- One World Trade Center is a little more than eight 200-ft sections tall.
- Answers will vary. The building is 1,776 ft tall (note this measurement symbolizes the year 1776). Students would most likely multiply 200 by 8, but they should also see the proportion that leads to this calculation:
Work Time
Interpreting Scale from a Picture
Scale is difficult to determine with nothing to refer to. The One World Trade Center building has a cube-shaped base that is 200 ft in height, with trapezoid and triangle faces rising above the cube. You can use the picture of the One World Trade Center, as well as what you know about the height of its cube base, to approximate the height of the building.
- Approximately how many 200-ft sections is the building in height?
- How tall do you think the building is?
Hint:
- What do you need to measure on the drawing to find the scale of the drawing?
- To find the height of the building, think about what you need to solve for.
- How can you set up the equation?
Interpret Scale Drawings
Interventions
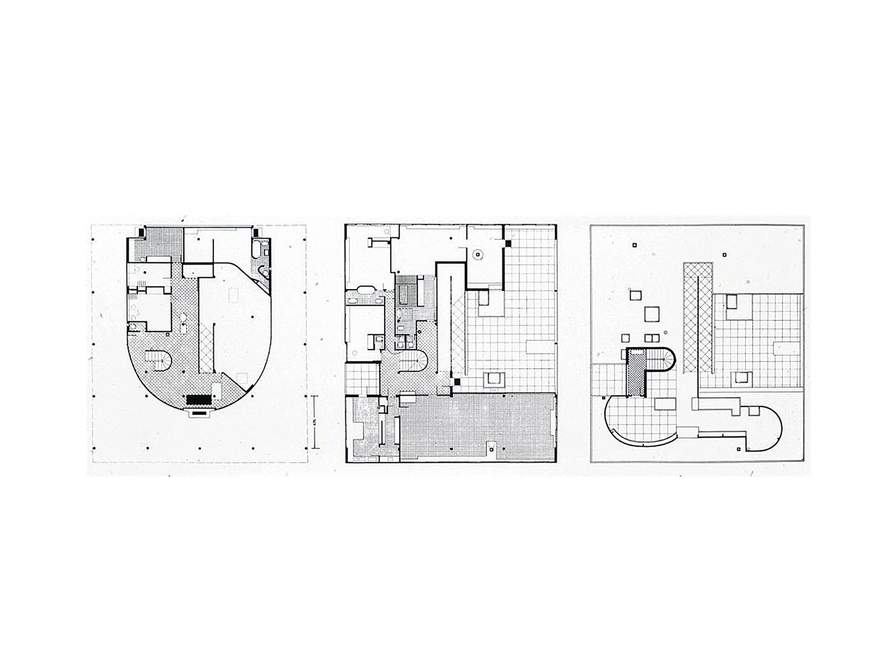
Student does not understand the proportional relationship between the drawing and the actual object.
- What shapes do the grids of columns make in the Villa Savoye? (squares)
- These shapes are shown in the drawings. Would they be true in the actual building?
Possible Answers
- The house (Villa Savoye) is 4 sections wide: 4 ⋅ 4.75 m = 19 m. The house is a little longer than 4 sections long, hanging over a little on either end, so about 4.5 sections: 4.5 ⋅ 4.75 m = 21.375 m ≈ 21 m. Again, proportions can be used:
Width:
Length:
- The living room takes up about 5 squares of the grid. Each square has an area of 22.5625 m (4.75 m ⋅ 4.75 m = 22.5625 m)
22.5625 m⋅ 5 = 112.8125 m or about 113 m
Work Time
Interpret Scale Drawings
Villa Savoye is a house designed by the Swiss architect Le Corbusier. It was built between 1928 and 1931 and is considered a prime example of modern architecture and the International Style.
Look at the photo and the floor plans of the house.
- If the columns are 4.75 m apart, what are the length and width of the house?
- What is the area of the living room (the gridded area in the middle drawing of the second floor)?

Hint:
- What is the scale expressed as a ratio?
- What are you solving for?
- How can you set up the equation?
- How can you estimate area?
Interpret Scale Drawings
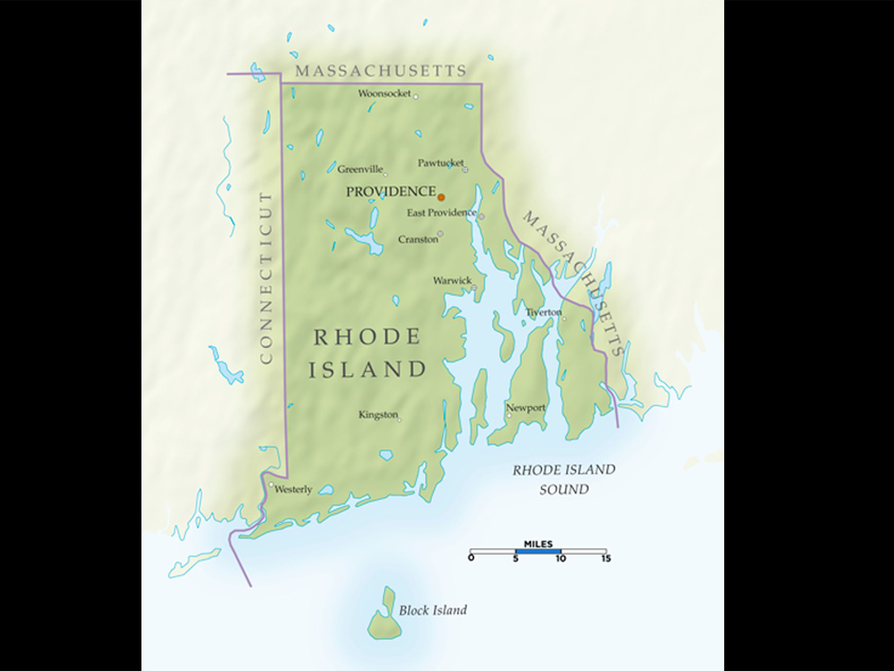
Possible Answers
- The scale is one length equals 15 mi.
- It is about 25 mi, or about 1.67 lengths, from Providence to Newport.
- The distance from the top of the state of Rhode Island to the bottom is a little more than 3 lengths, or 48 mi. (The state is actually 48 mi long.)
Work Time
Interpret Scale Drawings
This is a map of Rhode Island, the smallest state in the United States.
- What is the scale of the map?
- What is the distance between Providence (the state capital) and Newport?
- Excluding Block Island, what is the distance from the top of the state to the bottom of the state at its southernmost point?
Hint:
- What is the scale expressed as a ratio?
- How can you use the scale to determine distances?
Interpreting Scale of a Globe
Preparing for Ways of Thinking
Look for these types of responses to be shared during the class discussion:
- Students who see that the scale for the globe could be stated as 1 ft : 7,900 mi. (This response is insightful, but these students should also realize that the scale would not be useful.)
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Look for students who see the connection between the scale drawings and the scale of the computer page (for example, the 12-in. globe is about 2 in. on the screen).
Interventions
Student does not understand the proportional relationship between the drawing and the actual object.
- The globe is a sphere. Is the earth a sphere?
Possible Answers
- Students could say that the scale is 1 ft : 7,900 mi, but that wouldn’t be very useful for finding measurements. The ratio is 12 in. to 7,900 mi, but needs to be expressed as a unit ratio. Explain to students that this is typically the way scale (and many rates) is expressed.
So, the scale is about 1 in. : 658 mi.
- Africa is about 4,600 mi wide. Students should see that Africa at its widest point is about half of the diameter of the globe (actually a little more than half).
Work Time
Interpreting Scale of a Globe
This globe has a diameter of 12 in.
- If the earth has a diameter of about 7,900 mi at the equator, what is the scale of the globe?
- About how wide is Africa in miles at its widest point?
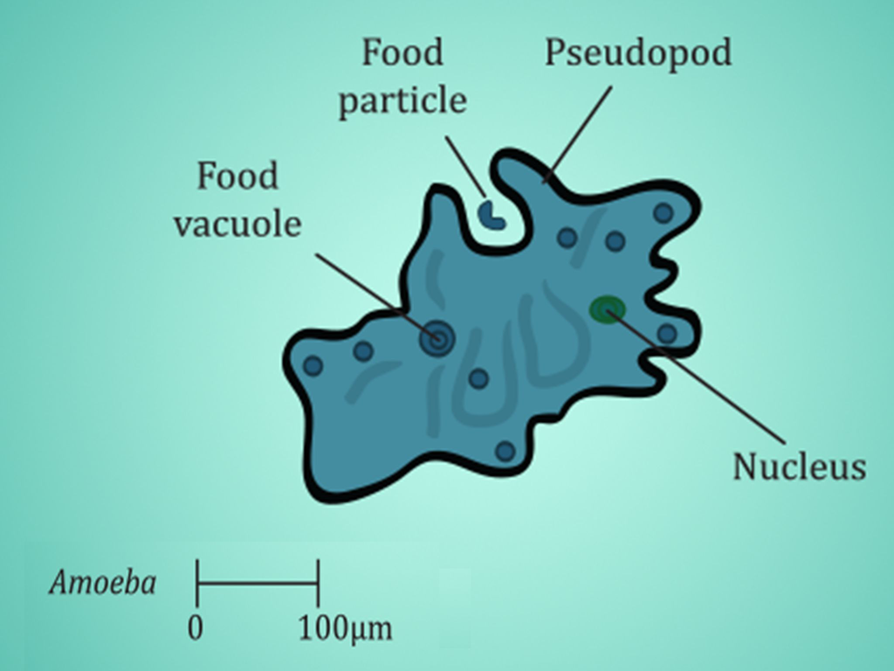
Interpret Scale Drawings
Preparing for Ways of Thinking
Look for these types of responses to be shared during the class discussion:
- Students who see that 100 micrometers are 110 of a millimeter, and that the amoeba would be barely visible to the naked eye, as it would be nearly half (0.4) a millimeter wide.
Possible Answers
- Since a micrometer is 0.000001 of a meter, 100 μm is 0.0001, or of a meter. A millimeter is of a meter, so 100 μm is of a millimeter. The amoeba is about 4 lengths of the scale, or 0.4 mm long. This size would make the amoeba barely visible to the naked eye.
- The nucleus is about of the length of the scale or about 30 μm, so it is 0.03 mm long. This problem illustrates the reason why scale is used: Clearly a building can’t be drawn actual size, and neither can something very small, such as an amoeba.
Challenge Problem
Answers
The model would be about 54 in. tall, or 4 ft.
This problem shows how using a proportion helps to understand the relationship between the scaled object or drawing and the real thing. The only difference in this problem is that a different unit of measure is being solved for:
Work Time
Interpret Scale Drawings
In this drawing of an amoeba, the scale is in µm, which stands for micrometer; 1 micrometer is of a meter.
- What is the approximate length of the amoeba in micrometers?
- About how long is the nucleus in micrometers?
Challenge Problem
The Burj Khalifa in Dubai is currently the tallest building in the world at 2,717 feet—which is a little more than half of a mile.
- If a model of the building were made at a scale of 50 : 1—that is, 50 ft to 1 in.—how tall would the model be?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How accurate do you think your results were? Why?
- Why is scale used?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- How could you measure more accurately?
ELL: Consider presenting some of the questions in writing to support ELLs. Also, consider providing sentence frames, such as the following (in the order the questions were given):
“In terms of accuracy, I think my results were…”
“I say that because…”
Performance Task
Ways of Thinking: Make Connections
Take notes about other students’ approaches to using scale drawings to find measurements.
Hint:
As your classmates present, ask questions such as:
- How accurate do you think your results are? Explain.
- How is the image on your screen different from the actual drawing or model?
- Why is scale used?
- How did you make sense of the problem? What did you do first?
- How could you measure more accurately?
Scale Drawings
A Possible Summary
Scale drawings and models are used to show things that are too big or too small to be seen easily at their actual size. Scale drawings are proportional. There is a ratio between a given length and the actual length called the scale. This ratio is used to set up a proportion to find other measurements. A computer screen shows a scale version of the scale drawing or model to fit the screen. Consequently, the measurements are approximations, but they still give a good idea of the proportions of the object.
Formative Assessment
Summary of the Math: Scale Drawings
Write a summary about scale drawings.
Hint:
Check your summary:
- Do you explain why scale drawings are used?
- Do you provide an example of scale and explain what it means?
- Do you explain how to use the scale in a scale drawing to find measurements of the thing that the drawing represents?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for finding measurements by using scale drawings. If you notice insightful comments about how students find measurements by using scale drawings, plan to share them with the class tomorrow.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some places that I have seen scale used are …