Self Check Exercise

Overview
Students critique their work from the Self Check and redo the task after receiving feedback. Students then take a quiz to review the goals of the unit.
Key Concepts
Students understand how to find the area of figures such as rectangles and triangles. They have applied that knowledge to finding the area of composite figures and regular polygons. The area of regular polygons was extended to understand the area of a circle. Students also applied ratio and proportion to interpret scale drawings and redraw them at a different scale.
Goals
- Critique and revise student work.
- Apply skills learned in the unit.
- Understand two-dimensional measurements:
- Area of composite figures, including regular polygons.
- Area and circumference of circles.
- Interpret scale drawings and redraw them at a different scale.
SWD: Make sure all students have the prerequisite skills for the activities in this lesson.
Students should understand these domain-specific terms:
- composite figures
- regular polygons
- area
- circumference
- scale drawings
- two dimensional
It may be helpful to preteach these terms to students with disabilities.
ELL: As academic vocabulary is reviewed, be sure to repeat it and allow students to repeat after you as needed. Consider writing the words as they are being reviewed. Allow enough time for ELLs to check their dictionaries if they wish.
Critique
Lesson Guide
Students should look at the results of their Self Check and think about the critique questions.
Opening
Critique
Review your work on the Self Check problem and think about these questions:
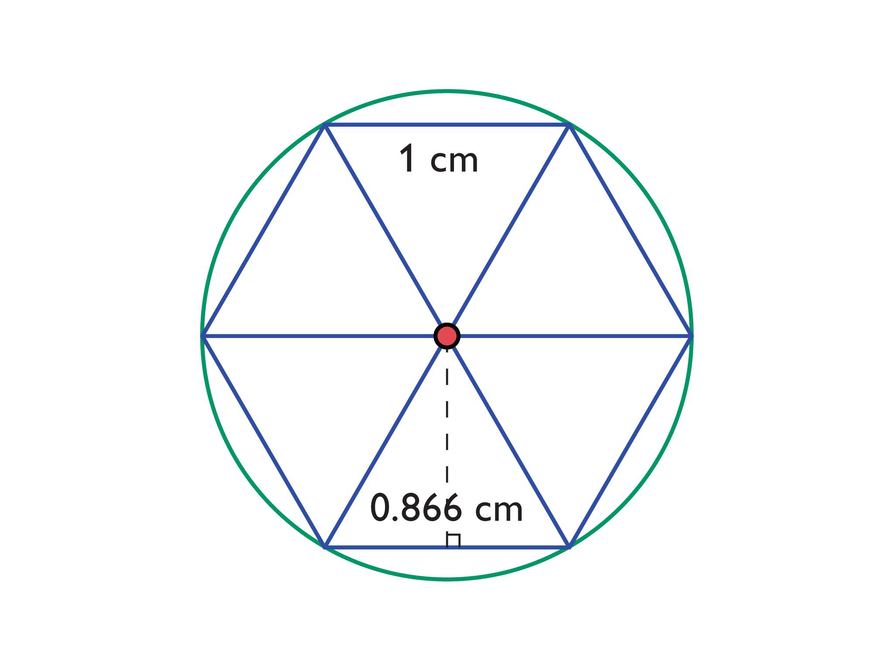
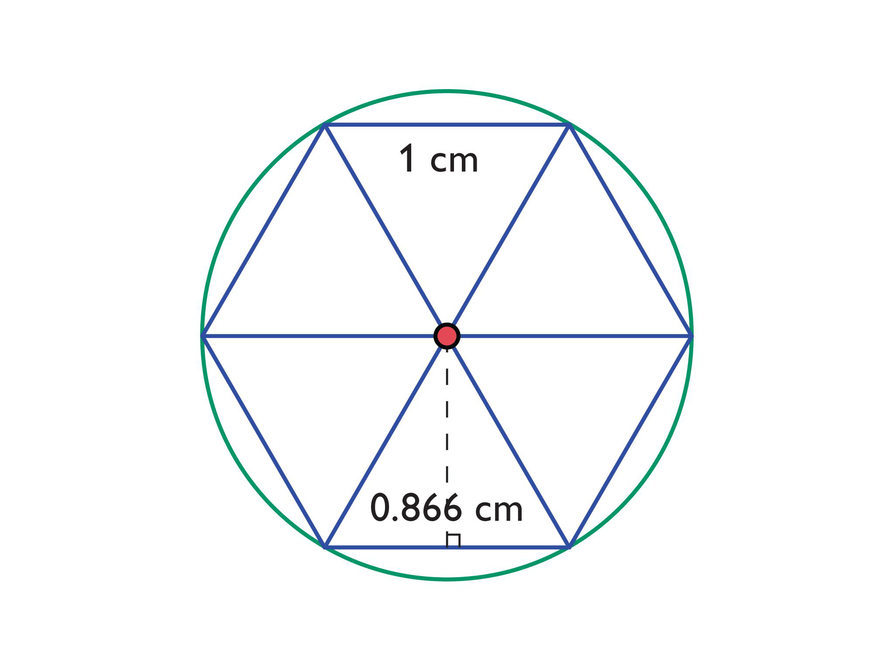
- What type of triangles is the hexagon divided into?
- What is the base length and height of each triangle?
- How do you find the area of a triangle?
- What is the radius of the circle?
- What is the length of the apothem and hexagon side?
- If 1 cm becomes 2 ft in the new drawing, what factor does 1 cm increase by?
Now, find a different way to solve the problem.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will apply what they know about two-dimensional measurement to solve a multistep area and perimeter/circumference problem.
SWD: Students with disabilities may have difficulty applying the skills that they have learned in this unit to a new task. It may be helpful to model for students how to apply measurement skills to new shapes.
Opening
Solve a multistep area and perimeter/circumference problem.
Revise Your Work
Lesson Guide
Have students work with their partners. Give out a fresh piece of paper to each pair of students. Ask them to try the task again, this time combining their ideas.
As students work with their partners, you have two tasks:
- Note different student approaches to the task.
- Note students’ chosen problem-solving approaches.
Attend to these questions:
- Which math do students choose to use?
- Which resources do students ask for?
Attend in particular to the students’ mathematical decisions:
- Do students track their progress in using their chosen mathematics?
- Do students notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
- Do students use the formulas for area and circumference of a circle correctly?
- Do students apply scale to find actual dimensions?
Try not to make suggestions that move students toward a particular approach to this task.
SWD: Students with disabilities may struggle to self-monitor the effectiveness of strategies. Consider helping students to reflect by modeling think-aloud strategies if students are demonstrating difficulty shifting gears from an ineffective strategy.
ELL: When eliciting answers, be aware of the difficulties some ELLs encounter when they have to express themselves in a foreign language. For example, if you hear them say the right things but use the wrong grammatical structure, show signs of agreement and softly rephrase with the correct grammar using the student’s words as much as possible.
Interventions
Student has difficulty getting started.
- What do you already know? What do you need to know?
- How long is the circumference in the drawing? How long is it in real life?
- How can the figure be broken down into figures that you know the area of?
Look for students who use different methods to break down figures into figures they know the area of, and compare their methods during the class discussion.
Answers
The hexagon has area 2.6 cm:
= 0.866()
= 0.866 ⋅ 3
= 2.598
The circle has area 3.14 cm:
= (3.14)(1 ⋅ 1)
= 3.14
The circle area is larger than the hexagon area. The difference is: 3.14 cm− 2.6 cm = 0.54 cm.
The perimeter of the hexagon is 6 cm because each side is 1 cm. The circumference of the circle is 6.28 cm:
C = πd C = 3.14(2) C = 6.28
The circumference is longer than the perimeter of the regular hexagon by 0.28 cm (6.28 cm − 6 cm = 0.28 cm).The dimensions will be doubled (with different units) because 2 ft are replacing 1 cm. The side lengths and radius will be 2 ft, and the apothem will be 0.866 in. ⋅ 2 ft/in = 1.732 ft. The hexagon will have area 10.39 ft:
= 1.732 ⋅ 6 = 10.392
The circle will have area 12.56 ft:
= (3.14)(2 ⋅ 2) = 12.56
Work Time
Revise Your Work
Work with a partner and try the task again, this time combining your ideas.
Self Check:
- What is the area of the regular hexagon? What is the area of the circle? Compare the two areas.
- What is the perimeter of the regular hexagon? What is the circumference of the circle? Compare the two lengths.
- If the figure were redrawn at a scale of 1 cm : 2 ft, what would the area of the regular hexagon in the drawing be? What would the area of the circle be?
Make Connections
Mathematics
Organize a whole class discussion to consider issues arising from the work students did to revise their work. You may not have time to address all these issues, so focus your class’s discussion on the issues most important for students.
Have students share their work and talk about how they approached the problem. Students with strategies that didn’t work should share so they can talk about how and when they realized their strategy didn’t work and what they did about it. Have students share the Self Check assessment questions (from their teacher or generated by the system) that they addressed and how they addressed those questions. Have students ask questions and make observations as they view each other’s work.
Ask these questions:
- What part of the task was most difficult?
- Did you and your partner ever disagree about measurements? Did you resolve your difference of opinion? How?
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ approaches to revising their work and solving the problem.
Hint:
As your classmates present, ask questions such as:
- How did breaking the hexagon into triangles help you find the area of the hexagon? How did it help you find the area of the circle?
- Did you find a way to solve the problem that was different from your first approach? Can you describe both approaches?
- What errors in your work did you find that required revising? How did you go about revising the mistakes?
- What part of the task was most difficult?
- Did you and your partner ever disagree about some aspect of the problem? Did you resolve your difference of opinion? How?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see how students apply what they know about two-dimensional measurement to solve a multistep area and perimeter/circumference problem. If you notice insightful comments, plan to share them with the class in the next lesson.
ELL: Be sure that ELLs have access to a dictionary and some time to discuss with a partner before writing, to help them organize their thoughts. Allow ELLs who share the same primary language to discuss in their preferred language if they wish to do so.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some things I have learned about scale are …