- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Area of a Circle

Overview
Lesson Overview
Students will compare the formula for the area of a regular polygon to discover the formula for the area of a circle.
Key Concepts
The area of a regular polygon can be found by multiplying the apothem by half of the perimeter. If a circle is thought of as a regular polygon with many sides, the formula can be applied.
For a circle, the apothem is the radius, and p is C.
Goals
- Derive the formula for the area of a circle.
- Apply the formula to find the area of circles.
SWD: Consider the prerequisite skills for this lesson: understanding and applying the formula for the area of a regular polygon. Students with disabilities may need direct instruction and guided practice with this skill.
Students should understand these domain-specific terms:
- apothem
- parallelogram
- derivation
- height
- approximate (estimate)
- scatter plot
- pi
- perimeter
- circumference
It may be helpful to preteach these terms to students with disabilities.
Many-Sided Regular Polygons
Lesson Guide
Show students the nested polygons and discuss what shape the polygons are approaching.
SWD: Students with visual spatial difficulties may have trouble differentiating between the shapes that are nested in the opening graphic. If possible, provide discreet images of each shape so that students can see how the shapes evolve into a circle.
Mathematics
Discuss the opening questions briefly, taking only a few comments and observations—students will answer the questions as they do the activity.
Students will see that the polygons are approaching the shape of a circle. They know how to find the area of a regular polygon, so they could use a many-sided regular polygon to approximate the area of a circle.
Emphasize that the more sides a regular polygon has, the closer it is to being a circle.
Opening
Many-Sided Regular Polygons
- Experiment with the shape of this polygon by adding more sides. As you increase the number of sides, what shape does the polygon get close to?
- Observe what shape the polygon gets close to as its sides increase in number. How do you think your observation would help you figure out a way to find the area of that shape? Explain.
INTERACTIVE: Circle 2
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use what they know about the area of a regular polygon to determine the formula for the area of a circle.
Opening
Use the areas of regular polygons to determine the formula for the area of a circle.
The Formula for the Area of a Circle
Lesson Guide
Have students work in groups. Give students time to struggle with the problem before prompting them. Make sure each group has arrived at the formula before they move on to the remaining tasks.
ELL: As mentioned in other lessons, if you hear ELLs say the right things but use the wrong grammatical structure, show signs of agreement and softly rephrase using the correct grammar and the student’s words as much as possible. If a student says, “The triangles are similar in the two figures, they all have the same size,” you could agree and say, “Yes, they both have 16 congruent sections that are very close in size.”
Interventions
Student has difficulty getting started.
- What is the perimeter of a circle called?
- How do you find its length?
- What line in a circle is the same as the apothem?
Student has a solution.
- If you could measure pi more accurately, how much difference do you think that would make in the answer?
Student does not think that the area of a circle can be found accurately because there are no straight sides.
- Would a 1,000-gon with an apothem of 6 ft have the same area as a circle with a radius of 6 ft?
- How much difference would there be in the areas?
- What number should you use for π?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Look for students who work out the area formula and can explain it.
Mathematical Practice 6: Attend to precision.
- Look for students who label their answers with the correct square units.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Students should see the similarities between regular polygons and circles.
- Look for students who see that the area of the circle is the same as a regular polygon with a number of sides approaching infinity, and who remember that the interior angle of the polygon is approaching 180°.
Possible Answers
- They both have 16 congruent sections that are very close in size (comparing the wedges to the triangles). Students may also notice the similarities in the parallelogram dimensions.
- The length along the edge of the parallelogram-like shape is half of the circumference and the height is the radius.
- To express area in terms of the radius r :
Replace C with πd.
Replace d with 2r.
Divide by 2.
Work Time
The Formula for the Area of a Circle
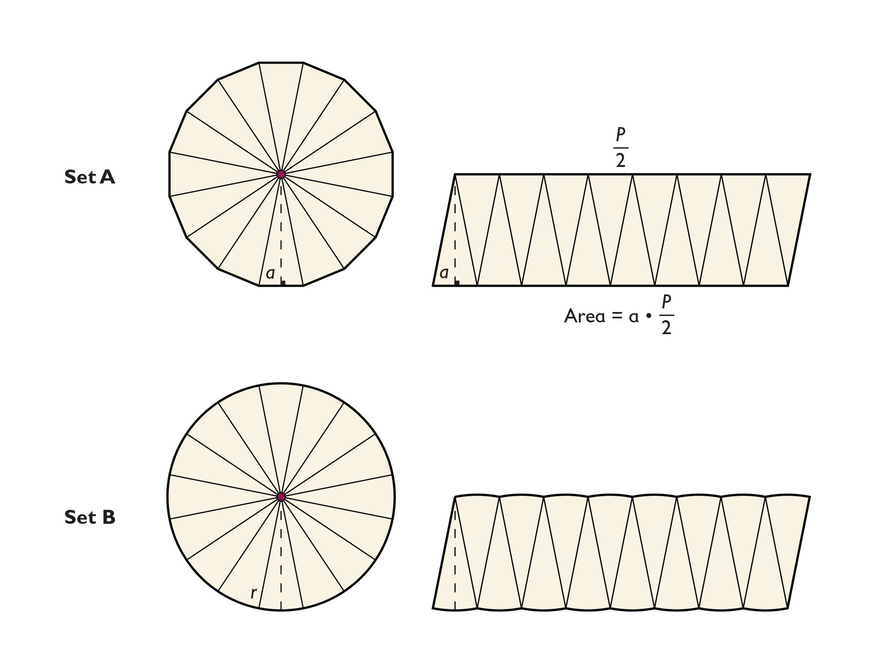
Set A contains a 16-gon divided into 16 congruent triangles and the same 16-gon rearranged into a parallelogram made up of the 16 congruent triangles. The perimeter of the polygon is labeled p and the apothem is labeled a.
Set B contains a circle divided into 16 congruent sections and the same circle rearranged into a parallelogram-like shape, which is made up of the 16 congruent sections. The radius is labeled r.
- Look carefully at the two sets of figures. How are they similar?
- What is the length of the parallelogram-like shape formed from the circle? What is the height?
- How could you express the area of the circle in terms of r?
Hint:
- What is the “apothem” of a circle called?
- What is the perimeter of a circle called?
The Formula for the Area of a Circle
Interventions
Student has difficulty with Task 4.
- What is the area of each small square? What are the length and width of the small square?
- What is of 4 squares?
Student does not apply the formula correctly.
- Did you use the radius or the diameter?
- Did you remember to square that length?
- What number did you use for π?
Possible Answers
- The area is . Each small square has an area of .
- Pi (π) is a little more than 3, so this is a pretty good approximation of the formula.
- Presentations will vary.
Work Time
The Formula for the Area of a Circle
In the last problem, you used the formula for the area of a polygon to come up with the formula for the area of a circle. The steps that follow will “lead you” to the formula for the area of a circle in a different way.
- What is the area of the large square?
- If each quarter of the circle takes up about three-fourths of each small square, what is the approximate area of the circle?
- How does your answer compare to the formula you wrote for the area of a circle in the previous problem?
Hint:
- To find the area of the large square, find the area of each small square.
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to be shared during the class discussion:
- Students who see the relationship between the polygon and the circle and understand that as more sides are added to the polygon, its area is approaching a circle with the same apothem/radius
- Students who apply the area formula correctly
- Students who see that units need to be square units for area and make the connection with the circle within the square
- Students who can clearly explain the relationship between the circle’s area and the square’s area
Possible Answers
Presentations will vary.
Challenge Problem
Answer
The radius is 20 ft. If the area of a circle is about 1,256 ft2, the radius can be solved for:
Using A ≈ 1,256 and π ≈ 3.14:
400 =
r = 20
Work Time
Prepare a Presentation
Prepare a presentation about the area of a circle. Use examples of your work to illustrate your explanation.
Challenge Problem
If the area of a circle is approximately 1,256 square feet, what is the radius? (Use 3.14 for π .)
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How did you discover the formula for the area of a circle?
- How was the formula similar to the formula for the area of a regular polygon?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- Why were the measurements in square units?
- If you found the area of the circles from the objects you measured in class, how accurate do you think those measurements would be? How much would the precision of pi help?
ELL: As with other discussions, consider presenting some of the questions in writing to support ELLs. Also consider providing sentence frames, such as the following (in the order the questions were given):
If possible, provide sentence frames following this format for the remainder of the questions.
- “The way I discovered the formula of the area of the circle is by…” or “I first did…and then I…”
- “The formula was similar to the formula for the area of a regular polygon in that…”
Performance Task
Ways of Thinking: Make Connections
Take notes about other students’ understandings of the area of a circle.
Hint:
As your classmates present, ask questions such as:
- How is the formula for the area of a circle similar to the formula for the area of a regular polygon?
- How did knowing the formula for the area of a polygon help you come up with the formula for the area of a circle?
- Why do you use square units for area?
Find the Area
Answers
- For a circle with a diameter of 10 in.:
d = 2r
= r r = 5
A = 3.14(5 ⋅ 5)
A = 3.14(25) = 78.5
The area is 78.5 in.2.
- For a circle with a radius of 15 cm:
r = 15
A = 3.14(15 ⋅ 15)
A = 3.14(225) = 706.5
The area is 706.5 cm2.
Remind students that units that are multiplied together are square units. Just as 10⋅10 = 102 is a “square” number, centimeters ⋅ centimeters = centimeters2 is a “square” unit.
Work Time
Find the Area
The area of a circle is equal to π times the radius squared. Approximating π with 3.14 we get the formula:
Find the areas of the following circles:
- A circle with a diameter of 10 in.
- A circle with a radius of 15 cm
Find the Area
Answers
- The area of the circular floor is 17,427.785 sq ft.
d = 2r
149 ft = 2r
= 2r r = 74.5 ft
A = 3.14(74.5 ⋅ 74.5)
A = 3.14(5,550.25) = 17,427.785
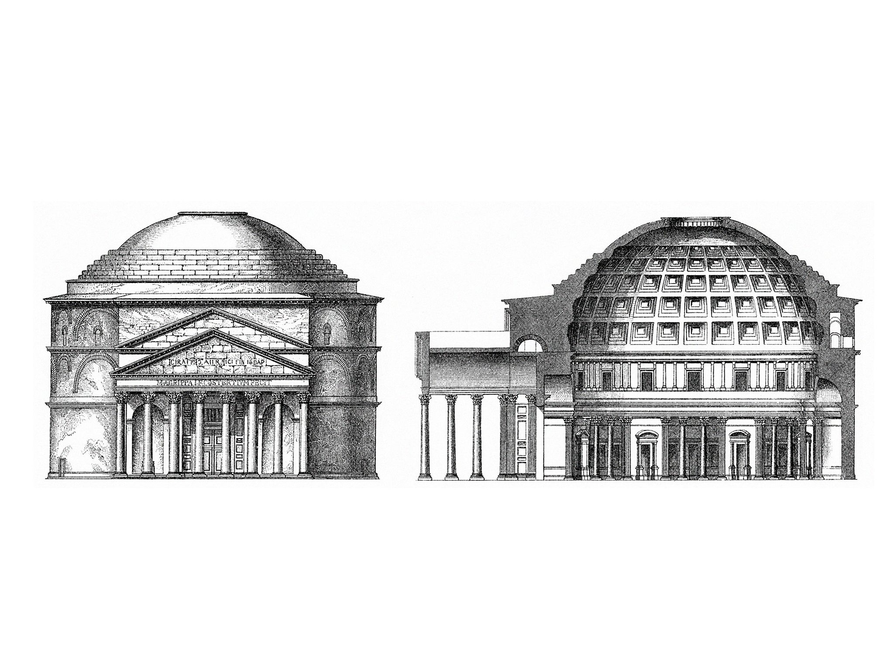
Discuss the importance of accuracy: How close does the answer need to be? How much do the significant digits affect the result? 3.1(75 ⋅ 75) = 17,437.5 or 17,437.5 sq ft, a difference of nearly 10 sq ft. The answer is an approximation regardless of how “accurate” the calculation is. (Is the Pantheon’s diameter exactly 149 ft?) We could say that the area is about 17,500 sq ft.
Work Time
Find the Area
Remember the Pantheon from the first lesson of this unit? The width of the domed part of the Pantheon is 149 feet.
- What is the area of the circular floor (which covers most of the interior of the building)?
Area of a Circle
A Possible Summary
A circle can be thought of as a regular polygon with many, many, very narrow sides. If this polygon is divided into congruent triangles and arranged into a parallelogram, its area will be very close to the circle’s area. Because of this similarity, the formula
for area of regular polygons can be changed to
for circles.
SWD: Some students may struggle with the task of actually writing a summary of the mathematics from the lesson. Possible supports:
- Prior to writing the summary, encourage students to discuss their ideas with a partner or adult and to rehearse what they might write.
- Allow students to map out their ideas in outline form or in a concept web.
Formative Assessment
Summary of the Math: Area of a Circle
Write a summary about the area of a circle.
Hint:
Check your summary.
- Do you explain how the formula for the area of a regular polygon is similar to the formula for the area of a circle?
- Do you provide the formula for the area of a circle?
- Do you explain what units are used for the area of a circle?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for determining the formula for the area of a circle. If you notice insightful comments about determining the formula for the area of a circle, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something else I would like to know about circles is …