- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Cube Building
Mathematical Practice 6
Methods Of Calculating The Surface Area

Overview
Students will continue to explore surface area, looking at more complex solids made up of cubes. Students will look at the 2-D views of these solids to see all of the surfaces and to find a shorter method to calculate the surface area.
Key Concepts
The 2-D views of 3-D figures (front top and side) show all of the surfaces of the figure (the area of the three views is doubled or the back, bottom, and other side) and so can be used to calculate surface area. The only exception is when surfaces are hidden or blocked and must be accounted for.
Goals
- Explore the relationship between 2-D views of figures and their surface area.
- Find the surface area of different solids.
Be Precise
Mathematical Practices in Action
Mathematical Practice 6: Attend to precision.
Have students watch the video introducing Mathematical Practice 6: Attend to precision. Ask students to look and listen for how their description of surface area becomes more precise as the students talked about it.
After students watch the video, give partners time to talk about how Sophie and Karen were being precise as they talked about surface area and other mathematical terms as well as their use of units. How could they improve the way that Sophie and Karen defined the terms?
Then lead a whole class discussion. Elicit student’s perceptions about how Sophie and Karen extended the meaning of area to surface area and distinguished it from volume and mass. Why is it important to be clear about whether the surface area units are inches or square inches? How can surface area increase when you remove blocks from the rectangular prism?
Point out that because opposite faces of a rectangular prism are congruent (front and back, top and bottom, left and right), students can add the three areas and multiply by 2 to find the surface area.
Opening
Be Precise
Watch the video of Sophie and Karen being precise as they find the surface area of a rectangular prism.
Discuss the following with your classmates.
- How did they become more precise in their language as they discuss the problem?
- How did they precisely specify the units in the problem?
- Can you give a more precise definition for any of the math terms Sophie and Karen use?
VIDEO: Mathematical Practice 6
Describe 3-D Figures
Lesson Guide
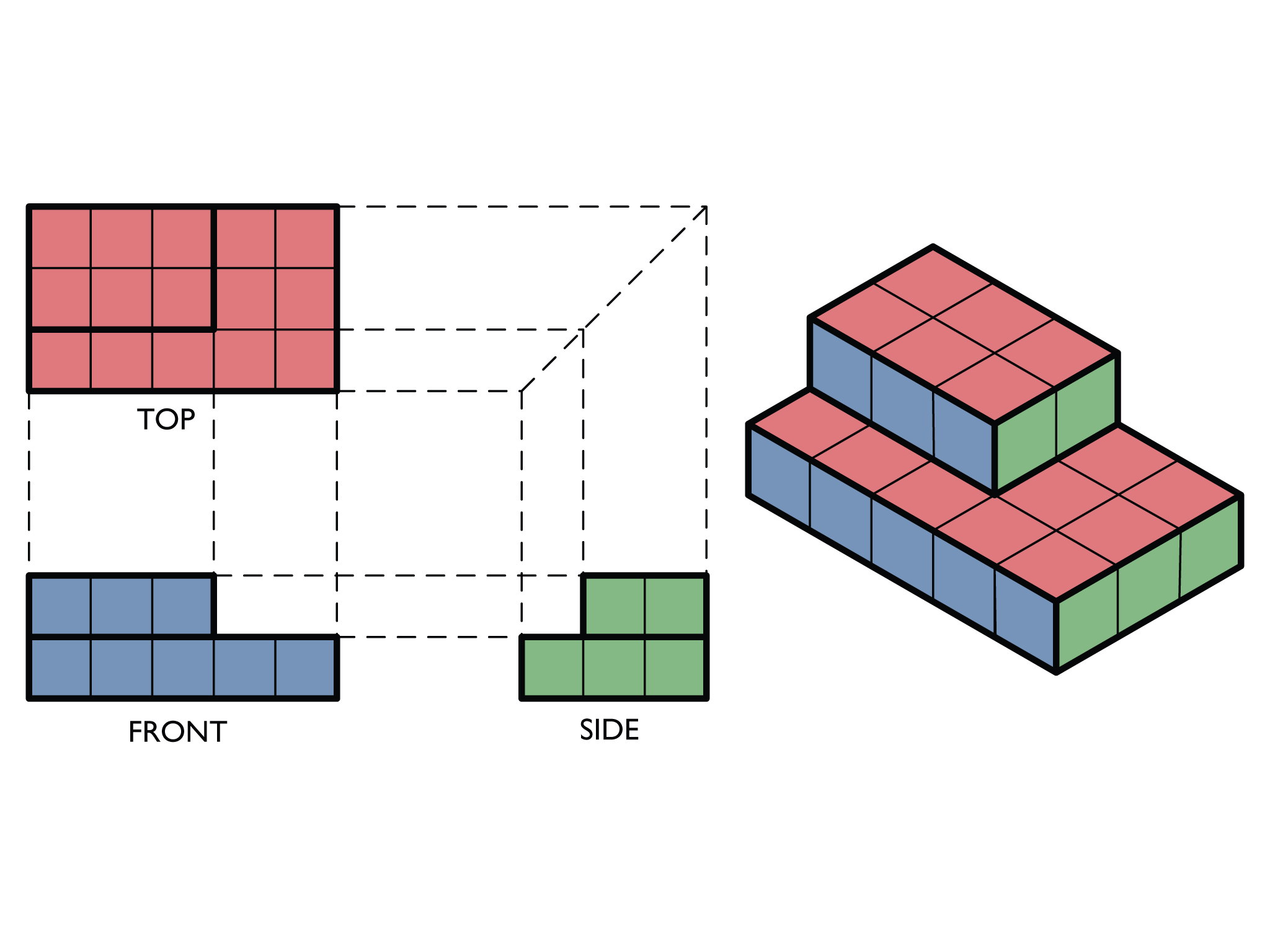
Show students the following image:
Show students how the top, front, and side views can be obtained by looking at the 3-D representation.
SWD: For students with visual-spatial vulnerabilities, it may be helpful to provide physical manipulatives to compare to 2-D representations.
ELL: This explanation offers students a rich opportunity to learn academic vocabulary. Consider displaying the new terms in writing somewhere visible in the classroom so that you have them ready for reference. Further, consider allowing ELLs to use their bilingual dictionaries to help with understanding the concepts. When possible, allow ELLs to discuss the academic vocabulary in their primary language with other ELLs who share that same primary language.
Opening
Describe 3-D Figures
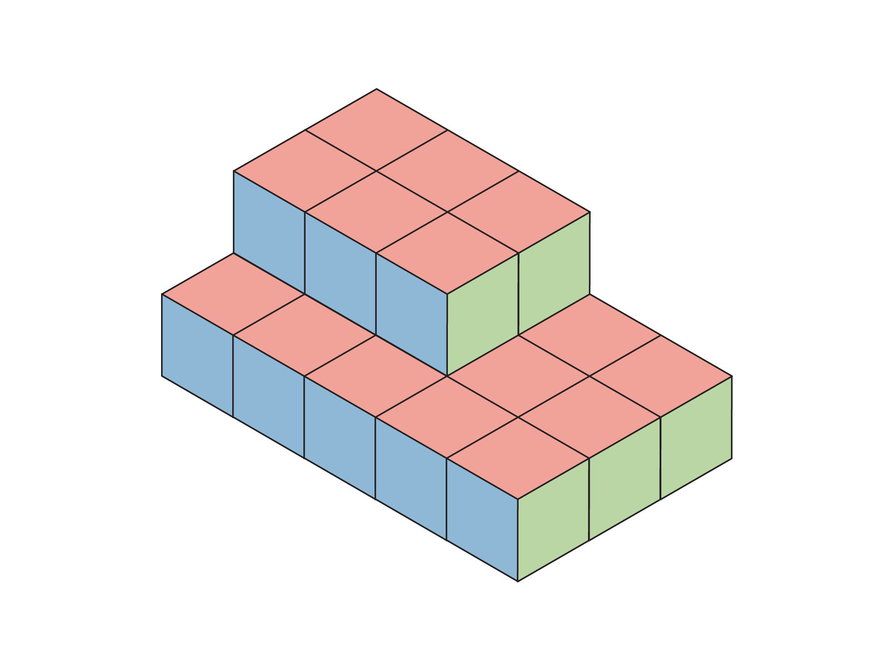
Part of attending to precision in geometry is having all the visual information necessary to understand what a 3-D figure looks like. In this lesson, you will use a method that enables you to accurately and clearly show what a 3-D figure looks like.
- What do you think this figure would look like from each side?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find the surface areas of 3-D figures.
Opening
Find the surface areas of 3-D figures.
3-D Figures
Lesson Guide
Have students work in pairs and look at the image to help them answer the questions.
SWD: Students who struggle with visual-spatial tasks may require direct instruction/explanation of how color is used to code the different views of the shape. If possible, have the 3-D shapes on hand as an added support for students who are struggling. Some students may need additional hands-on practice with 3-D shapes before making the leap to 2-D representations. Consider which shapes may be better for struggling students to start with. Providing incrementally more challenging figures may help students to better understand the concept. It may be more beneficial for a student to conceptually understand the three views of one simple figure than to go through the process of repeating the steps with other figures.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who understand how the 2-D views are related to surface area.
Mathematical Practice 5: Use appropriate tools strategically.
Look for students who see the relationship between the opposite views and realize that the views are showing surfaces and dimensions, not depth.
Some students will want to draw the 2-D views for all of the figures, while others will only need the 3-D view.
Mathematical Practice 6: Attend to precision.
Look for students who label their answers with the correct square units for the surface area.
Interventions
Student has trouble seeing the relationship between the 2-D views and the surface area.
- What makes up the surface area of the figure?
- How can you see all of the surfaces?
- Look at the front view. How many squares are facing forward?
- Look at the back view. How does it compare to the front view?
Student has a solution.
- Starting with the opening prism, how many cubes could be removed and still have the same surface area?
- How is the surface area affected if there is a hole in the figure? (In other words, some surfaces are hidden.)
Student does not think that the surface area can be found using the 2-D views.
- Pick any square on the figure. Do you see it somewhere in one of the 2-D views? Is it shown more than once?
- How many sides does a rectangular prism have? Are the opposite views the same?
- How many sides do the 2-D views show?
Possible Answers
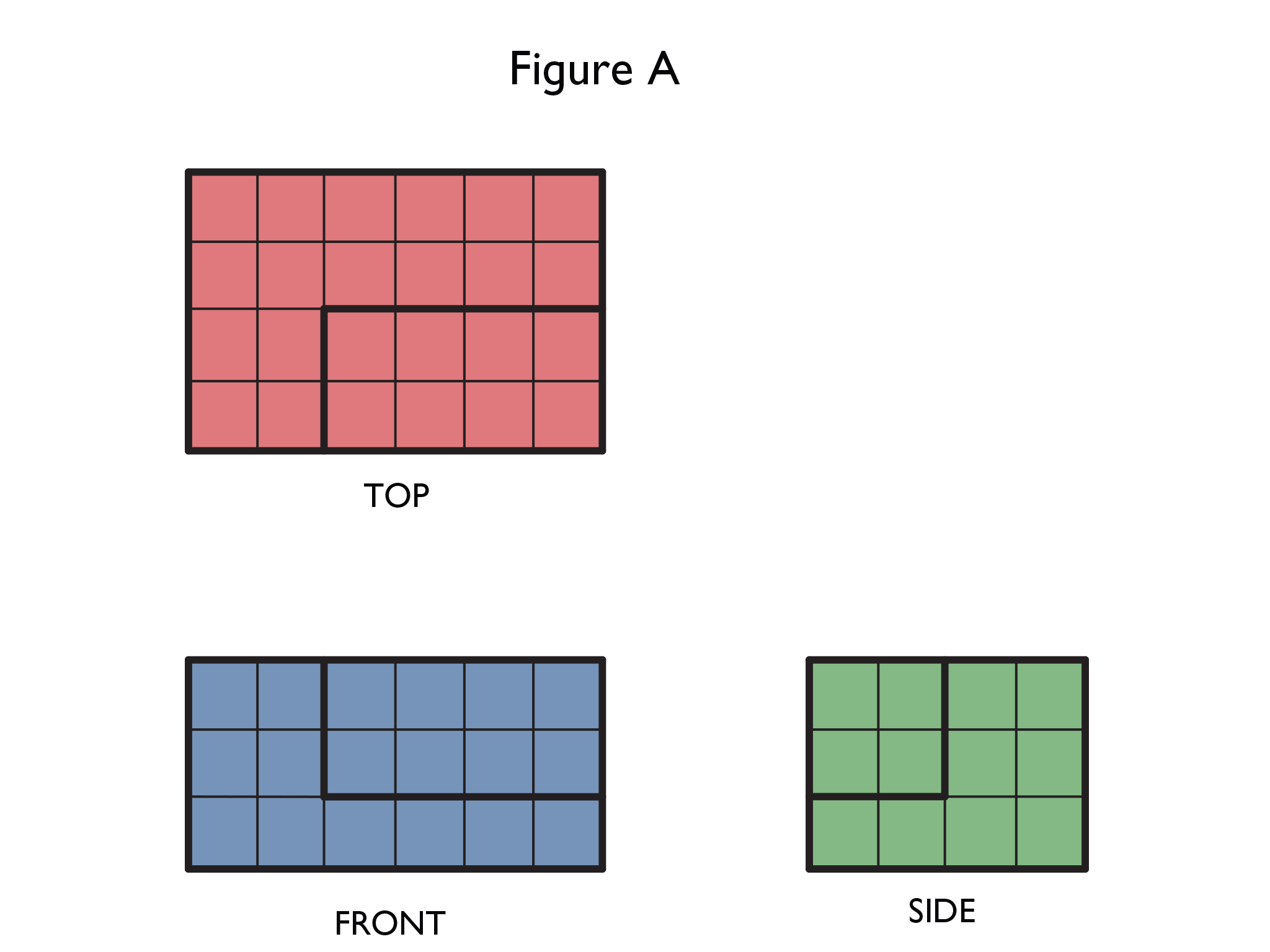
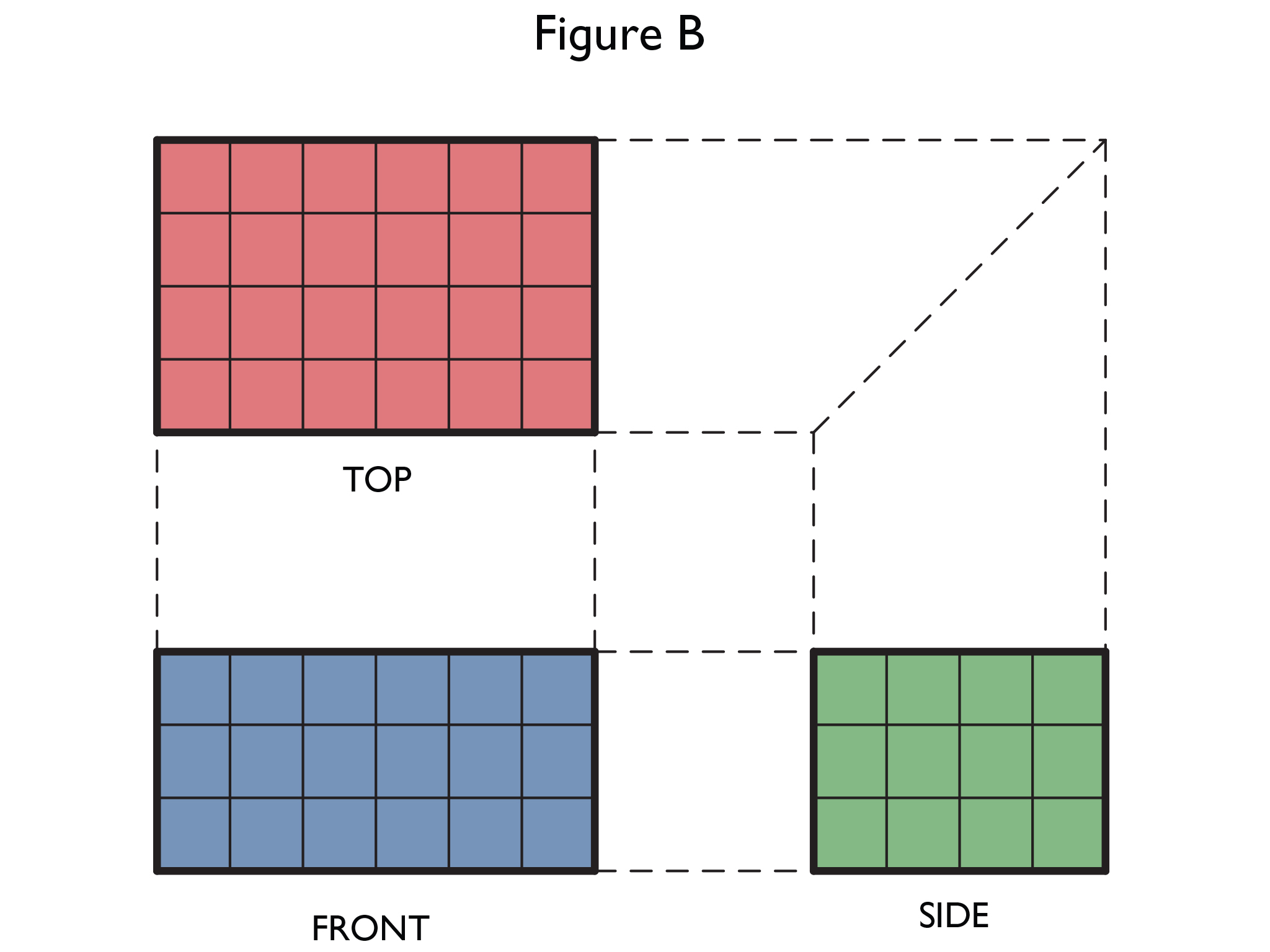
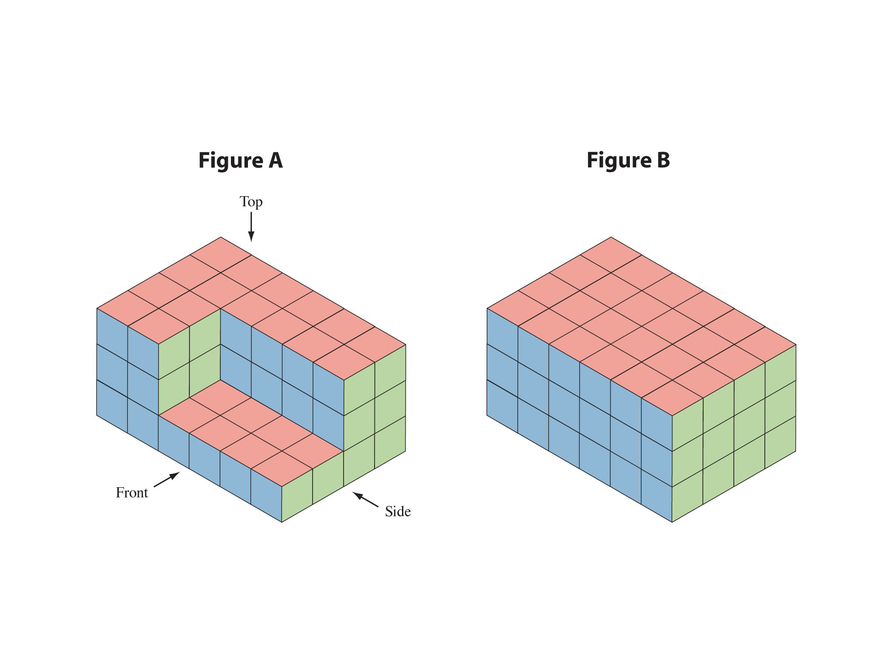
- The three views are all rectangles.
- The three views are all rectangles that are the exact same size as the rectangles in Figure A.
The surface area of each figure is the area of the three views doubled:
2[(6 ⋅ 4) + (6 ⋅ 3) + (4 ⋅ 3)] = 2(24 + 18 + 12) = 2(54) = 108 square units
The figures have the same surface area because they are made up of the same views.
Work Time
3-D Figures
- Sketch the 2-D views of the front, top, and side of Figure A. What do you notice?
- Sketch the 2-D views of the front, top, and side of Figure B. What do you notice?
- What is the surface area of each figure?
- Why do the two figures have the same surface area?
Hint:
- How do the opposite views of the figure compare?
- How can all of the surfaces be accounted for when finding the surface area of a figure?
3-D Figures
Possible Answers
- No answer; students will create 2-D views of the top, front, and right on grid paper.
- Answers will vary.
- Answers will vary.
- The surface area of the given figure is 162 square units: 24 + 24 + 22 + 22 + 25 + 25 + 20 = 162 units.
Work Time
3-D Figures
Open the 3-D Builder interactive and look at the given figure.
- Create 2-D views of the top, front, and right sides of the figure on grid paper.
- Build the views you drew on your grid paper in the 3-D Builder Interactive.
- Check to make sure that your 3-D figure is the same as in the interactive. If they aren't, fix your views.
- What is the surface area of the figure?
- Did you create all three 2-D views in the 3-D Builder interactive?
INTERACTIVE: 3-D Builder
Hint:
- How do the opposite views of the figure compare?
- How can all of the surfaces be accounted for when finding the surface area of a figure?
3-D Figures
Lesson Guide
Watch students interact with the 3-D figure with their partner.
Possible Answers
- Two-dimensional views will vary.
- Answers will vary.
- Calculations for surface area will vary.
- Answers will vary for partner work.
Work Time
3-D Figures
Create a 3-D figure for your partner using the Cube Building interactive.
- Have your partner create 2-D views of the top, front, and right of your figure.
- Reveal the 2-D views and check your partner’s work.
- Work together to calculate the surface area of the figure.
- Switch roles with your partner and repeat the activity.
INTERACTIVE: Cube Building
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who demonstrate the following strategies during the class discussion:
- Students who see that all of the surfaces are accounted for by the three views
- Students who explain what they learned about surface area of 3-D figures
Possible Answers
Presentations will vary.
Challenge Problem
Possible Answers
The method just used will work here. However, students need to be aware that for some figures, there can be “hidden” surfaces—surfaces that don’t show on the 2-D views. So, the surface area can be calculated using those views, but the four interior surfaces will need to be added in also.
This is one reason the 3-D view and the 2-D views are often shown together: to give the whole picture.
Work Time
Prepare a Presentation
Explain what you have learned regarding 3-D figures and calculating surface area. Use your work to support your explanation.
Challenge Problem
How would you find the surface area of this figure? How is it different from the other figures you have seen today?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How does the surface area for the left view surface area relate to the surface area of the right view of a 3-D object? What about the top and bottom views or the front and back views?
- Could you remove some cubes from the figures and still have the same surface area?
- Can two figures have the same surface area but a different volume?
- Can you think of a situation where the 2-D views would not show all of the surfaces? What would you do in that case?
- Could you use the 2-D views to find the volume of the figures?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- Why were the measurements in square units?
- How are the 2-D views similar to plans for a building?
- Is it necessary to have the 2-D and 3-D views of a figure?
ELL: As with other discussions, consider presenting some of the questions in writing to support ELLs. Further, consider providing sentence frames, such as the following (in the order the questions were given):
ELL: Be sure that your pace is appropriate, and if needed at any point, present the questions in writing. Consider that if the questions are shown in writing students can borrow some of the words from the questions to construct their answers. Provide sentence frames as appropriate.
- I found the formula for the surface area of a prism by…
- I could/could not remove some cubes from the figures and still have the same surface area because…
- Two figures can/cannot have the same surface area but different volume. That is because…
Performance Task
Ways of Thinking: Make Connections
- Take notes about your classmates’ methods for representing 3-D figures and calculating surface area.
Hint:
As your classmates present, ask questions such as:
- Could you remove some cubes from the figures and still have the same surface area?
- Can two figures have the same surface area but a different volume?
- Can you think of a situation in which the two-dimensional views would not show all the surfaces? What would you do in such a situation if you wanted to calculate the surface area of the figure?
- Could you use the two-dimensional views to find the volume of the figures?
- How are the two-dimensional views similar to plans for a building?
Surface Area
A Possible Summary
To have a complete and precise picture of a 3-D figure, it is necessary to see the 3-D and 2-D views. These views give all of the dimensions and show all of the surfaces. Like a rectangular prism, opposite sides are the same (in terms of the area of surface facing that direction). Because of this, the 2-D views can be used to find the surface area of solid figures.
Formative Assessment
Summary of the Math: Surface Area
- Write a summary about finding the surface area of 3-D figures using 2-D views.
Hint:
Check your summary.
- Do you describe how to find the surface area of solid figures that aren’t prisms?
- Do you explain what the two-dimensional views of the figure show?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for finding the surface areas of 3-D figures. If you notice insightful comments about how students find the surface areas of 3-D figures, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
A situation where I might want to find the surface area of a 3-D figure is …