Changing Scale

Overview
Students further explore scale, taking a scale drawing floor plan and redrawing it at a different scale.
Key Concepts
Students explore change from one scale to another, focusing on the ratios. Students will draw a scale model of a house.
Goals
- Redraw a scale drawing at a different scale.
- Find measurements using a scale drawing.
Glass House
Lesson Guide
Show students the Glass House and give them time to think about how they might estimate its length.
SWD: Students with disabilities, especially those with visual-spatial difficulties, may have difficulty assessing the estimated length of this house. Consider prompting students to compare the house to an object in the picture with a known size; this will encourage them to consider the relative length of the building.
Mathematics
Briefly discuss how students might estimate the size of the house. The purpose of showing the house in the Opening is to give students an idea of what the house looks like and a sense of its scale.
Ask students what other things in the image helps give an idea of how big the house is. The walls, the trees, even the size of cabinets can help establish scale. The walls in the house are actually 10.5 ft high, while most homes have 8-ft ceilings. The cabinets in the house are probably about 3 ft tall.
Opening
Glass House
This is the Glass House, designed and originally owned by Philip Johnson. It was completed in 1949 and is a landmark of modern architecture. Notice that there are no interior walls (except for the round structure that is a fireplace/bathroom).
- How long do you think the house is?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will redraw a scale drawing at a different scale.
Opening
Redraw a scale drawing at a different scale.
Redraw a Scale Drawing
Lesson Guide
Have students work with a partner. Allow students to struggle as they work out the measurements and transfer them to the grid. Students will have a sense of whether their drawing is accurate and will look for reasons why.
SWD: Consider providing some students with a version of the floor-plan image on a smaller grid. This visual support will help students visualize changes in scale more readily. You may also want to consider alternate ways of presenting this information (e g., visual supports, highlighting or bolding corresponding lengths to promote an understanding of the relationship between shapes, elements, and drawings).
Students with disabilities, especially those with visual spatial difficulties, may struggle to self-assess the accuracy of their drawings. It may be helpful to check in with students to provide coaching as they self-assess their drawings.
Consider identifying the most direct way of representing an accurate scale drawing and share this example with students who are struggling. Some students with disabilities may have more success with this task if they are taught one way of creating the drawing (versus many possible ways).
SWD: Allow students time to explain how they are doing what they are doing if it is not readily apparent when you observe.
ELL: In posing these questions, be sure that your pace is appropriate and that you are providing ample wait-time to allow for a thoughtful response. If needed at any point, present the questions in writing. Allow students to use dictionaries before responding if there are words in your question(s) that they don’t understand.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who have worked out a way to use the scale and redraw the floor plan accurately and can explain it.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who can justify the location of the objects within the house.
Mathematical Practice 5: Use appropriate tools strategically.
Look for students who use tools strategically.
Mathematical Practice 6: Attend to precision.
Students should see that most of the measurements are approximations due to the accuracy that they can measure. If students are “rounding” to the closest multiple of 2 ft, then they don’t have a clear understanding of a balance between approximation and precision.
Mathematical Practice 7: Look for and make use of structure.
Some students will break the wall dimension down by thirds (columns) and halves (doors).
Students can extend the natural grid of the house columns to give more reference points.
Interventions
Student has difficulty getting started.
- If each length on the floor plan is 2 ft, what length could you use to equal 2 ft on the centimeter grid?
- How many 2-ft lengths is the house in length and width?
- How can you locate everything inside that “box”?
Student has a solution.
- What are the dimensions of the bed? Do they make sense?
- What is the area of the house?
- How did you locate the columns and doors?
Student does not see that his or her drawing is not proportional to the image of the floor plan.
- How many lengths are there between the [ ] and the [ ]? For example: How many desk lengths are there between the desk and the bathroom?
- Is this also true for your drawing?
Possible Answers
- Students will redraw the floor plan of the Glass House. Most students will use 1 cm on the grid to equal 2 ft as the scale.
- The length of the house is 56 ft with 4 equally spaced columns. The distance between each column is .
- Many of the measurements will not be at 2-ft intervals. However, everything near the walls is about 2 ft from the wall. Measuring how far something inside the house is from the nearest outside wall is a critical measurement, as everything else will be based on it. Again, some students will choose one corner as a reference point.
- The center of the circle is also important because the rest of the interior is located relative to it.
Work Time
Redraw a Scale Drawing
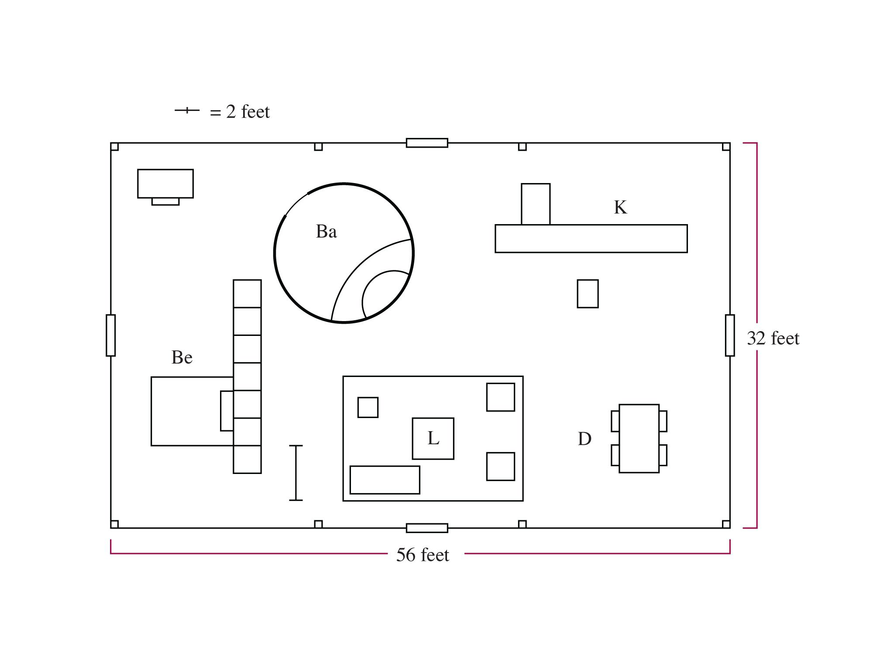
Here is the floor plan of the Glass House. The plan shows some furniture, such as a bed and dining table, as well as cabinets behind the bed and a kitchen counter.
Redraw the floor plan, including everything shown in the plan, on centimeter grid paper. Be aware that not all of the lines in the drawing will match to lines on the grid, but measure and draw as accurately as you can.
Follow these guidelines:
- Decide the scale you will use. What scale would be easiest?
- First locate the outside glass walls. These walls define the perimeter of the house (notice there are evenly spaced columns along the two longer sides). How much space is between each pair of columns?
- Locate something inside the house and measure how far it is from the nearest outside wall. For example: The desk in the upper-left corner is about 2 ft from each wall.
- To determine the size of the bathroom/fireplace, locate the center of the circle and draw a line to represent the radius.
Hint:
- Measure as accurately as you can. Notice that the 2-foot scale line at the top left of the floor plan has a line through the middle of it; this tells you that the segments on either side represent 1 foot.
- Locate each object by its vertical distance and horizontal distance from a corner.
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to be shared during class discussion:
- Students who use different scales to draw the floor plan (most students will probably use 1 cm = 2 ft, but some students may be able to use a length to equal 1 ft, which will probably result in a more accurate drawing)
- Students who use the same reference point for all measurements, similar to locating points on a coordinate plane
- Students who use the grid formed by columns to locate objects
- Students who realize that the columns are spaced in thirds along the walls and are directly across from each other, and that the doors are at the halfway point of each wall
Possible Answers
Presentations will vary.
- Most students will be able to tell if their drawing is proportional. They will sense where it is off, and most will understand that it was because of an inaccurate reading of the scale, or distance from other objects.
- Accuracy in measuring, especially if a distance was a whole number and a fraction of the scale length. Also translating that distance (for example, 7.5 ft) to the grid accurately.
- Answers will vary.
- The area of the actual house is 56 ft ⋅ 32 ft = 1,792 ft. Answers for students’ drawings will vary.
Challenge Problem
Possible Answers
The ratio of the house length to the house width is close to a 3:2 ratio, looking at the columns and doors. However, it is 56:32, which can be simplified to 7:4.
Work Time
Prepare a Presentation
- Does your drawing of the floor plan look like the original floor plan?
- What factors might have caused your drawing to look the same or different?
- Which measurements were the most difficult to make?
- What is the area of the actual house? What is the area of the house in your drawing?
Challenge Problem
- What is the ratio of the length of the house to its width?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How accurate do you think your results were? Why?
- How is the image on the screen different from the actual drawing or model?
- What strategies did you use to locate things accurately and make them the correct size?
- How did [names of two or three presenters] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- How could you measure more accurately?
- How many people live in the house? Why? Part of scale, and a discussion of architecture, is human scale: does the building “fit” people? Remember, the Pantheon is well above human scale and was built as a monument to the ancient Roman gods. Here, a house should be at a human scale. Clearly, one person lives here but could entertain people for dinner. With a 1,012 ft ceiling, nearly 1,800 ft2, and glass walls, the house would feel spacious, comfortable, and almost like being outside.
SWD: Consider showing these questions in writing and consider providing sentence frames such as the following:
“I think the results were…[very, somewhat, relatively, extremely]…accurate because…”
“The image on the screen is different from the actual drawing or model in that…”
“It shows…”
“[Name] organized his/her thoughts in the following way: He/she…”
“That makes sense to me because…” * “The structure of the mathematics was brought up by…”
Consider posting these sentence frames for reference for future lessons.
Performance Task
Ways of Thinking: Make Connections
Take notes about the approaches other students used to make their drawings.
Hint:
As your classmates present, ask questions such as:
- What is the scale of your drawing? Why did you choose that scale?
- How accurate do you think your drawing is? Explain.
- How do you think the image of the floor plan on your screen is different from the actual drawing?
- What strategies did you use to accurately locate things in the house and make them the correct size?
- How could you measure more accurately?
- How many people do you think live in the house? Justify your answer with data.
Scale Drawings
A Possible Summary
If scale drawings are redrawn at a different scale, they are still scaled and proportional to each other. Measuring accurately and transferring those measurements to the other drawing correctly is not easy to do. Still, using reference points and spacing things relative to each other it is possible to be accurate.
Formative Assessment
Summary of the Math: Scale Drawings
Write a summary about making a scale drawing from another scale drawing.
Hint:
Check your summary:
- Do you explain how your drawing and the original drawing are similar?
- Do you explain how to create a scale for your drawing based on the scale of the original drawing?
- Do you explain how to locate objects on the original drawing?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for redrawing a scale drawing using a different scale. If you notice insightful comments about how to redraw a scale drawing using a different scale, plan to share them with the class in the next lesson.
ELL: Be sure that ELLs have access to a dictionary and time to discuss with a partner before writing, to help them organize their thoughts. Allow ELLs who share the same primary language to discuss in their language of choice if they wish.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
A strategy I found useful in making my scale drawing is …