Calculating Volume

Overview
Students will extend their knowledge of volume to find the volume of right prisms, seeing that the volume is the area of the base multiplied by the height.
Key Concepts
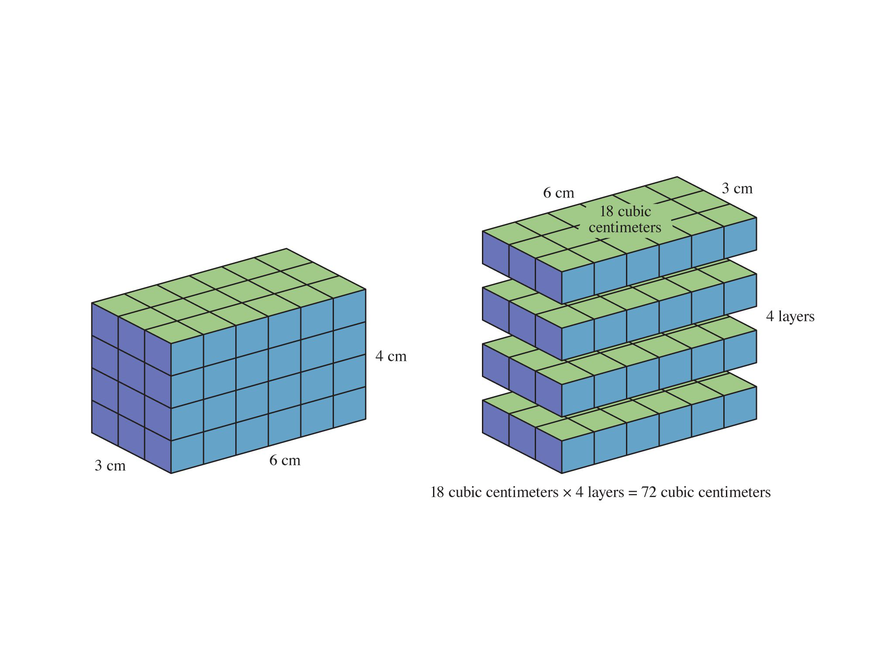
Volume is measured in cubic units. The area of the base of a prism indicates how many cubic units are in the first unit “layer” of the prism. Multiplying by height gives the number of layers, and therefore the volume.
Goals
- Find the volume of right prisms.
SWD: Some students with disabilities may have difficulty connecting newly introduced information with previously learned concepts. Consider ways to help students with disabilities to make connections between what they have learned in previous lessons about volume and right prisms and finding the volume of right prisms.
Consider the prerequisite skills for this lesson. Students with disabilities may need direct instruction and guided practice with the skills, measurement, and concepts needed for this lesson.
Students should understand these domain-specific terms:
- volume
- right (domain-specific)
- prism
- cubic
It may be helpful to preteach these terms to students with disabilities.
ELL: As new vocabulary is introduced, be sure to repeat it several times and allow students to repeat after you as needed. Write the new words as they are introduced, and allow enough time for ELLs to check their dictionaries or briefly consult with another student who shares the same primary language if they wish.
Volume of a Prism
Lesson Guide
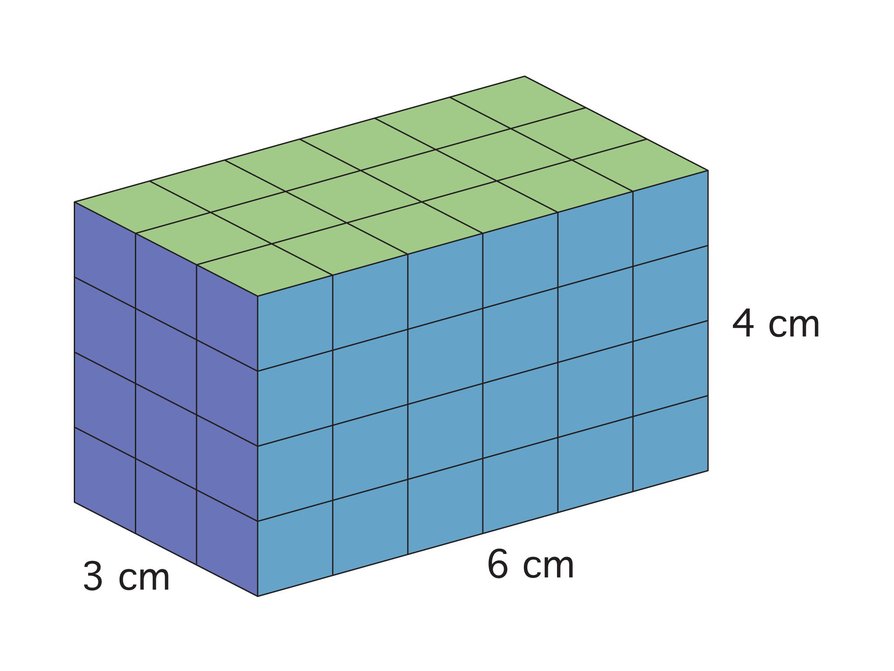
Show students the prism and discuss the question about its volume.
Mathematics
Briefly discuss the opening question, reviewing the volume formula for rectangular prisms. Remind students that volume measures how much space a figure takes up and is measured in cubic units.
Opening
Volume of a Prism
- What is the volume of this rectangular prism?
- Explain how you found the volume.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore and apply methods for finding the volume of a right prism.
Opening
Explore and apply methods for finding the volume of a right prism.
Find Volumes of Right Prisms
Lesson Guide
Have students work in groups. Give students time to struggle and discuss the problems with their group, but make sure that students have completed the problems and understand them before moving on.
Mathematics
Students need to see that the area of the base is the same number (different units) as the volume of the first layer of the prism. The area of the base indicates the volume of one layer of the prism, while the height tells the number of layers and therefore the volume. This understanding leads students to the conclusion that the shape of the base doesn’t matter, only that its area can be found. So the volume of a right prism is the area of the base (B = lw) multiplied by the height (V = Bh).
ELL: In forming groups, be aware of your ELLs and ensure that they have a learning environment where they can be productive. Sometimes, this means pairing them up with English speakers so they can learn from their language skills. Other times, it means pairing them up with students who are at the same level of language skills so they can take a more active role and work things out together. Or, pair them up with students whose proficiency level is lower so they play the role of the supporter. They can also be paired up based on their math proficiency.
ELL: Consider providing sentence frames to support ELLs with their answers. See examples below:
- For rectangular prisms, the length is multiplied by the width because….
- The volume would change to … if the height were 6 cm.
- I could find the volume by….
SWD: Students with disabilities may demonstrate difficulty initiating tasks. Some students may benefit from cues at the outset of independent and group work (proximal, visual, or verbal).
ELL: When eliciting answers, be cognizant of the difficulties some ELLs encounter. If you hear a student say the right thing using the wrong grammatical structure, show signs of agreement and softly rephrase using the correct grammar and the student’s words as much as possible. See the example below:
- The amount of units in the base is the same as the first layer…
Agree and rephrase: “The number of square units in the base is the same as the number of cubic units in the first layer of the prism.”
Consider saying the words in bold slowly, allowing students to repeat as appropriate.
Interventions
Student has difficulty getting started.
- For a rectangular prism, why is length multiplied by width?
- How does the area of the bottom layer compare to the volume of the bottom layer?
- If the height were 6 cm, how would the volume change?
Student does not see the relationship between area and volume.
- How can you find the number of squares (the area) in one layer of a prism?
- How can you find the number of cubes (the volume) in one layer of a prism?
Student has a solution.
- If the height of the prism were 6.43 cm, could you find the volume?
Student does not think that the volume of other prisms can be found the same way as a rectangular prism, because the base is not rectangular (resulting in square units).
- If the bottom of a rectangular prism were 4.5 cm long and 6.5 cm wide, could you find the area?
- Would all of the area be divided into whole squares?
- Do you know how to find the area of polygons?
- Are they made up of squares?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who work out the volume formula and understand why it works.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who see the relationship between the area of the base and volume for any prism and can generalize for all prisms.
Mathematical Practice 6: Attend to precision.
Look for students who label their answers with the correct cubic units for volume and square units for the base area.
Mathematical Practice 7: Look for and make use of structure.
Some students will make the connection between two-dimensional measurement and its application here—that the things they learned about finding the area of polygons, and scale, apply to finding the volume of a right prism.
Possible Answers
- The area of the bottom, or base, of the rectangular prism.
- The number of square units in the base is the same as the number of cubic units in the first layer of the prism. The volume of the first layer is the area multiplied by 1 cm, which does not change the number, but does change the unit from square to cubic.
- The height indicates the number of layers in the prism.
- The area of the base multiplied by the height is the volume, so it could be written as V = Bh, where B is the area of the base.
- The area of the base indicates the volume of the first layer, regardless of its shape, and the height still indicates the number of layers. So, to find the volume, the area of the base would still be multiplied by the height; the shape of the base doesn’t matter (as long as its area can be found).
Work Time
Find Volumes of Right Prisms
You know that you can find the volume of a rectangular prism by multiplying the length by the width by the height: V = lwh.
Carefully examine this drawing.
- What does the length multiplied by the width represent?
- How can you use your answer to the previous question to help you find the volume of the prism?
- What does the height represent?
- Rewrite the formula for the volume of a rectangular prism based on area.
- Suppose the shape of the base of the prism is not rectangular, but you know the area of the base (or how to find the area). How would you find the volume of the prism?
Hint:
What does the length times the width indicate in the picture?
Find Volumes of Right Prisms
Possible Answers
V = Bh
V = 15 ⋅ 6 = 90
The volume is 90 cm.
First the area of the base (B) must be found:
B = a()
B =
B =
B = 3(10.75) = 32.25
The area of the base is 32.25 cm.
Now the area of the base can be applied to the prism volume:
V = Bh
V = (32.25)(6) = 193.5
The volume of the prism is 193.5 cm.
Work Time
Find Volumes of Right Prisms
Thus, for any right prism, if you know the area of the base and the height, you can find the volume. The volume is equal to the area of the base, B, times the height:
V = Bh
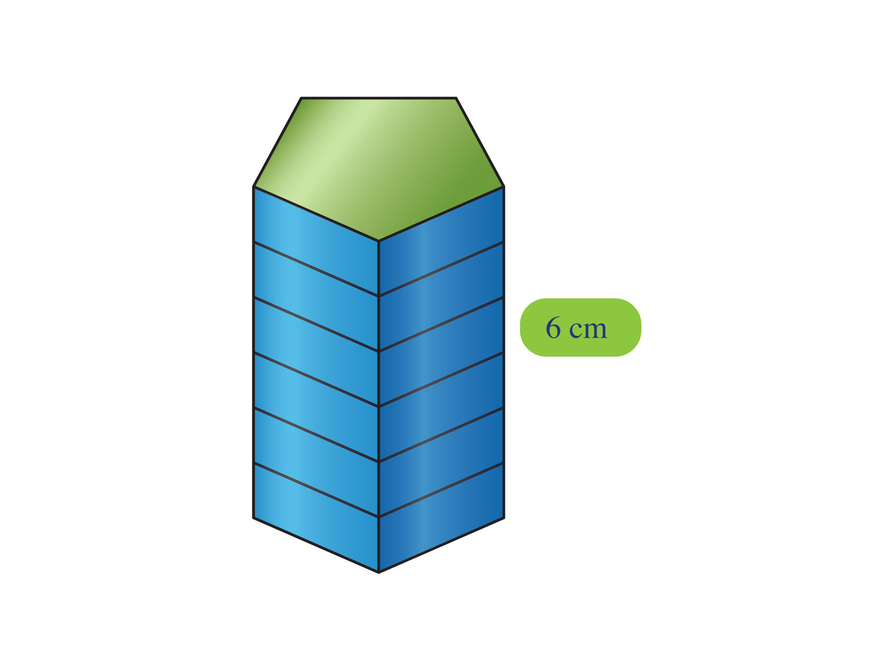
- If the area of the base of this regular pentagonal prism is 15 cm and the height is 6 cm, what is the volume of the prism?
- Suppose you do not know the area of the base, but you know that the apothem is 3 cm and the side lengths are 4.3 cm. Find the volume of the pentagonal prism.
Hint:
- If you know the area of the base and the height, how can you find the volume?
- How can you find the area of the base using the apothem and side length?
Find Volumes of Right Prisms
Possible Answers
Remembering to apply scale, the area of the base is .
V = Bh
V = 40 ⋅ 6 = 240 or 240 m
Again, using scale, the apothem is about 3.5 m, so the area of the base is about , or about 42 m.
V = Bh
V = 42 ⋅ 10 = 420, or 420 m
Work Time
Find Volumes of Right Prisms
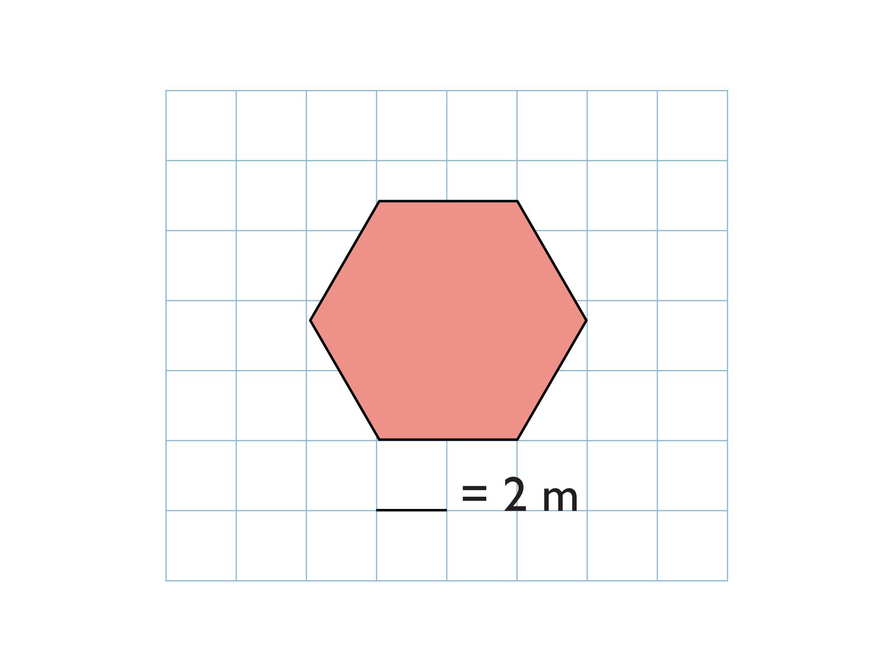
Each drawing shows the top view of a right prism.
- What is the volume of the triangular prism if the height of the prism is 6 m?
- What is the volume of the regular hexagonal prism if the height of the prism is 10 m?
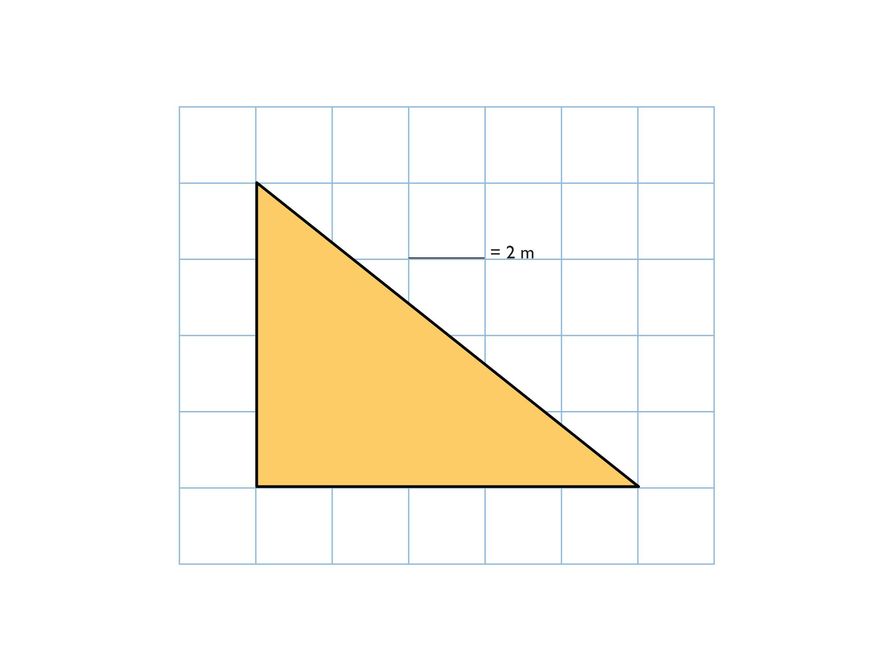
Hint:
- How can you use the scale to help you find the volume?
- How can you calculate the area of the base?
Prepare a Presentation
Preparing for Ways of Thinking
Look for the following strategies to share during class discussion. Look for students who do the following:
- See the relationship between the area of the bottom layer (the base) and the volume of one layer of the prism
- Understand that the height simply indicates the number of layers or multiples of the bottom layer’s volume
- Understand that the area of the bottom layer (or base) is the key to finding the volume and that length multiplied by width happens to be the area for the base of rectangular prisms
Answer
Presentations will vary.
Challenge Problem
Possible Answers
- The height is 4 in.
V = Bh
120 = 30 ⋅ h
= h
4 = h
Work Time
Prepare a Presentation
Explain what you know about finding the volume of a right prism. Use examples of your work to illustrate your explanation.
Challenge Problem
- If the volume of a prism is 120 in. and the area of the base is 30 in., what is the height of the prism?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How did you find the formula for the volume of a prism?
- How was the formula similar to the formula for the volume of a rectangular prism?
- How do the numbers for volume compare to the numbers for area? (Answer: The numbers are generally greater for volume, because three numbers are multiplied together instead of two.)
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- Why were the measurements in cubic units?
SWD: For students with language based learning vulnerabilities or learning challenges, participating in a whole-class discussion such as Ways of Thinking can be intimidating for a variety of reasons. However, it is important for students to work on the speaking and listening skills implicit to this portion of the lesson. Possible supports for students prior to and during this portion of the lesson include:
- Giving students a few minutes to discuss their ideas, the questions posed, and what has taken place during the lesson with a partner or small group before sharing in the whole-class setting.
- Conferencing with individual students prior to the discussion to ascertain what they might be able to successfully contribute to the discussion. Encourage students to rehearse their contribution or to write notes for themselves to refer to when they speak. This will support students with expressive language difficulties and/or students who are anxious or reluctant to participate in class discussions.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ explanations for finding the volume of a right prism.
Hint:
As your classmates present, ask questions such as:
- Can you explain the steps you used to rewrite the formula based on area?
- How is the formula that you wrote based on area similar to the original formula?
- How do the values for volume compare to the values for area?
- Why are the units for volume cubic units?
- How can you apply your strategy for finding the volume of a right prism to other right prisms with bases of various shape and size?
Volume of Right Prisms
A Possible Summary
- The volume of a rectangular prism is found by multiplying the area of the base (length • width) by the height. The area of the base indicates the volume of the first unit layer of the prism and is multiplied by the height for the number of layers. As long as the area of the base can be found, its shape doesn’t matter and can be multiplied by the height. The volume for any right prism is V = Bh where B is the area of the base.
Formative Assessment
Summary of the Math: Volume of Right Prisms
Write a summary about finding the volume of a right prism.
Hint:
Check your summary:
- Do you explain how the area of the base of a prism relates to the volume of the prism?
- Do you explain how the height of a prism relates to the volume of the prism?
- Do you provide two formulas for finding the volume of a right prism, and explain each formula?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for finding the volume of a right prism. If you notice insightful comments about how students explored and applied methods to find the volume of a right prism, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something else I would like to know about prisms is …