- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Surface Area Of Prisms

Overview
Students will extend their knowledge of surface area and nets of rectangular prisms to generalize a formula for the surface area of any prism.
Key Concepts
Students know how to find the surface area of a rectangular prism using a net and adding the areas for pairs of congruent faces. Students have not seen that the lateral surface forms one long rectangle whose length is the perimeter of the base and whose width is the height of the prism.
Using this idea, the surface area of any right prism can be found using the formula:
SA = 2B + (perimeter of the base)h
Goals
- Find a general formula for surface area of prisms.
- Find the surface area of different prisms.
SWD: Generalization of skills can be particularly challenging for some students with disabilities. Students may need direct instruction on the connection between what they already understand and a general formula.
Some students with disabilities may have difficulty recalling formulas when it comes time to apply them. Once students discover the formula SA = 2B + (perimeter of the base)h, consider posting the formula in the classroom and encouraging students to add the formula(s) to the resources they have available when completing classwork and homework.
Surface Area of a Prism
Lesson Guide
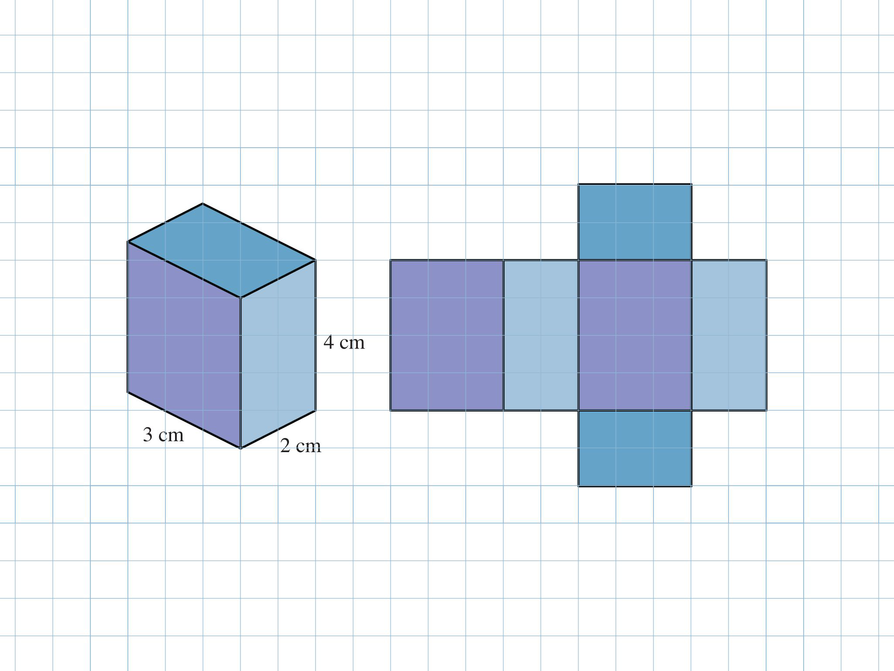
Show students the rectangular prism and its net and discuss the question about its surface area.
SWD: Some students with disabilities may struggle to connect 2-D representations with 3-D shapes. It may be helpful to provide students with physical manipulatives to compare to 2-D representations of the shapes and nets.
Mathematics
Briefly discuss the opening question. Students know that they can find the surface area of the prism by adding up the area of each face. Students also know that the faces that are opposite each other in the prism are congruent: the prism consists of three pairs of faces.
Remind students that the top and bottom faces are called bases and that the vertical faces are called lateral faces.
Opening
Surface Area of a Prism
- What is the surface area of this rectangular prism?
- Explain how you found the surface area.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore and apply the method for finding the surface area of a right prism.
Opening
Explore and apply the method for finding the surface area of a right prism.
Find Surface Area Using Nets
Lesson Guide
Have students work in groups. Give students time to work through and discuss the problems with their group, but make sure that students have completed the first problem and understand it before moving on.
Mathematics
Students need to see that the rectangular area of the lateral surface is found by multiplying the length (the perimeter of the base) by the width (the height of the prism). That area plus the area of the bases is the surface area of the prism.
SWD: Students with disabilities may not as readily recognize relationships between measurements. It may be helpful to instruct students on the nature of these relationships, perhaps color-coding related measures of the surfaces to promote understanding.
ELL: Ask some questions to all students, but especially to ELLs, to check for understanding before moving on.
ELL: When eliciting answers, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a foreign language. For example, if you hear them say the right things but use the wrong grammatical structure, show signs of agreement and softly rephrase using the correct grammar and the student’s words as much as possible.
For example, if a student says: “The base is the same as the side,” rephrase by saying “The perimeter of the base is the same as the length of the lateral surface.” Ask the student to repeat and check for understanding. Follow a similar process for the other questions.
Students will begin to see how this formula applies to any right prism as they work through the tasks.
Interventions
Student has trouble seeing the relationship between the perimeter of the base and the area of the lateral surface.
- What lengths make up the base’s perimeter?
- Where else do you see these lengths?
- If the base could roll along the length of the lateral surface, what would that look like?
- What shape is the lateral surface?
- How do you find its area?
Student has a solution.
- If the height of the prism were 6.43 cm, could you find the surface area?
- Does the shape of the base matter?
- What do you need to know about the base?
Student does not think that the surface area of other prisms can be found the same way as a rectangular prism because the base is not rectangular.
- Draw the net for the prism.
- What is the width of the lateral faces?
- What is the length?
- What is the perimeter of the base?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who work out the surface area formula and understand why it works.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who see the relationship between the perimeter of the base and the lateral surface area for any prism and can generalize for all prisms.
Mathematical Practice 6: Attend to precision.
Look for students who label their answers with the correct square units for the surface area.
Mathematical Practice 7: Look for and make use of structure.
Some students will make the connection between 2-D measurement and 3-D measurement—that the same one-dimensional measurements are used to find the other measures in prisms. These students will also begin to suspect that there is a relationship between volume and surface area.
Possible Answers
Answers will vary. If students understand how to draw the net and how side lengths are related, they may see the connection.
- The perimeter of the base is the same as the length of the lateral surface.
- Each lateral face shares its top edge with a side of the base, so the total length of the lateral surface is the same length as the perimeter of the base.
- Multiply the perimeter of the base by the height of the prism to find the area of the lateral surface.
- Find the lateral surface area by multiplying the perimeter of the base by the height of the prism. Then add twice the area of the base.
Work Time
Find Surface Area Using Nets
The top and bottom faces of a prism are the bases. The remaining faces are the lateral faces. Notice that the lateral faces form one large rectangle. This rectangle is called the lateral surface.
Use the Prism Net interactive to explore the net of a rectangular prism. Notice that as you change the net, the faces of the prism adjust accordingly.
- How do you think the perimeter of the base and the length of the lateral surface are related?
- Why do you think the perimeter of the base and the length of the lateral surface are related in this way?
- How could you find the area of the lateral surface?
- Based on your observations about lateral surface area, describe a method for finding the surface area of a rectangular prism.
INTERACTIVE: Prism Net
Hint:
- What are the width and length of the lateral surface, and how could you use those measurements to find the area of the lateral surface?
Find Surface Area Using Nets
Possible Answers
- 10 units long, 3 units wide
First find the lateral surface area by multiplying the lateral length by the lateral width found in the first check mark. Then add twice the area of the pentagon base (the apothem would need to be known):
Lateral Surface Area: lw = 10 ⋅ 3 = 30
Area of Pentagon Base(s): is about 1.38() = 6.9
Total Surface Area: Lateral Surface Area + 2(Area of Base) = 30 + 2(6.9) = 43.8 or 43.8 units
Note: Students may estimate the apothem to be about 1.5 units by noticing that the pentagon is 3 units high. This would make the area of the pentagon base
1.5() = 7.5, which means the total area would be 30 + 2(7.5) = 45 or 45 units.- Answers will vary.
Work Time
Find Surface Area Using Nets
Find the surface area of this regular pentagonal prism.
- How long is the lateral surface? How wide is the lateral surface?
- Use this information to find the surface area of the prism.
- Explain the steps you used.
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who demonstrate the following strategies to be shared during the class discussion:
- Students who see the relationship between the perimeter of the base and the lateral surface
- Students who make the connection between surface area for rectangular prisms and other prisms, seeing that the lateral surface is always a rectangle with a length of the base’s perimeter and a width the height of the prism
- Students who see the connection to volume (the shape of the base is irrelevant, as long as its measurements are known)
Possible Answers
Presentations will vary.
Challenge Problem
Answers
The volume of a prism is going to be the area of the base multiplied by the height of the prism. Since the volume is 48 ft and the height is 3 ft, we can say the area of the base is x.
Volume = area of base ⋅ height of the prism
48 = (x2) ⋅ 3
16 = x2
x = 4 ft
Now to find the surface area of the prism, we need to get the lateral surface area and add the area of the two bases.
Lateral surface area:
(4 + 4 + 4 + 4) ⋅ 3 = 48 ft
Area of the bases:
2(4 ⋅ 4) = 32 ft
Total surface area:
48 ft + 32 ft = 80 ft
Work Time
Prepare a Presentation
Describe how to find the surface area of a right prism. Support your thinking with examples.
Challenge Problem
A square prism has a height of 3 ft and a volume of 48 ft. What is the total surface area of the prism?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson, making sure to address any questions students have from their work. Ask questions such as these:
- How did you find the formula for the surface area of a prism?
- How was the formula similar to the formula for the surface area of a rectangular prism?
- How do you think volume and surface area are related?
- How did [student names] organize their thoughts differently? Which way of thinking makes more sense to you? Which way of thinking brought out the structure of the mathematics?
- How did [student names] make sense of the problem?
- Could you state what [student names] said in a different way?
- Why were the measurements in square units?
- Can you think of situations where the total surface area would be needed and where only the lateral surface area would be needed?
ELL: Consider providing some sentence frames for the discussion such as these:
- The formula I found is…
- I found the formula by…
- I organized my thoughts in the following way…
- This way of thinking makes sense to me because…
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ explanations for finding the surface area of a right prism.
Hint:
As your classmates present, ask questions such as:
- How did you find the formula for the surface area of a prism?
- How is the formula similar to the formula for the surface area of a rectangular prism?
- How do you think volume and surface area of a right prism are related?
Find the Surface Area from the Base
Answers
- The perimeter of the base is 12 cm.
4 cm + 4 cm + 4 cm = 12 cm
Area of Bases
Lateral Surface Area 12 cm ⋅ 10 cm = 120 cm
Total Surface Area: 13.84 cm2 + 120 cm2 = 133.84 cm
The surface area is about 134 cm.
- The perimeter of the base is 26 cm.
2(5 cm + 3 cm + 5 cm) = 26 cm
The base can be arranged into a parallelogram with a base of 14 cm and a height of 3 cm.
Area of Bases: 2(14 cm ⋅ 3 cm) = 84 cm
Lateral Surface Area: 26 cm ⋅ 5 cm = 130 cm
Total Surface Area: 84 cm + 130 cm = 214 cm
Work Time
Find the Surface Area From the Base
Each drawing shows the base of a prism. Find the surface area of each prism using the information in the drawings and the height information that follows. Draw the net of each prism first.
- The triangular prism has a height of 10 cm.
- The hexagonal prism has a height of 5 cm.

Hint:
- What does the perimeter of the base indicate about the lateral surface?
- What do all right prisms have in common in terms of describing the surface area?
Surface Area of Right Prisms
A Possible Summary
The lateral faces of a rectangular prism form a long rectangle. The length of the rectangle is the same as the perimeter of the base, and the width is the same as the height of the prism. So, the lateral surface area can be found by multiplying these two numbers. Then the area of the bases can be added for the total surface area. This same procedure applies for all right prisms.
SWD: As in other lessons, when academic language is reviewed (or introduced, for that matter) consider showing it in writing and leaving it in a place that is visible so that all students can refer to it.
Formative Assessment
Summary of the Math: Surface Area of Right Prisms
Write a summary about finding the surface area of a right prism.
Hint:
Check your summary.
- Do you describe how the perimeter of the base is related to the lateral surface of a prism?
- Do you explain the method for finding the surface area of a prism?
- Do you provide the formula for the surface area of a right prism, and explain what it means?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to see students’ strategies for finding the surface area of a right prism. If you notice insightful comments about how students find the surface area of a right prism, plan to share them with the class in the next lesson.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One way I can figure out the surface area of a right prism is …